[笔记]树套树 之 树状数组套权值线段树
前
树状数组套权值线段树,是众多树套树的一种(下文树套树默认指树状数组套权值线段树),可以在单次查询 / 点修均 \(O(\log^2 n)\) 的时间复杂度内,在线处理二维数点 / 区间第 \(k\) 小等问题。
- 前置知识:
- 线段树
- 树状数组
- 可持久化线段树
- 本文代码中
auto [a,b,c]=q[i]的写法仅c++17及以上可用,请勿在 NOIp 等考场上使用 ><
upd on 2025/10/17:经了解,因为 c++14 会向后兼容,所以应该是可以使用的,只是会报警告。
思路简述
后面会有对应的例题。
二维偏序
二维偏序问题,即在一个由 \(n\) 个二元组构成的集合 \(\{(x_1,y_1),\dots,(x_n,y_n)\}\) 中,求与 \((x_i,y_i)\) 满足某种偏序关系,即 \((x_i,y_i)\prec(x_j,y_j)\) 的 \(j\) 的个数。
这其中,“\(\prec\)”是一种具有自反性、反对称性、传递性的二元关系,例如:
- \(x_i\le x_j,\ y_i<y_j\)
- \(x_i>x_j,\ y_i\le y_j\)
- \(\dots\)
逆序对就是常见的二维偏序问题,此时这个集合可以写为 \(\{(1,a_1),\dots,(n,a_n)\}\)。
我们先考虑下面的问题:
对于一个长度为 \(n\) 的序列 \(A\),你需要回答若干个询问:
- 求下标在 \([l,r]\) 范围内,值域在 \([a,b]\) 范围内的元素个数。
若操作离线,我们可以使用主席树。用前缀和的思想,令第 \(i\) 棵权值线段树存储 \(A_{1\sim i}\) 的数据。查询时用第 \(r\) 和第 \(l-1\) 棵线段树作差,在这棵新的线段树上查询 \([a,b]\) 区间和即可。
若强制在线,我们类比序列上的操作,将前缀和改为树状数组来维护,每个树状数组的节点都是一棵线段树,这棵线段树就是其管辖范围内所有线段树的和。
修改和查询和普通树状数组完全一样,只不过是数值的操作变成了对线段树的操作。即:
- 修改时最多修改 \(\log n\) 棵线段树。
- 用于查询的 \([l,r]\) 区间的线段树,可以表示为最多 \(\log V\) 棵线段树与最多 \(\log V\) 棵线段树作差的形式。
外层树状数组操作是 \(O(\log n)\),内层权值线段树是 \(O(\log V)\),其中 \(V\) 为值域。于是我们可以达到修改、查询均为 \(O(\log n\log V)\) 的时间复杂度。
为了让空间不炸,我们选择动态开点的权值线段树。线段树用去的节点数量上界是 \(n\log n\log V\)(实际情况远小于上界)。
在 \(V\) 较大时,我们常常先对值域离散化,这样上文的 \(\log V\) 会降为 \(\log n\)。
这就是树套树的基本框架。
struct SEG{//权值线段树
int idx;
struct node{int lc,rc,sum;}tr[N*logN*logV];//这个要视情况而定
#define lc(x) (tr[x].lc)//请注意,不使用undef的话,define的作用域是从此处直到文件结尾
#define rc(x) (tr[x].rc)//放在这里面只是为了条理一些
#define sum(x) (tr[x].sum)//也可以使用内联函数(inline)来解决这个问题
void chp(int &x,int a,int v,int l,int r){
if(!x) x=++idx;//动态开点
sum(x)+=v;
if(l==r) return;
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
}
int query(int x,int a,int b,int l,int r){
if(a<=l&&r<=b) return sum(x);
int mid=(l+r)>>1,ans=0;
if(a<=mid) ans+=query(lc(x),a,b,l,mid);
if(b>mid) ans+=query(rc(x),a,b,mid+1,r);
return ans;
}
}tr;
struct BIT{//树状数组
void chp(int x,int a,int v){//第x棵线段树的第a位累加v
while(x<=n) tr.chp(root[x],a,v,1,n),x+=lowbit(x);
}
int query(int x,int a,int b){//[1,x]线段树在[a,b]上的和
int ans=0;
while(x) ans+=tr.query(root[x],a,b,1,n),x-=lowbit(x);
return ans;
}
}bit;
进而我们就可以很轻松地解决二维偏序问题,令外层树状数组维护下标,内层线段树维护值域。统计答案时按上面的问题查询即可。
树状数组上的查询依赖于数据的可加减性,因此树状数组套权值线段树所维护的内容一般需要是可加减的(比如区间和,但区间最值不是);如果想维护区间最值之类,可以将外层的树状数组换成线段树。
二维数点
二维数点,即在二维平面上给出若干点,然后进行若干次查询,每次询问某个矩形中有多少个点。
形式化地,即:有 \(n\) 个二元组 \((x_1,y_1),\dots,(x_n,y_n)\),每次询问给定 \(a,b,c,d\),求满足 \(x_i\in [a,b],y_i\in [c,d]\) 的 \(i\) 有多少个。
离散化一下就可以用上面的方法来解决了,外层树状数组维护 \(x\),内层线段树维护 \(y\)。
三维偏序
相较二维偏序多了一维,变成 \((x,y,z)\)。
能在线求二维偏序,就能离线求三维偏序。拿 \(x_i\le x_j,y_i\le y_j,z_i\le z_j\) 为例。
我们将所有点离线下来排序,按 \(x\) 从小到大遍历,并将 \((y,z)\) 放入树套树,以保证查询 \((x,y,z)\) 时,有且仅有满足 \(x'\le x\) 的 \((x',y',z')\) 被放入树套树即可。这样第一维 \(x\) 解决,剩下的就是 \(y,z\) 的二维偏序了,直接搬上面的代码即可。
三维数点
三维坐标系中的数点。
形式化地,即:有 \(n\) 个三元组 \((x_1,y_1,z_1),\dots,(x_n,y_n,z_n)\),每次询问给定 \(a,b,c,d,e,f\),求满足 \(x_i\in [a,b],y_i\in [c,d],z_i\in [e,f]\) 的 \(i\) 有多少个。
仍然将操作离线。\(x\in [a,b]\) 的答案,可以拆成两次查询,即 \(x\in [1,b]\) 和 \(x\in [1,a-1]\) 的答案作差。
也就是说,我们仍然将所有点按 \(x\) 从小到大排序,并在遍历过程中将 \((y,z)\) 放入树套树。这样第一维 \(x\) 解决掉。
当 \(x\in[1,w]\) 的点添加完毕后,则根据我们的查询内容,对 \(y,z\) 进行二维数点,对答案进行累加 / 累减。
例题
P3157 [CQOI2011] 动态逆序对
树套树基本操作的例题。
不难发现,每删除 \(1\) 个元素 \(v\),就将答案减去“\(v\) 左边比 \(v\) 小的元素个数”和“\(v\) 右边比 \(v\) 大的元素个数”。
查询它们,直接套上面的代码就可以。
时间复杂度 \(O((n+m)\log^2 n)\)。
节点总数 \(n \log^2 n\)。
点击查看代码 R223054208
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
int n,q,a[N],pos[N],root[N],ans;
inline int lowbit(int x){return x&-x;}
struct SEG{
int idx;
struct node{int lc,rc,sum;}tr[N*18*18];
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define sum(x) (tr[x].sum)
void chp(int &x,int a,int v,int l,int r){
if(!x) x=++idx;
sum(x)+=v;
if(l==r) return;
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
}
int query(int x,int a,int b,int l,int r){
if(a<=l&&r<=b) return sum(x);
int mid=(l+r)>>1,ans=0;
if(a<=mid) ans+=query(lc(x),a,b,l,mid);
if(b>mid) ans+=query(rc(x),a,b,mid+1,r);
return ans;
}
}tr;
struct BIT{
void chp(int x,int a,int v){
while(x<=n) tr.chp(root[x],a,v,1,n),x+=lowbit(x);
}
int query(int x,int a,int b){//[1,x]线段树在[a,b]上的和
int ans=0;
while(x) ans+=tr.query(root[x],a,b,1,n),x-=lowbit(x);
return ans;
}
}bit;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>q;
for(int i=1;i<=n;i++){
cin>>a[i],pos[a[i]]=i;
ans+=bit.query(i-1,a[i],n);
bit.chp(i,a[i],1);//本应该是a[i]+1,但a[i]互不相同所以没关系,况且边界处理稍麻烦
}
int v,p;
while(q--){
cin>>v,p=pos[v];
cout<<ans<<"\n";
bit.chp(p,v,-1);
ans-=bit.query(p-1,v,n);//同理
ans-=bit.query(n,1,v)-bit.query(p-1,1,v);
}
return 0;
}
与此同理的还有 P1975 [国家集训队] 排队和它的加强版 P12685 [国家集训队] 排队 加强版。
后面那道我已经尽力卡常了(哭)
以下是随机数据下的运行情况:
很奇怪,为什么跑得比题解快还会 T,难道洛谷数据不是随机的吗?过几天再探究下原因,并会将 AC 代码放上来。
此问题也发在讨论区,欢迎分享你的见解。
P3810 【模板】三维偏序(陌上花开)
三维偏序例题。
时间复杂度 \(O(n\log n\log k)\)。也可以离散化做到 \(O(n\log^2 n)\),不过因为 \(k\) 比 \(n\) 大不了多少,所以没有必要。
节点总数 \(n\log n\log k\)。
点击查看代码 R223063850
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,K=2e5+10;
int n,k,root[K],ans[N];
inline int lowbit(int x){return x&-x;}
struct node{int a,b,c;}a[N];
struct SEG{
int idx;
struct node{int lc,rc,sum;}tr[N*18*18];
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define sum(x) (tr[x].sum)
void chp(int &x,int a,int v,int l,int r){
if(!x) x=++idx;
sum(x)+=v;
if(l==r) return;
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
}
int query(int x,int a,int b,int l,int r){
if(a<=l&&r<=b) return sum(x);
int mid=(l+r)>>1,ans=0;
if(a<=mid) ans+=query(lc(x),a,b,l,mid);
if(b>mid) ans+=query(rc(x),a,b,mid+1,r);
return ans;
}
}tr;
struct BIT{
void chp(int x,int a,int v){
while(x<=k) tr.chp(root[x],a,v,1,k),x+=lowbit(x);
}
int query(int x,int a,int b){
int ans=0;
while(x) ans+=tr.query(root[x],a,b,1,k),x-=lowbit(x);
return ans;
}
}bit;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>k;
for(int i=1;i<=n;i++) cin>>a[i].a>>a[i].b>>a[i].c;
sort(a+1,a+1+n,[](node a,node b){return a.a<b.a;});
int last=1;
for(int i=1;i<=n;i++){
bit.chp(a[i].b,a[i].c,1);
if(a[i].a!=a[i+1].a){
while(last<=i){
ans[bit.query(a[last].b,1,a[last].c)-1]++;
last++;
}
}
}
for(int i=0;i<n;i++) cout<<ans[i]<<"\n";
return 0;
}
CF848C Goodbye Souvenir
二维数点例题。
“每种颜色最右边 \(-\) 最左边求和”看起来不好直接维护,但是可以转化为“相邻同色位置的下标差求和”。
也就是说,如果令 \(pre_i\) 表示最大的 \(j<i\) 使得 \(a_j=a_i\)(不存在为 \(0\)),那么 \([l,r]\) 的答案就是:
如果将 \((i,pre_i)\) 看作二维平面上的点,\(i-pre_{i}\) 看作点权,那么我们要统计的实际上是一个矩形区域内的点权和。因此这是一个二维数点问题。
可以用外层树状数组维护第一维,内层线段树维护第二维。
单点修改时,受到影响的只可能有:
- 被修改的位置。
- 与旧颜色相同的后一位。
- 与新颜色相同的后一位。
可以使用 set 很方便地维护这些位置信息。
需要注意的是,如果你使用节点回收,那么需要特判 \(a_x=y\) 的情况,否则可能会 WA on #6。
这是因为如果 \(a_x=y\),在处理中途线段树上可能出现负数,而节点回收条件是 sum(x)=0,所以可能会在子节点的 \(sum\neq 0\) 的情况下将 \(sum=0\) 的父节点错误地回收掉。
解决方法就是加上特判 / 不使用节点回收。
下面的样例的答案应为 9 9,可用于验证。
6 3
1 2 3 1 3 2
2 1 6
1 2 2
2 1 6
点击查看代码 #329304500
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10,V=1e5+10;
int n,m,root[N],a[N];
set<int> p[V];
inline int lb(int x){return x&-x;}
struct SEG{
stack<int> gar;
int idx,lc[120*N],rc[120*N];ll sum[120*N];
void del(int &x){gar.push(x),x=0;}
void newnode(int &x){
if(!gar.empty()) x=gar.top(),gar.pop(),lc[x]=rc[x]=sum[x]=0;
else x=++idx;
}
void chp(int &x,int a,int v,int l,int r){
if(!x) newnode(x);
sum[x]+=v;
if(l<r){
int mid=(l+r)>>1;
if(a<=mid) chp(lc[x],a,v,l,mid);
else chp(rc[x],a,v,mid+1,r);
}
if(!sum[x]) del(x);
}
ll query(int x,int a,int b,int l,int r){
if(a<=l&&r<=b) return sum[x];
int mid=(l+r)>>1;ll ans=0;
if(a<=mid) ans+=query(lc[x],a,b,l,mid);
if(b>mid) ans+=query(rc[x],a,b,mid+1,r);
return ans;
}
}seg;
struct BIT{
void chp(int x,int ia,int iv){
for(;x<=n;x+=lb(x)) seg.chp(root[x],ia,iv,0,n);
}
ll query(int x,int ia,int ib){
ll ans=0;
for(;x;x-=lb(x)) ans+=seg.query(root[x],ia,ib,0,n);
return ans;
}
}bit;
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1,pre;i<=n;i++){
cin>>a[i];
pre=p[a[i]].empty()?0:(*p[a[i]].rbegin());
bit.chp(i,pre,i-pre);
p[a[i]].insert(i);
}
int op,x,y,pre,nxt;
set<int>::iterator it;
while(m--){
cin>>op>>x>>y;
if(op==1){
if(a[x]==y) continue;
p[a[x]].erase(x);
it=p[y].lower_bound(x+1),pre=0;//1.与新颜色相同的后一位
if(it!=p[y].begin()) pre=*(--it);
it=p[y].upper_bound(x);
if(it!=p[y].end()){
nxt=*it;
bit.chp(nxt,x,nxt-x);
bit.chp(nxt,pre,pre-nxt);
}
it=p[a[x]].lower_bound(x+1),pre=0;//2.与旧颜色相同的后一位
if(it!=p[a[x]].begin()) pre=*(--it);
it=p[a[x]].upper_bound(x);
if(it!=p[a[x]].end()){
nxt=*it;
bit.chp(nxt,x,x-nxt);
bit.chp(nxt,pre,nxt-pre);
}
bit.chp(x,pre,pre-x);//3.被修改的位置
a[x]=y,pre=0;
it=p[y].lower_bound(x+1);
if(it!=p[y].begin()) pre=*(--it);
p[y].insert(x);
bit.chp(x,pre,x-pre);
}else{
cout<<bit.query(y,x,n)<<"\n";
}
}
return 0;
}
P3759 [TJOI2017] 不勤劳的图书管理员
题面太抽象了,人话就是要维护序列 \(a,v\),需要支持 \(x\) 与 \(y\) 位交换,并支持查询:
动态逆序对的加强版,现在是带权的。
这样我们需要在线段树上维护两个值,一个是个数,一个是权值和。
查询时需要将所有满足 \(i<j\) 且 \(a_i>a_j\) 的 \(j\) 在线段树上求出权值和,再加上总个数 \(\times v_i\) 即可。
点击查看代码 R225456803
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e4+10,V=1e5+1,P=1e9+7;
int n,m,a[N],v[N],root[N];ll ans;
struct Data{
int cnt;ll sum;
Data operator+(const Data& b) const{return {cnt+b.cnt,sum+b.sum};}
Data operator-(const Data& b) const{return {cnt-b.cnt,sum-b.sum};}
};
struct SEG{
int idx,lc[200*N],rc[200*N];
Data d[200*N];
void chp(int& x,int a,Data v,int l,int r){
if(!x) x=++idx;
d[x]=d[x]+v;
if(l==r) return;
int mid=(l+r)>>1;
if(a<=mid) chp(lc[x],a,v,l,mid);
else chp(rc[x],a,v,mid+1,r);
}
Data query(int x,int a,int b,int l,int r){
if(a<=l&&r<=b) return d[x];
int mid=(l+r)>>1;Data ans{0,0};
if(a<=mid) ans=ans+query(lc[x],a,b,l,mid);
if(b>mid) ans=ans+query(rc[x],a,b,mid+1,r);
return ans;
}
}seg;
inline int lb(int x){return x&-x;}
struct BIT{
void chp(int x,int ia,Data iv){
for(;x<=n;x+=lb(x)) seg.chp(root[x],ia,iv,0,V);
}
Data query(int x,int ia,int ib){
Data ans{0,0};
for(;x;x-=lb(x)) ans=ans+seg.query(root[x],ia,ib,0,V);
return ans;
}
Data query(int x,int y,int ia,int ib){
return query(y,ia,ib)-query(x-1,ia,ib);
}
}bit;
ll calc(int x,int y,int ia,int ib,int v){
Data d=bit.query(x,y,ia,ib);
return 1ll*d.cnt*v+d.sum;
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i]>>v[i];
ans+=calc(1,i-1,a[i]+1,V,v[i]);//这里如果按i离线,额外开一个树状数组会更快些
bit.chp(i,a[i],{1,v[i]});
}
while(m--){
int x,y;
cin>>x>>y;
if(x>y) swap(x,y);
ans+=calc(x,y,a[x]+1,V,v[x]);
ans-=calc(x,y,0,a[x]-1,v[x]);
ans-=calc(x,y,a[y]+1,V,v[y]);
ans+=calc(x,y,0,a[y]-1,v[y]);
if(a[x]<a[y]) ans-=v[x]+v[y];
else if(a[x]>a[y]) ans+=v[x]+v[y];
bit.chp(x,a[x],{-1,-v[x]});
bit.chp(y,a[y],{-1,-v[y]});
swap(a[x],a[y]),swap(v[x],v[y]);
bit.chp(x,a[x],{1,v[x]});
bit.chp(y,a[y],{1,v[y]});
cout<<ans%P<<"\n";
}
return 0;
}
P4396 [AHOI2013] 作业
二维 & 三维数点例题。
第一问是裸的二维数点。
第二问考虑转化一下,与上题类似地,我们令 \(pre_i\) 为最大的 \(j<i\) 使得 \(a_j=a_i\),若不存在则为 \(0\)。
这样转化成三维数点问题,即求满足下列条件的 \(i\) 的个数:
- \(i\in[l,r]\)
- \(a_i\in[a,b]\)
- \(pre_i\in[0,l-1]\)
用这个 \(pre\) 来解决区间数颜色问题是一个很常用的技巧,后面我们还会遇到~
第一维离线干掉,剩下两维树套树。
考虑到 \(pre_i\) 会取到 \(0\),为了方便实现,我们用树状数组维护第二维,线段树维护第三维。
由于第二问离线了,所以第一问跟着变成一维数点,开一个树状数组即可解决。
时间复杂度 \(O(n\log n\log V)\)。
节点总数 \(n\log n\log V\)。
点击查看代码 R224341732
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10,M=1e5+10,V=1e5;
int n,m,a[N],idx,pre[N],pos[V+10],root[V],ans[M][2],CNT;
struct Query{int id,v,p,oa,ob,ib;}q[M<<1];
inline int lb(int x){return x&-x;}
struct SEG{
int idx=0,lc[300*M],rc[300*M],sum[300*M];
void chp(int& x,int a,int v,int l,int r){
if(!x) x=++idx;
sum[x]+=v;
if(l==r) return;
int mid=(l+r)>>1;
if(a<=mid) chp(lc[x],a,v,l,mid);
else chp(rc[x],a,v,mid+1,r);
}
int query(int x,int a,int b,int l,int r){
if(a<=l&&r<=b) return sum[x];
int mid=(l+r)>>1,ans=0;
if(a<=mid) ans+=query(lc[x],a,b,l,mid);
if(b>mid) ans+=query(rc[x],a,b,mid+1,r);
return ans;
}
}seg;
struct firBIT{//二维数点用
int sum[V+10];
void chp(int x,int v){for(;x<=V;x+=lb(x)) sum[x]+=v;}
int query(int x){int ans=0;for(;x;x-=lb(x)) ans+=sum[x];return ans;}
int query(int x,int y){return query(y)-query(x-1);}
}fbit;
struct BIT{//三维数点用
void chp(int x,int ia,int iv){
for(;x<=V;x+=lb(x)) seg.chp(root[x],ia,iv,0,n);
}
int query(int x,int ia,int ib){
int ans=0;
for(;x;x-=lb(x)) ans+=seg.query(root[x],ia,ib,0,n);
return ans;
}
int query(int x,int y,int ia,int ib){
return query(y,ia,ib)-query(x-1,ia,ib);
}
}bit;
void solve(){
int t=0;
for(int i=1;i<=idx;i++){
while(t+1<=q[i].p) ++t,bit.chp(a[t],pre[t],1),fbit.chp(a[t],1),CNT++;
ans[q[i].id][0]+=q[i].v*fbit.query(q[i].oa,q[i].ob);
ans[q[i].id][1]+=q[i].v* bit.query(q[i].oa,q[i].ob,0,q[i].ib);
}
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i],pre[i]=pos[a[i]],pos[a[i]]=i;
for(int i=1,l,r,a,b;i<=m;i++){
cin>>l>>r>>a>>b;// ↓ 一个询问拆成俩
q[++idx]={i, -1, l-1, a, b, l-1};
q[++idx]={i, 1, r, a, b, l-1};
}
sort(q+1,q+1+idx,[](Query a,Query b){return a.p<b.p;});
solve();
for(int i=1;i<=m;i++) cout<<ans[i][0]<<" "<<ans[i][1]<<"\n";
return 0;
}
CF1093E Intersection of Permutations
很好玩的思维题。
注意到 \(a,b\) 都是 \(1,2,\dots,n\) 的排列,因此我们可以将 \(a_{i}\) 映射到 \(i\),\(b\) 也随之发生变化。显然这样子不会影响之后的查询。
这样求 \(|S_a\cap S_b|\),其实就是求 \(S_b\) 在 \([l_a,r_a]\) 值域上的元素个数,使用树套树即可解决。
另外,这道题不进行任何优化,节点总数达到 \((n+2m)\log^2 n\),空间会超限。因此我们可以使用节点回收来重复利用不需要的点(本题中,不需要的点就是被 sum 被减到 \(0\) 的点),节点总数降为 \(n\log^2 n\)。
虽然受空间限制仍然不能开到 \(n\log^2 n\),但是由于我们充分利用了之前的节点,并且实际情况下节点总数远小于理论上界,所以放心,不会有问题的 (^^;
代码中的 newnode()、del() 都是垃圾回收,原理见代码。
遇到节点数量不够用的题,节点回收是一个很好的习惯~
时间复杂度 \(O((n+m)\log^2 n)\)。
节点总数 \(n\log^2 n\)。
点击查看代码 #327886986
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int n,m,a[N],b[N],to[N],root[N];
inline int lowbit(int x){return x&-x;}
struct SEG{
stack<int> gar;
int idx;
struct node{
int lc,rc,sum;
void init(){*this={0,0,0};}
}tr[N*100];//虽然还是开不下Nlog^2 N,但是很难卡到空间上界
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define sum(x) (tr[x].sum)
void del(int &x){gar.push(x),x=0;}
void newnode(int &x){
if(!gar.empty()) x=gar.top(),gar.pop(),tr[x].init();
else x=++idx;
}
void chp(int &x,int a,int v,int l,int r){
if(!x) newnode(x);
sum(x)+=v;
if(l<r){
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
}
if(!sum(x)) del(x);
}
int query(int x,int a,int b,int l,int r){
if(a<=l&&r<=b) return sum(x);
int mid=(l+r)>>1,ans=0;
if(a<=mid) ans+=query(lc(x),a,b,l,mid);
if(b>mid) ans+=query(rc(x),a,b,mid+1,r);
return ans;
}
}tr;
struct BIT{
void chp(int x,int a,int v){
while(x<=n) tr.chp(root[x],a,v,1,n),x+=lowbit(x);
}
int query(int x,int a,int b){
int ans=0;
while(x) ans+=tr.query(root[x],a,b,1,n),x-=lowbit(x);
return ans;
}
}bit;
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i],to[a[i]]=i;
for(int i=1;i<=n;i++) cin>>b[i],b[i]=to[b[i]],bit.chp(i,b[i],1);
int op,la,ra,lb,rb,x,y;
while(m--){
cin>>op;
if(op==1){
cin>>la>>ra>>lb>>rb;
cout<<bit.query(rb,la,ra)-bit.query(lb-1,la,ra)<<"\n";
}else{
cin>>x>>y;
bit.chp(x,b[x],-1),bit.chp(y,b[y],-1);//先删
swap(b[x],b[y]);
bit.chp(x,b[x],1),bit.chp(y,b[y],1);//后加
}
}
return 0;
}
P2617 Dynamic Rankings
该题一改之前的区间求和,变成了区间第 \(k\) 小。
发现不能按上题的方法做了,因为区间第 \(k\) 小不能在从线段树每次的查询结果合并而来,而必须在作差后得到的线段树上完成。
当然也不能将所有节点都求出来,否则单次时间复杂度就带一个 \(O(n)\) 了。
只要现用现求,线段树遍历到哪个节点计算哪个节点就好,具体见代码。
int cnt[2],t[20][2];
struct SEG{
......
int query(int k,int l,int r){
if(l==r) return l;
int mid=(l+r)>>1,sum=0;
for(int i=1;i<=cnt[1];i++) sum+=sum(lc(t[i][1]));
for(int i=1;i<=cnt[0];i++) sum-=sum(lc(t[i][0]));
if(k<=sum){//左子树的sum>=k,说明第k名在左子树
for(int i=1;i<=cnt[1];i++) t[i][1]=lc(t[i][1]);
for(int i=1;i<=cnt[0];i++) t[i][0]=lc(t[i][0]);
return query(k,l,mid);
}else{//否则,第k名在右子树
for(int i=1;i<=cnt[1];i++) t[i][1]=rc(t[i][1]);
for(int i=1;i<=cnt[0];i++) t[i][0]=rc(t[i][0]);
return query(k-sum,mid+1,r);
}
}
}
struct BIT{
......
int query(int k,int l,int r){
cnt[0]=cnt[1]=0,l--;//t[][0]为要减的节点,t[][1]为要加的节点
while(r) t[++cnt[1]][1]=root[r],r-=lowbit(r);
while(l) t[++cnt[0]][0]=root[l],l-=lowbit(l);
return tr.query(k,1,tn);
}
}
注意离散化。
时间复杂度 \(O((n+m)\log^2 n)\)。
节点总数 \(n\log^2 n\)。
点击查看代码 R222231320
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,Q=1e5+10;
int n,q,a[N],tmp[N+Q],idx,tn,root[N];
int cnt[2],t[20][2];
unordered_map<int,int> ma;
inline int lowbit(int x){return x&-x;}
struct Ope{char c;int l,r,k;}op[Q];
struct SEG{
int idx;
struct node{int lc,rc,sum;}tr[N*18*18];
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define sum(x) (tr[x].sum)
void chp(int &x,int a,int v,int l,int r){
if(!x) x=++idx;
sum(x)+=v;
if(l==r) return;
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
}
int query(int k,int l,int r){
if(l==r) return l;
int mid=(l+r)>>1,sum=0;
for(int i=1;i<=cnt[1];i++) sum+=sum(lc(t[i][1]));
for(int i=1;i<=cnt[0];i++) sum-=sum(lc(t[i][0]));
if(k<=sum){
for(int i=1;i<=cnt[1];i++) t[i][1]=lc(t[i][1]);
for(int i=1;i<=cnt[0];i++) t[i][0]=lc(t[i][0]);
return query(k,l,mid);
}else{
for(int i=1;i<=cnt[1];i++) t[i][1]=rc(t[i][1]);
for(int i=1;i<=cnt[0];i++) t[i][0]=rc(t[i][0]);
return query(k-sum,mid+1,r);
}
}
}tr;
struct BIT{
void chp(int x,int a,int v){//第x棵线段树第pos位+v
while(x<=n) tr.chp(root[x],a,v,1,tn),x+=lowbit(x);
}
int query(int k,int l,int r){
cnt[0]=cnt[1]=0,l--;
while(r) t[++cnt[1]][1]=root[r],r-=lowbit(r);
while(l) t[++cnt[0]][0]=root[l],l-=lowbit(l);
return tr.query(k,1,tn);
}
}bit;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>q;
for(int i=1;i<=n;i++) cin>>a[i],tmp[++idx]=a[i];
for(int i=1;i<=q;i++){
cin>>op[i].c;
if(op[i].c=='Q') cin>>op[i].l>>op[i].r>>op[i].k;
else{
cin>>op[i].l>>op[i].k;
tmp[++idx]=op[i].k;
}
}
sort(tmp+1,tmp+1+idx);
tn=unique(tmp+1,tmp+idx+1)-tmp-1;
for(int i=1;i<=tn;i++) ma[tmp[i]]=i;
for(int i=1;i<=n;i++) a[i]=ma[a[i]],bit.chp(i,a[i],1);
for(int i=1;i<=q;i++){
if(op[i].c=='Q'){
cout<<tmp[bit.query(op[i].k,op[i].l,op[i].r)]<<"\n";
}else{
bit.chp(op[i].l,a[op[i].l],-1);
a[op[i].l]=ma[op[i].k];
bit.chp(op[i].l,a[op[i].l],1);
}
}
return 0;
}
P3380 【模板】树套树
查询第 \(k\) 名和 Dynamic Ranking 相同。
查询值 \(k\) 的排名,其实就是查权值线段树 \([1,k)\) 的和,再 \(+1\)。
查询 \(k\) 的前驱、后继,用前两个操作组合起来即可完成,具体见下面的代码,并不难理解。
点击查看代码 R222738377
#include<bits/stdc++.h>
using namespace std;
const int N=5e4+10,Q=5e4+10,inf=INT_MAX;
int n,tn,q,a[N],b[N+Q],idx,root[N];
int t[N][2],cnt[2];
unordered_map<int,int> ma;
struct Que{
int op,l,r,k;
}que[Q];
inline int lowbit(int x){return x&-x;}
struct SEG{
int idx;
struct node{int lc,rc,sum;}tr[(N+Q)*17*17];
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define sum(x) (tr[x].sum)
void chp(int &x,int a,int v,int l,int r){
if(!x) x=++idx;
sum(x)+=v;
if(l==r) return;
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
}
int query(int x,int a,int l,int r){
if(l==r) return sum(x);
int mid=(l+r)>>1;
if(a<=mid) return query(lc(x),a,l,mid);
else return query(rc(x),a,mid+1,r);
}
int kth(int k,int l,int r){//第k个1在哪个下标
if(l==r) return l;
int mid=(l+r)>>1,z=0;
for(int i=1;i<=cnt[1];i++) z+=sum(lc(t[i][1]));
for(int i=1;i<=cnt[0];i++) z-=sum(lc(t[i][0]));
if(k<=z){
for(int i=1;i<=cnt[1];i++) t[i][1]=lc(t[i][1]);
for(int i=1;i<=cnt[0];i++) t[i][0]=lc(t[i][0]);
return kth(k,l,mid);
}else{
for(int i=1;i<=cnt[1];i++) t[i][1]=rc(t[i][1]);
for(int i=1;i<=cnt[0];i++) t[i][0]=rc(t[i][0]);
return kth(k-z,mid+1,r);
}
}
int ran(int k,int l,int r){//下标在[1,k)的元素总和,实际排名还要+1
if(l==r) return 0;
int mid=(l+r)>>1;
if(k<=mid){
for(int i=1;i<=cnt[1];i++) t[i][1]=lc(t[i][1]);
for(int i=1;i<=cnt[0];i++) t[i][0]=lc(t[i][0]);
return ran(k,l,mid);
}else{
int z=0;
for(int i=1;i<=cnt[1];i++) z+=sum(lc(t[i][1])),t[i][1]=rc(t[i][1]);
for(int i=1;i<=cnt[0];i++) z-=sum(lc(t[i][0])),t[i][0]=rc(t[i][0]);
return z+ran(k,mid+1,r);
}
}
}tr;
struct BIT{
void chp(int x,int a,int v){
while(x<=n) tr.chp(root[x],a,v,1,tn),x+=lowbit(x);
}
void init(int l,int r){
cnt[0]=cnt[1]=0,l--;
while(l) t[++cnt[0]][0]=root[l],l-=lowbit(l);
while(r) t[++cnt[1]][1]=root[r],r-=lowbit(r);
}
int kth(int k,int l,int r){return init(l,r),b[tr.kth(k,1,tn)];}
int ran(int k,int l,int r){return init(l,r),tr.ran(k,1,tn)+1;}
int pre(int k,int l,int r){
int z=ran(k,l,r)-1;//k所在的名次-1,对应的值就是k的前驱了
return z?kth(z,l,r):-inf;
}
int nxt(int k,int l,int r){
if(k==tn) return inf;//ran的返回值始终在[1,n]之间,所以必须特判
int z=ran(k+1,l,r);
return z<=r-l+1?kth(z,l,r):inf;
}
}bit;
signed main(){
cin>>n>>q;
for(int i=1;i<=n;i++) cin>>a[i],b[++idx]=a[i];
for(int i=1,op,l,r,k;i<=q;i++){
l=r=k=0;
cin>>op;
if(op==3) cin>>l>>k;
else cin>>l>>r>>k;
if(op!=2) b[++idx]=k;
que[i]={op,l,r,k};
}
sort(b+1,b+1+idx);
tn=unique(b+1,b+1+idx)-b-1;
for(int i=1;i<=tn;i++) ma[b[i]]=i;
for(int i=1;i<=n;i++) a[i]=ma[a[i]],bit.chp(i,a[i],1);
for(int i=1;i<=q;i++){
auto [op,l,r,k]=que[i];
if(op==3){
bit.chp(l,a[l],-1);
a[l]=ma[k];
bit.chp(l,a[l],1);
}else if(op==1) cout<<bit.ran(ma[k],l,r)<<"\n";
else if(op==2) cout<<bit.kth(k,l,r)<<"\n";
else if(op==4) cout<<bit.pre(ma[k],l,r)<<"\n";
else cout<<bit.nxt(ma[k],l,r)<<"\n";
}
return 0;
}
P4175 [CTSC2008] 网络管理
此题大致有 \(2\) 种解法。
树链剖分
树上路径维护首先想到树剖。
用树剖将要操作的路径分成最多 \(\log n\) 段连续的区间,然后再用树套树来维护这些区间对应线段树的动态第 \(k\) 大。
有点毒瘤的说,好想但是不好写(我只能想到这个了 w),用来练手还是很不错的。
时间复杂度 \(O((n+m)\log^3 n)\)。
节点总数 \(n\log^3 n\)。
点击查看代码 R223183396
#include<bits/stdc++.h>
using namespace std;
const int N=8e4+10,Q=8e4+10;
int n,tn,q,idx,head[N],w[N],dc[N+Q];
int dep[N],fa[N],siz[N],son[N],top[N],dfn[N],tim;
int root[N],cnt[2],t[N][2];//t: nlog^2 n
unordered_map<int,int> ma;
inline int lowbit(int x){return x&-x;}
struct Que{int k,a,b;}qu[Q];
struct SEG{
stack<int> gar;
int idx;
struct node{
int lc,rc,sum;
void init(){*this={0,0,0};}
}tr[200*N];//tr: nlog^3 n
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define sum(x) (tr[x].sum)
void del(int &x){gar.push(x),x=0;}
void newnode(int &x){
if(!gar.empty()) x=gar.top(),gar.pop(),tr[x].init();
else x=++idx;
}
void chp(int &x,int a,int v,int l,int r){
if(!x) newnode(x);
sum(x)+=v;
if(l<r){
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
}
if(!sum(x)) del(x);
}
int kth(int k,int l,int r){
if(l==r) return l;
int mid=(l+r)>>1,z=0;
for(int i=1;i<=cnt[1];i++) z+=sum(rc(t[i][1]));
for(int i=1;i<=cnt[0];i++) z-=sum(rc(t[i][0]));
if(k<=z){
for(int i=1;i<=cnt[1];i++) t[i][1]=rc(t[i][1]);
for(int i=1;i<=cnt[0];i++) t[i][0]=rc(t[i][0]);
return kth(k,mid+1,r);
}else{
for(int i=1;i<=cnt[1];i++) t[i][1]=lc(t[i][1]);
for(int i=1;i<=cnt[0];i++) t[i][0]=lc(t[i][0]);
return kth(k-z,l,mid);
}
}
}tr;
struct BIT{
void chp(int x,int a,int v){
while(x<=n) tr.chp(root[x],a,v,1,tn),x+=lowbit(x);
}
}bit;
void clearT(){cnt[0]=cnt[1]=0;}
void addT(int l,int r){
l--;
while(r) t[++cnt[1]][1]=root[r],r-=lowbit(r);
while(l) t[++cnt[0]][0]=root[l],l-=lowbit(l);
}
struct edge{int nxt,to;}e[N<<1];
void add(int u,int v){e[++idx]={head[u],v},head[u]=idx;}
void dfs1(int u){
dep[u]=dep[fa[u]]+1,siz[u]=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa[u]) continue;
fa[v]=u,dfs1(v),siz[u]+=siz[v];
if(siz[v]>siz[son[u]]) son[u]=v;
}
}
void dfs2(int u,int t){
top[u]=t,dfn[u]=++tim;
if(son[u]) dfs2(son[u],t);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v!=son[u]&&v!=fa[u]) dfs2(v,v);
}
}
int qpath(int u,int v){//将u~v路径上的加减情况存储在t中,并返回u,v间的节点数量
int sum=0;
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]]) swap(u,v);
addT(dfn[top[u]],dfn[u]),sum+=dfn[u]-dfn[top[u]]+1;
u=fa[top[u]];
}
if(dep[u]<dep[v]) swap(u,v);
addT(dfn[v],dfn[u]);
return sum+dfn[u]-dfn[v]+1;
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>q;
for(int i=1;i<=n;i++) cin>>w[i],dc[++tn]=w[i];
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
add(u,v),add(v,u);
}
dfs1(1),dfs2(1,1);
for(int i=1;i<=q;i++){
cin>>qu[i].k>>qu[i].a>>qu[i].b;
if(!qu[i].k) dc[++tn]=qu[i].b;
}
sort(dc+1,dc+1+tn);
tn=unique(dc+1,dc+1+tn)-dc-1;
for(int i=1;i<=tn;i++) ma[dc[i]]=i;
for(int i=1;i<=n;i++) w[i]=ma[w[i]],bit.chp(dfn[i],w[i],1);
for(int i=1;i<=q;i++){
auto [k,a,b]=qu[i];
if(!k){
bit.chp(dfn[a],w[a],-1);
w[a]=ma[b];
bit.chp(dfn[a],w[a],1);
}else{
clearT();
if(qpath(a,b)<k) cout<<"invalid request!\n";
else cout<<dc[tr.kth(k,1,tn)]<<"\n";
}
}
return 0;
}
树上差分
参考了此题解 by jiqimao(实现真的非常优雅)。
要是这道题没有点修,我们其实根本不会瞥树剖一眼的,而是选择使用树上差分来维护一条路径的信息(这里的信息,其实就是一棵权值线段树啦),即:
\(u\) 到 \(v\) 的路径信息(拿点差分来举例),相当于:
- \(\ \ \ \ u\) 到根的路径信息
- \(+\ v\) 到根的路径信息
- \(-\ \text{LCA}(u,v)\) 到根的路径信息
- \(-\ fa_{\text{LCA}(u,v)}\) 到根的路径信息
现在有了点修操作,我们真的要臣服于树剖了吗?
实际上,我们如果已经记录了每个点到根节点的路径信息。那么对 \(u\) 进行点修,所影响的只有 \(u\) 子树中 点到根的路径信息。
我们将节点按 DFS 序编号,这样子树中节点的编号就是连续的。
因此外层的树状数组需要支持区间修改,单点查询。通过维护原序列的差分数组即可做到,可以参考此文 by RabbitHu。
内层正常跑动态开点的权值线段树就可以了。
时间复杂度 \(O((n+m)\log^2 n)\)。
节点总数 \(n\log^2 n\)。
点击查看代码 R223183057
#include<bits/stdc++.h>
using namespace std;
const int N=8e4+10,Q=8e4+10;
int n,tn,q,idx,head[N],w[N],dc[N+Q],root[N];
int dep[N],fa[N][17],dfn[N],tim,rr[N];
unordered_map<int,int> ma;
inline int lowbit(int x){return x&-x;}
struct Que{int k,a,b;}qu[Q];
struct edge{int nxt,to;}e[N<<1];
void add(int u,int v){e[++idx]={head[u],v},head[u]=idx;}
void dfs(int u,int ff){
fa[u][0]=ff,dep[u]=dep[ff]+1,dfn[u]=++tim;
for(int i=0;i<16;i++) fa[u][i+1]=fa[fa[u][i]][i];
for(int i=head[u];i;i=e[i].nxt) if(e[i].to!=ff) dfs(e[i].to,u);
rr[u]=tim;//子树u的时间戳:dfn[u]~rr[u]
}
int lca(int u,int v){
if(dep[u]<dep[v]) swap(u,v);
for(int i=16;~i;i--) if(dep[fa[u][i]]>=dep[v]) u=fa[u][i];
if(u==v) return u;
for(int i=16;~i;i--) if(fa[u][i]!=fa[v][i]) u=fa[u][i],v=fa[v][i];
return fa[u][0];
}
struct node{int lc,rc,sum;}tr[200*N];//nlog^2 n
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define sum(x) (tr[x].sum)
struct group{
int n,a[N];
int calc(){int ans=0;for(int i=1;i<=n;i++) ans+=sum(rc(a[i]));return ans;}
void L(){for(int i=1;i<=n;i++) a[i]=lc(a[i]);}
void R(){for(int i=1;i<=n;i++) a[i]=rc(a[i]);}
void init(int x){n=0;for(;x;x-=lowbit(x)) a[++n]=root[x];}
}A,B,C,D;
struct SEG{
int idx;
void chp(int& x,int a,int v,int l,int r){
if(!x) x=++idx;
sum(x)+=v;
if(l==r) return;
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
}
int kth(int k,int l,int r){
if(l==r) return l;
int mid=(l+r)>>1,z=A.calc()+B.calc()-C.calc()-D.calc();
if(k<=z) return A.R(),B.R(),C.R(),D.R(),kth(k,mid+1,r);
else return A.L(),B.L(),C.L(),D.L(),kth(k-z,l,mid);
}
}seg;
struct BIT{
void chp(int x,int a,int v){
while(x<=n) seg.chp(root[x],a,v,1,tn),x+=lowbit(x);
}
void chr(int x,int y,int a,int v){
chp(x,a,v),chp(y+1,a,-v);
}
}bit;
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>q;
for(int i=1;i<=n;i++) cin>>w[i],dc[++tn]=w[i];
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
add(u,v),add(v,u);
}
dfs(1,0);
for(int i=1;i<=q;i++){
cin>>qu[i].k>>qu[i].a>>qu[i].b;
if(!qu[i].k) dc[++tn]=qu[i].b;
}
sort(dc+1,dc+1+tn);
tn=unique(dc+1,dc+1+tn)-dc-1;
for(int i=1;i<=tn;i++) ma[dc[i]]=i;
for(int i=1;i<=n;i++) w[i]=ma[w[i]],bit.chr(dfn[i],rr[i],w[i],1);
for(int i=1;i<=q;i++){
auto [k,a,b]=qu[i];
if(!k){
bit.chr(dfn[a],rr[a],w[a],-1);
bit.chr(dfn[a],rr[a],w[a]=ma[b],1);
}else{
int z=lca(a,b);
if(dep[a]+dep[b]-2*dep[z]+1<k) cout<<"invalid request!\n";
else A.init(dfn[a]),B.init(dfn[b]),C.init(dfn[z]),D.init(dfn[fa[z][0]]),
cout<<dc[seg.kth(k,1,tn)]<<"\n";
}
}
return 0;
}
P3332 [ZJOI2013] K 大数查询
根据题意,我们知道:
- 维护下标的结构需要支持:区间修改、区间查询。
- 维护值域的结构需要支持:单点修改、区间 k-th。
这和之前是不一样的。因为此前的题都是对同一个下标进行操作,这样就算需要区间修改,也是在内层结构上进行的;而这道题则是一次性对多个下标进行操作。
由此,写这道题我们大致有 \(2\) 个方向。
内外反套
实际上反转一下数对的顺序,不影响我们解决二维偏序问题。
放在此题,就是用外层的树状数组来维护值域,内层线段树来维护下标。
不过这就需要我们的树状数组支持区间 k-th,这就需要树状数组上倍增。
查询第 \(k\) 小的代码如下。
int kth(int k,int a,int b){//即寻找最小的x使得a[1~x]>=k
int x=0,sum=0;
for(int i=1<<__lg(n);i;i>>=1){//1<<__lg(n)即n的highbit
if(x+i>n) continue;
int f=a[i]+sum;
if(f<k) x+=i,sum=f;
}
return x+1;
}
为了减少常数,内层线段树的区间操作建议使用标记永久化。
#1 Code R223706490
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e4+10,M=5e4+10;
int n,m,root[M],b[M],tn;
unordered_map<int,int> ma;
struct Que{int op,l,r,c;}q[M];
inline int lowbit(int x){return x&-x;}
struct SEG{
int idx;
struct node{int lc,rc,sum,tag;}tr[300*M];//MlogMlogN
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define sum(x) (tr[x].sum)
#define tag(x) (tr[x].tag)
int clone(int x){return tr[++idx]=tr[x],idx;}
void chr(int &x,int a,int b,int v,int l,int r){
x=clone(x);
sum(x)+=(b-a+1)*v;
if(a==l&&b==r) return tag(x)+=v,void();
int mid=(l+r)>>1;
if(b<=mid) chr(lc(x),a,b,v,l,mid);
else if(a>mid) chr(rc(x),a,b,v,mid+1,r);
else chr(lc(x),a,mid,v,l,mid),chr(rc(x),mid+1,b,v,mid+1,r);
}
int query(int x,int a,int b,int l,int r){
if(a==l&&b==r) return sum(x);
int mid=(l+r)>>1,sum=(b-a+1)*tag(x);
if(b<=mid) return sum+query(lc(x),a,b,l,mid);
else if(a>mid) return sum+query(rc(x),a,b,mid+1,r);
else return sum+query(lc(x),a,mid,l,mid)+query(rc(x),mid+1,b,mid+1,r);
}
}seg;
struct BIT{
void chp(int x,int ia,int ib,int iv){
for(;x<=tn;x+=lowbit(x)) seg.chr(root[x],ia,ib,iv,1,n);
}
int kth(int k,int a,int b){//由于已经从大到小排序,所以实际上是求第k小
int x=0,sum=0;//即寻找最小的x使得a[1~x]>=k
for(int i=1<<__lg(tn);i;i>>=1){
if(x+i>tn) continue;
int f=seg.query(root[x+i],a,b,1,n)+sum;
if(f<k) x+=i,sum=f;
}
return x+1;
}
}bit;
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>q[i].op>>q[i].l>>q[i].r>>q[i].c;
if(q[i].op==1) b[++tn]=q[i].c;
}
sort(b+1,b+1+tn),tn=unique(b+1,b+1+tn)-b-1;
reverse(b+1,b+1+tn);//从大到小
for(int i=1;i<=tn;i++) ma[b[i]]=i;
for(int i=1;i<=m;i++){
if(q[i].op==1) bit.chp(ma[q[i].c],q[i].l,q[i].r,1);
else cout<<b[bit.kth(q[i].c,q[i].l,q[i].r)]<<"\n";
}
return 0;
}
外层写线段树也是可以的,毕竟线段树上二分求 k-th 还是很常见的。
#2 Code R223707237
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e4+10,M=5e4+10;
int n,m,root[M<<1],b[M],tn;//(M<<1)是因为线段树用2倍节点
unordered_map<int,int> ma;
struct Que{int op,l,r,c;}q[M];
struct innerSEG{
int idx;
struct node{int lc,rc,sum,tag;}tr[500*M];//2*MlogMlogN,*2是因为线段树用2倍节点
inline int& lc(int x){return tr[x].lc;}
inline int& rc(int x){return tr[x].rc;}
inline int& sum(int x){return tr[x].sum;}
inline int& tag(int x){return tr[x].tag;}
int clone(int x){return tr[++idx]=tr[x],idx;}
void chr(int &x,int a,int b,int v,int l,int r){
x=clone(x);
sum(x)+=(b-a+1)*v;
if(a==l&&b==r) return tag(x)+=v,void();
int mid=(l+r)>>1;
if(b<=mid) chr(lc(x),a,b,v,l,mid);
else if(a>mid) chr(rc(x),a,b,v,mid+1,r);
else chr(lc(x),a,mid,v,l,mid),chr(rc(x),mid+1,b,v,mid+1,r);
}
int query(int x,int a,int b,int l,int r){
if(a==l&&b==r) return sum(x);
int mid=(l+r)>>1,sum=(b-a+1)*tag(x);
if(b<=mid) return sum+query(lc(x),a,b,l,mid);
else if(a>mid) return sum+query(rc(x),a,b,mid+1,r);
else return sum+query(lc(x),a,mid,l,mid)+query(rc(x),mid+1,b,mid+1,r);
}
}in;
struct outerSEG{
inline int lc(int x){return x<<1;}
inline int rc(int x){return x<<1|1;}
void chp(int x,int a,int ia,int ib,int l,int r){
in.chr(root[x],ia,ib,1,1,n);
if(l==r) return;
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,ia,ib,l,mid);
else chp(rc(x),a,ia,ib,mid+1,r);
}
int kth(int x,int k,int ia,int ib,int l,int r){
if(l==r) return l;
int mid=(l+r)>>1,z=in.query(root[rc(x)],ia,ib,1,n);
if(k<=z) return kth(rc(x),k,ia,ib,mid+1,r);
else return kth(lc(x),k-z,ia,ib,l,mid);
}
}out;
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>q[i].op>>q[i].l>>q[i].r>>q[i].c;
if(q[i].op==1) b[++tn]=q[i].c;
}
sort(b+1,b+1+tn),tn=unique(b+1,b+1+tn)-b-1;
for(int i=1;i<=tn;i++) ma[b[i]]=i;
for(int i=1;i<=m;i++){
if(q[i].op==1) out.chp(1,ma[q[i].c],q[i].l,q[i].r,1,tn);
else cout<<b[out.kth(1,q[i].c,q[i].l,q[i].r,1,tn)]<<"\n";
}
return 0;
}
使用支持区修、区查的外层结构
如果我们还是选择使用外层维护下标,也是可以做的。
虽然说一般的树状数组仅支持“点修 + 区查”,但我仍然可以利用刚才维护差分序列的思路,让我们的树状数组支持“区修 + 区查”。具体来说(仍然参考此文 by RabbitHu):
令 \(d\) 为 \(a\) 的差分数组,则有:
\[\begin{aligned} \sum\limits_{i=1}^x a[i] &=\sum\limits_{i=1}^x \sum\limits_{j=1}^ i d[j]\\ &=\sum\limits_{i=1}^x (x-i+1)\times d[i]\\ &=(x+1)\sum\limits_{i=1}^x d[i]-\sum\limits_{i=1}^x i\times d[i] \end{aligned}\]因此在上文维护 \(d[i]\) 的基础上,额外开一个数组维护 \(d[i]\times i\) 即可。即:
void add(ll p, ll x){ for(int i = p; i \le n; i += i & -i) sum1[i] += x, sum2[i] += x \times p; } void range_add(ll l, ll r, ll x){ add(l, x), add(r + 1, -x); } ll ask(ll p){ ll res = 0; for(int i = p; i; i -= i & -i) res += (p + 1) \times sum1[i] - sum2[i]; return res; } ll range_ask(ll l, ll r){ return ask(r) - ask(l - 1); }\[\]
于是我们就可以愉快地搓树状数组套权值线段树了。
#3 Code R223707459
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e4+10,M=5e4+10;
int n,m,root[N<<1],b[M],tn;//(N<<1)是因为树状数组要维护两个sum[],见题解
unordered_map<int,int> ma;
inline int lowbit(int x){return x&-x;}
struct Que{int op,l,r,c;}q[M];
struct node{int lc,rc,sum;}tr[300*N];//MlogNlogM
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define sum(x) (tr[x].sum)
struct group{
int n,a[80],v[80];//4logN
int calc(){int ans=0;for(int i=1;i<=n;i++) ans+=v[i]*sum(rc(a[i]));return ans;}
void L(){for(int i=1;i<=n;i++) a[i]=lc(a[i]);}
void R(){for(int i=1;i<=n;i++) a[i]=rc(a[i]);}
}A;
struct SEG{
int idx;
void chp(int &x,int a,int v,int l,int r){
if(!x) x=++idx;
sum(x)+=v;
if(l==r) return;
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
}
int kth(int k,int l,int r){
if(l==r) return l;
int mid=(l+r)>>1,z=A.calc();
if(k<=z) return A.R(),kth(k,mid+1,r);
else return A.L(),kth(k-z,l,mid);
}
}seg;
struct BIT{
void chp(int x,int ia,int iv){
for(int i=x;i<=n;i+=lowbit(i)) seg.chp(root[i],ia,iv,1,tn),seg.chp(root[i+N],ia,iv*x,1,tn);
}
void chr(int x,int y,int ia,int iv){
chp(x,ia,iv),chp(y+1,ia,-iv);
}
int query(int x,int y,int ik){
A.n=0,x--;
for(int i=y;i;i-=lowbit(i)) A.v[++A.n]=y+1,A.a[A.n]=root[i],A.v[++A.n]=-1,A.a[A.n]=root[i+N];
for(int i=x;i;i-=lowbit(i)) A.v[++A.n]=-(x+1),A.a[A.n]=root[i],A.v[++A.n]=1,A.a[A.n]=root[i+N];
return seg.kth(ik,1,tn);
}
}bit;
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>q[i].op>>q[i].l>>q[i].r>>q[i].c;
if(q[i].op==1) b[++tn]=q[i].c;
}
sort(b+1,b+1+tn),tn=unique(b+1,b+1+tn)-b-1;
for(int i=1;i<=tn;i++) ma[b[i]]=i;
for(int i=1;i<=m;i++){
if(q[i].op==1) bit.chr(q[i].l,q[i].r,ma[q[i].c],1);
else cout<<b[bit.query(q[i].l,q[i].r,q[i].c)]<<"\n";
}
return 0;
}
本来还考虑外层换成线段树试试,不过区修有点难以应对,因为操作的不是数而是一棵棵内层线段树,所以标记不能叠加要一个个下放,就算延迟下放也不能降低时间复杂度;标记永久化也无法使用。遂放弃之。
时间复杂度 \(O(m\log m\log n)\)。
节点总数 \(m\log m\log n\)。
下图是三种代码实现的比较(代码大小不含注释):
最后一种很显著地快啊……可能是因为大部分操作都丢给树状数组,线段树不需要维护区间操作的原因。
由此也可见,树状数组比线段树还是快了不少的,而且区修 + 区查 + 区 k-th 这些操作树状数组都能做到。除了不能动态开点,所以只能套在外面(否则空间会炸),在维护基础操作方面,绝对碾压线段树好伐!
P3242 [HNOI2015] 接水果
根据题意,水果 \((x,y)\) 能被盘子 \((u,v)\) 接住 \(\iff\) 路径 \((x,y)\) 包含路径 \((u,v)\)。
因此考虑 \((x,y)\) 什么满足什么情况时包含 \((u,v)\)。
定义 \(L_i\) 为 \(i\) 的 DFS 序,\(R_i\) 为子树 \(i\) 中最大的 DFS 序。
不妨令 \(L_u<L_v\),\(L_x<L_y\)。
则进行分类讨论:
-
\(\text{LCA}(u,v)\neq u\)
显然 \(x\) 在子树 \(u\) 中,\(y\) 在子树 \(v\) 中,即 \(L_x\in[L_u,R_u],L_y\in[L_v,R_v]\)。
-
\(\text{LCA}(u,v)=u\)
设 \(z\) 为 \(u\rightarrow v\) 路径上第二个节点(如下图),则 \(x,y\) 必有一个在子树 \(v\) 中,另一个在子树 \(z\) 外。
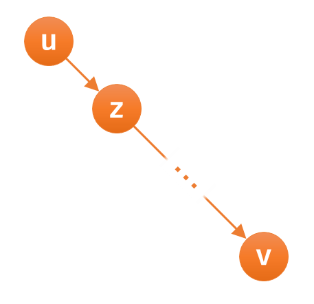
即 \(L_x\in[1,L_z),L_y\in[L_v,R_v]\),或 \(L_x\in [L_v,R_v],L_y\in (R_z,n]\)。
我们发现,若将路径 \((x,y)\) 映射为二维平面上的点 \((L_x,L_y)\),路径 \((u,v)\) 给出的限制看作二维平面上的 \(1\) 或 \(2\) 个矩形的话,\((L_x,L_y)\) 被矩形覆盖 \(\iff\) 路径 \((x,y)\) 包含路径 \((u,v)\)。
而且由于第二种情况的 \(2\) 个矩形是不交的,所以不会重复统计贡献。原问题转化为:查询覆盖 \((L_x,L_y)\) 的所有矩形中,权值的第 \(k\) 大是多少。
我们可以用类似扫描线的算法,先为每个 y 坐标建一棵权值线段树,再从左往右扫描竖向的线段 \((l,r)\) 和待查询的点:
- 遇到左端点则将编号 \([l,r]\) 线段树的 \(w\) 处 \(+1\);
- 遇到右端点则将编号 \([l,r]\) 线段树的 \(w\) 处 \(-1\);
- 遇到待查询的点 \((L_x,L_y)\) 时,直接统计编号 \(L_y\) 的线段树的第 \(k\) 小即可。
操作和上道题类似,不过区间查变成单点查了。我写的是 #3 的实现~
点击查看代码 R224022912
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=4e4+10,P=4e4+10,Q=4e4+10;
int n,p,q,tn,eidx,sidx,head[N],b[P],root[N];
int tim,fa[N][17],dep[N],dfn[N],rig[N],ans[Q];
unordered_map<int,int> ma;
struct edge{int nxt,to;}e[N<<1];
struct Border{int x,l,r,p,v;}bor[P<<2];//描述一条纵向线段
struct Query{int u,v,k,id;}qu[Q];
void add(int u,int v){e[++eidx]={head[u],v},head[u]=eidx;}
inline int lb(int x){return x&-x;}
int lc[300*N],rc[300*N],sum[300*N];
struct group{
int n,a[20];
void append(int x){a[++n]=x;}
int calc(){int ans=0;for(int i=1;i<=n;i++) ans+=sum[lc[a[i]]];return ans;}
void L(){for(int i=1;i<=n;i++) a[i]=lc[a[i]];}
void R(){for(int i=1;i<=n;i++) a[i]=rc[a[i]];}
}A;
struct SEG{
int idx;
void chp(int &x,int a,int v,int l,int r){
if(!x) x=++idx;
sum[x]+=v;
if(l==r) return;
int mid=(l+r)>>1;
if(a<=mid) chp(lc[x],a,v,l,mid);
else chp(rc[x],a,v,mid+1,r);
}
int kth(int k,int l,int r){
if(l==r) return l;
int mid=(l+r)>>1,z=A.calc();
if(k<=z) return A.L(),kth(k,l,mid);
else return A.R(),kth(k-z,mid+1,r);
}
}seg;
struct BIT{//区修 点查
void chp(int x,int ia,int iv){
while(x<=n) seg.chp(root[x],ia,iv,1,tn),x+=lb(x);
}
void chr(int x,int y,int ia,int iv){
chp(x,ia,iv),chp(y+1,ia,-iv);
}
int query(int x,int ik){
A.n=0;
while(x) A.append(root[x]),x-=lb(x);
return seg.kth(ik,1,tn);
}
}bit;
void dfs(int u){
dfn[u]=++tim,dep[u]=dep[fa[u][0]]+1;
for(int i=0;i<16;i++) fa[u][i+1]=fa[fa[u][i]][i];
for(int i=head[u];i;i=e[i].nxt){
if(e[i].to==fa[u][0]) continue;
fa[e[i].to][0]=u,dfs(e[i].to);
}
rig[u]=tim;
}
int LCA(int u,int v,int& z){
if(dep[u]<dep[v]) swap(u,v);
for(int i=16;~i;i--) if(dep[fa[u][i]]>dep[v]) u=fa[u][i];
if(dep[u]>dep[v]) z=u,u=fa[u][0];
if(u==v) return u;
for(int i=16;~i;i--) if(fa[u][i]!=fa[v][i]) u=fa[u][i],v=fa[v][i];
return fa[u][0];
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>p>>q;
for(int i=1,u,v;i<n;i++) cin>>u>>v,add(u,v),add(v,u);
dfs(1);
for(int i=1,u,v,w,z;i<=p;i++){
cin>>u>>v>>w,b[++tn]=w;
if(dfn[u]>dfn[v]) swap(u,v);
if(LCA(u,v,z)!=u){
bor[++sidx]={dfn[u],dfn[v],rig[v],w,1};
bor[++sidx]={rig[u]+1,dfn[v],rig[v],w,-1};
}else{
bor[++sidx]={1,dfn[v],rig[v],w,1};
bor[++sidx]={dfn[z],dfn[v],rig[v],w,-1};
bor[++sidx]={dfn[v],rig[z]+1,n,w,1};
bor[++sidx]={rig[v]+1,rig[z]+1,n,w,-1};
}
}
sort(bor+1,bor+1+sidx,[](Border a,Border b){return a.x<b.x;});
sort(b+1,b+1+tn),tn=unique(b+1,b+1+tn)-b-1;
for(int i=1;i<=tn;i++) ma[b[i]]=i;
bor[sidx+1].x=LLONG_MAX;
for(int i=1;i<=q;i++){
cin>>qu[i].u>>qu[i].v>>qu[i].k,qu[i].id=i;
if(dfn[qu[i].u]>dfn[qu[i].v]) swap(qu[i].u,qu[i].v);
}
sort(qu+1,qu+1+q,[](Query a,Query b){return dfn[a.u]<dfn[b.u];});
for(int i=1,p=0;i<=q;i++){
auto [u,v,k,num]=qu[i];
while(bor[p+1].x<=dfn[u]) ++p,bit.chr(bor[p].l,bor[p].r,ma[bor[p].p],bor[p].v);
ans[num]=b[bit.query(dfn[v],k)];
}
for(int i=1;i<=q;i++) cout<<ans[i]<<"\n";
return 0;
}
P4093 [HEOI2016 / TJOI2016] 序列
树套树优化 dp 的例题(不过这方面其实 CDQ 分治用的比较多)。
令 \(\max x_{i}\) 为 \(a_{i}\) 能变到的最大值,\(\min n_{i}\) 为 \(a_{i}\) 能变到的最小值,\(f_{i}\) 为以 \(a_{i}\) 为结尾的最长不降子序列的长度。则有转移:
其中 \(j\) 需要满足:
- \(j<i\)
- \(\max x_{j}\le a_{i}\)
- \(a_{j}\le \min n_{i}\)
套路三维数点。通过按 \(1,2,\dots,n\) 的顺序添加节点干点第一维,然后用外层树状数组维护第二条的 \(\max x\),内层线段树维护第三条的 \(a\)。
查询结果即为所有满足该条件的 \(j\) 中,\(f_{j}\) 的最大值。
尽管 \(\max\) 不可减,但是每次的查询在树状数组上都是一个前缀,因此不需要做减法。
顺带一提,树状数组维护 \(\max\) 有一定的局限性,比如只能支持前缀 / 后缀查询,且如果要支持点修,每次修改必须大于原位置的值。
时间复杂度 \(O(n\log^2 n)\)。
节点总数 \(n\log^2 n\)。
点击查看代码 R223759174
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,M=1e5+10;
int n,m,a[N],minn[N],maxx[N],root[N],f[N];
inline int lb(int x){return x&-x;}
struct SEG{
int idx;
int lc[300*N],rc[300*N],maxx[300*N];//Nlog^2 N
void sep(int& x,int a,int v,int l,int r){
if(!x) x=++idx;
if(l==r) return maxx[x]=max(maxx[x],v),void();
int mid=(l+r)>>1;
if(a<=mid) sep(lc[x],a,v,l,mid);
else sep(rc[x],a,v,mid+1,r);
maxx[x]=max(maxx[lc[x]],maxx[rc[x]]);
}
int query(int x,int a,int b,int l,int r){
if(a<=l&&r<=b) return maxx[x];
int mid=(l+r)>>1,ans=0;
if(a<=mid) ans=max(ans,query(lc[x],a,b,l,mid));
if(b>mid) ans=max(ans,query(rc[x],a,b,mid+1,r));
return ans;
}
}seg;
struct BIT{
void sep(int x,int ia,int iv){
for(;x<=n;x+=lb(x)) seg.sep(root[x],ia,iv,1,n);
}
int query(int x,int ia,int ib){
int ans=0;
for(;x;x-=lb(x)) ans=max(ans,seg.query(root[x],ia,ib,1,n));
return ans;
}
}bit;
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i],maxx[i]=minn[i]=a[i];
while(m--){
int x,y;
cin>>x>>y;
maxx[x]=max(maxx[x],y);
minn[x]=min(minn[x],y);
}
for(int i=1;i<=n;i++){
f[i]=1+bit.query(a[i],1,minn[i]);
bit.sep(maxx[i],a[i],f[i]);
}
cout<<*max_element(f+1,f+1+n)<<"\n";
return 0;
}
P3364 Cool loves touli
与上题类似。
先按等级从小到大排序,令每个英雄的后三个属性分别是 \(a_{i},b_{i},c_{i}\),\(f_{i}\) 表示以 \(i\) 结束的选择方案最多包含多少个英雄。则有转移:
其中 \(j\) 需要满足:
- \(j<i\)
- \(c_{j}\le a_{i}\)
- \(b_{j}\le c_{i}\)
和上题一样做就行,如果得 \(60\) 分你就做对了,因为空间限制不放我们的树套树过 (^^;
点击查看代码 R223752866
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
struct Hero{int l,a,b,c;}s[N];
int n,b[3*N],tn,f[N],root[N];
unordered_map<int,int> ma;
inline int lb(int x){return x&-x;}
struct SEG{
int idx;
int lc[400*N],rc[400*N],maxx[400*N];//Nlog^2(3N)
void sep(int& x,int a,int v,int l,int r){
if(!x) x=++idx;
if(l==r) return maxx[x]=max(maxx[x],v),void();
int mid=(l+r)>>1;
if(a<=mid) sep(lc[x],a,v,l,mid);
else sep(rc[x],a,v,mid+1,r);
maxx[x]=max(maxx[lc[x]],maxx[rc[x]]);
}
int query(int x,int a,int b,int l,int r){
if(a<=l&&r<=b) return maxx[x];
int mid=(l+r)>>1,ans=0;
if(a<=mid) ans=max(ans,query(lc[x],a,b,l,mid));
if(b>mid) ans=max(ans,query(rc[x],a,b,mid+1,r));
return ans;
}
}seg;
struct BIT{
void sep(int x,int ia,int iv){
for(;x<=tn;x+=lb(x)) seg.sep(root[x],ia,iv,1,tn);
}
int query(int x,int ia,int ib){
int ans=0;
for(;x;x-=lb(x)) ans=max(ans,seg.query(root[x],ia,ib,1,tn));
return ans;
}
}bit;
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>s[i].l>>s[i].a>>s[i].b>>s[i].c;
b[++tn]=s[i].a,b[++tn]=s[i].b,b[++tn]=s[i].c;
}
sort(b+1,b+1+tn),tn=unique(b+1,b+1+tn)-b-1;
for(int i=1;i<=tn;i++) ma[b[i]]=i;
sort(s+1,s+1+n,[](Hero a,Hero b){return a.l<b.l;});
for(int i=1;i<=n;i++){
auto [ignore,a,b,c]=s[i];
a=ma[a],b=ma[b],c=ma[c];
f[i]=1+bit.query(a,1,c);
bit.sep(c,b,f[i]);
}
cout<<*max_element(f+1,f+1+n)<<"\n";
return 0;
}
P1903 [国家集训队] 数颜色 / 维护队列
本质上是 P1972 [SDOI2009] HH 的项链加了个点修。
套路区间数颜色,仍然记 \(pre_{i}\) 为 \(a_{i}\) 上一次出现的位置,若没有则为 \(0\)。查询时仅需查询满足下面两个条件的 \(i\) 的个数:
- \(i\in [l,r]\)
- \(pre_{i}\in [0,l-1]\)
点修直接套用 CF848C Goodbye Souvenir,每次最多修改三个点即可解决。
点击查看代码 R225074108
#include<bits/stdc++.h>
using namespace std;
const int N=133333+10,M=133333+10;
int n,m,tn,a[N],b[N+M],root[N];
unordered_map<int,int> ma;
set<int> p[N+M];
struct Query{char op;int x,y;}q[M];
struct SEG{
int idx,lc[200*N],rc[200*N],sum[200*N];
void chp(int& x,int a,int v,int l,int r){
if(!x) x=++idx;
sum[x]+=v;
if(l==r) return;
int mid=(l+r)>>1;
if(a<=mid) chp(lc[x],a,v,l,mid);
else chp(rc[x],a,v,mid+1,r);
}
int query(int x,int a,int b,int l,int r){
if(a<=l&&r<=b) return sum[x];
int mid=(l+r)>>1,ans=0;
if(a<=mid) ans+=query(lc[x],a,b,l,mid);
if(b>mid) ans+=query(rc[x],a,b,mid+1,r);
return ans;
}
}seg;
inline int lb(int x){return x&-x;}
struct BIT{
void chp(int x,int ia,int iv){
for(;x<=n;x+=lb(x)) seg.chp(root[x],ia,iv,0,n);
}
int query(int x,int ia,int ib){
int ans=0;
for(;x;x-=lb(x)) ans+=seg.query(root[x],ia,ib,0,n);
return ans;
}
int query(int x,int y,int ia,int ib){
return query(y,ia,ib)-query(x-1,ia,ib);
}
}bit;
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i],b[++tn]=a[i];
for(int i=1;i<=m;i++){
cin>>q[i].op>>q[i].x>>q[i].y;
if(q[i].op=='R') b[++tn]=q[i].y;
}
sort(b+1,b+1+tn),tn=unique(b+1,b+1+tn)-b-1;
for(int i=1;i<=tn;i++) ma[b[i]]=i;
for(int i=1,pre;i<=n;i++){
a[i]=ma[a[i]];
pre=p[a[i]].empty()?0:(*p[a[i]].rbegin());
bit.chp(i,pre,1);
p[a[i]].insert(i);
}
set<int>::iterator it;
for(int i=1,pre,nxt;i<=m;i++){
auto [op,x,y]=q[i];
if(op=='Q'){
cout<<bit.query(x,y,0,x-1)<<"\n";
}else{
y=ma[y];
p[a[x]].erase(x);
it=p[y].lower_bound(x+1),pre=0;//1.与新颜色相同的后一位
if(it!=p[y].begin()) pre=*(--it);
it=p[y].upper_bound(x);
if(it!=p[y].end()){
nxt=*it;
bit.chp(nxt,x,1);
bit.chp(nxt,pre,-1);
}
it=p[a[x]].lower_bound(x+1),pre=0;//2.与旧颜色相同的后一位
if(it!=p[a[x]].begin()) pre=*(--it);
it=p[a[x]].upper_bound(x);
if(it!=p[a[x]].end()){
nxt=*it;
bit.chp(nxt,x,-1);
bit.chp(nxt,pre,1);
}
bit.chp(x,pre,-1);//3.被修改的位置
a[x]=y,pre=0;
it=p[y].lower_bound(x+1);
if(it!=p[y].begin()) pre=*(--it);
p[y].insert(x);
bit.chp(x,pre,1);
}
}
return 0;
}
P4690 [Ynoi Easy Round 2016] 镜中的昆虫 ~ LOJ #6201.
Ynoi 一血……?不过要提前说下,洛谷在卡根号空间的同时也把 \(\log^2\) 空间卡掉了,所以树状数组套权值线段树应该是过不掉的。不过你可以在空间限制更宽松的 LOJ 提交,亲测可过~
神题。
本质上是将上题的点修变成区修。
我们不妨沿用上题的思路,就 \(pre\) 数组进行分析。查询和上题相同,我们主要分析区间赋值。
先给结论:对长度为 \(n\) 的序列进行 \(m\) 次区间赋值操作后,\(pre\) 数组的变化次数为 \(O(n+m)\) 级别。
简单证明一下:
如果我们将同色连续段称作一个块,那么不难发现,除了块的开头,其他位置的 \(pre\) 值全部都是其下标 \(-1\)。
而每次区修一定可以拆成若干个块拼起来(若不能恰好取到左右端点,则将左右端点所在的块分裂),修改完成后这些小的块会被消掉,变成一个大的块。则此过程中发生变化的 \(pre\) 值仅有:
- 这些块开头的 \(pre\) 值。
- 所操作的区间右侧,与各个块原颜色相同的第一个位置。
两者同阶,故每次操作 \(pre\) 的变化次数是 \(O(\) 删去的块的个数 \()\),而每次我们最多添加 \(3\) 个块(左右端点所在的块分裂算 \(2\) 个,最后的大块算 \(1\) 个),所以删去的块的个数是 \(O(n+m)\) 数量级的,这样就得证了。
于是我们就可以用 set 来维护每个块,修改 \(pre\) 的时候在树套树上同步更新即可。
点击查看代码 2372872
#include<bits/stdc++.h>
#include<ext/pb_ds/hash_policy.hpp>
#include<ext/pb_ds/assoc_container.hpp>
using namespace std;
using namespace __gnu_pbds;
const int N=1e5+1,M=1e5+1;
int n,m,tn,a[N],b[N+M],pre[N],lst[N+M],st[N+M],top,root[N];
bitset<N+M> in;
struct Que{int l,r,x;}q[M];
gp_hash_table<int,int> ma;
set<int> ra,p[N+M];//ra记录所有块的左端点,p[i]记录颜色为i的所有块的左端点
struct SEG{
int idx,lc[200*N],rc[200*N],sum[200*N];
void chp(int& x,int a,int v,int l,int r){
if(!x) x=++idx;
sum[x]+=v;
if(l==r) return;
int mid=(l+r)>>1;
if(a<=mid) chp(lc[x],a,v,l,mid);
else chp(rc[x],a,v,mid+1,r);
}
int query(int x,int a,int b,int l,int r){
if(a<=l&&r<=b) return sum[x];
int mid=(l+r)>>1,ans=0;
if(a<=mid) ans+=query(lc[x],a,b,l,mid);
if(b>mid) ans+=query(rc[x],a,b,mid+1,r);
return ans;
}
}seg;
inline int lb(int x){return x&-x;}
struct BIT{
void chp(int x,int ia,int iv){
for(;x<=n;x+=lb(x)) seg.chp(root[x],ia,iv,0,n);
}
int query(int x,int ia,int ib){
int ans=0;
for(;x;x-=lb(x)) ans+=seg.query(root[x],ia,ib,0,n);
return ans;
}
int query(int x,int y,int ia,int ib){
return query(y,ia,ib)-query(x-1,ia,ib);
}
}bit;
void solve(int l,int r,int x){//将[l,r]置为x
auto lp=--ra.lower_bound(l+1),rp=ra.upper_bound(r),tmp=lp;//左闭右开
if(*lp!=l) p[a[*lp]].insert(l),pre[l]=l-1,a[l]=a[*lp],lp=ra.insert(l).first;//分裂左端点所在区间
if(*rp!=r+1) p[a[*prev(rp)]].insert(r+1),pre[r+1]=r,a[r+1]=a[*prev(rp)],rp=ra.insert(r+1).first;//右端点
in[st[++top]=x]=1;//st记录修改区间右侧需要更新的颜色
for(bool f=1;lp!=rp;ra.erase(lp++)){//lp=ra.erase(lp)也可以
p[a[*lp]].erase(*lp);
bit.chp(*lp,pre[*lp],-1);
if(f) f=0,bit.chp(*lp,pre[*lp]=((tmp=p[x].lower_bound(*lp))==p[x].begin()?0:*(ra.upper_bound(*(--tmp)))-1),1);
else bit.chp(*lp,pre[*lp]=*lp-1,1);//最左边的段需要查找前面的同色位置,其他段修改为i-1即可
if(!in[a[*lp]]) in[st[++top]=a[*lp]]=1;
a[*lp]=x;//由于每次访问都是在块的开头,所以更新也只操作块的开头元素即可
}
ra.insert(l),p[x].insert(l);
int c;
while(top){//处理修改区间右侧的pre
in[c=st[top--]]=0;
auto nxt=p[c].upper_bound(r);
if(nxt!=p[c].end()){
bit.chp(*nxt,pre[*nxt],-1);
bit.chp(*nxt,pre[*nxt]=((tmp=p[c].lower_bound(*nxt))==p[c].begin()?0:*(ra.upper_bound(*(--tmp)))-1),1);
}
}
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m,tn=n;
for(int i=1;i<=n;i++) cin>>a[i],b[i]=a[i];
for(int i=1,o;i<=m;i++){
cin>>o>>q[i].l>>q[i].r;
if(2-o) cin>>q[i].x,b[++tn]=q[i].x;
}
sort(b+1,b+1+tn),tn=unique(b+1,b+1+tn)-b-1;
for(int i=1;i<=tn;i++) ma[b[i]]=i;
for(int i=1;i<=n;i++){
a[i]=ma[a[i]];
bit.chp(i,pre[i]=lst[a[i]],1),lst[a[i]]=i;
if(a[i]!=a[i-1]) ra.insert(i),p[a[i]].insert(i);
}
ra.insert(0),ra.insert(n+1);
for(int i=1;i<=m;i++){
auto [l,r,x]=q[i];
if(l>r) continue;
if(x) solve(l,r,ma[x]);
else cout<<bit.query(l,r,0,l-1)<<"\n";
}
return 0;
}
solve() 是真的难写难调啊~~~ 疑似过于屎山了。
LOJ 上看到了实现出人意料简洁的代码,见 #1748229。虽然维护修改和查询的结构不是树套树而是 CDQ 分治,但是 set 维护的过程是共有的,如果有兴趣可以去学习一下。
小技巧
垃圾回收
防止 MLE,加上这个绝对不亏(如果中途有无用节点的话)。
但是一定要斟酌好删除条件。比如你的删除条件是 sum(x)==0,那你就要留心中途线段树是否可能出现负数从而导致误删。特殊地,若线段树在每次操作完都是正数,而操作过程中要处理减法,那你可以考虑将加法放在减法前面执行。
stack<int> gar;
void del(int &x){gar.push(x),x=0;}
void newnode(int &x){
if(!gar.empty()) x=gar.top(),gar.pop(),tr[x].init();
else x=++idx;
}
void chp(int& x,int a,int v,int l,int r){
if(!x) newnode(x);
sum[x]+=v;
if(l<r){
int mid=(l+r)>>1;
if(a<=mid) chp(lc[x],a,v,l,mid);
else chp(rc[x],a,v,mid+1,r);
}
if(删除条件...) del(x);
}
标记永久化
支持区间操作的线段树,其常数很大一部分来自标记下放 & 上传。
而且对于主席树上的区修操作,若是下放标记,会影响到之前的版本;若是所有涉及的节点都建新的,又可能爆空间(有结论,单次操作最多涉及 \(4\log n\) 个节点,这样几乎吃不消)。
标记永久化是一种不使用标记下放 / 上传技巧,即修改时将标记保留在修改节点处,并直接处理出该节点的答案,查询时额外累加标记的贡献。
void chr(int &x,int a,int b,int v,int l,int r){
x=clone(x);
sum(x)+=(b-a+1)*v;
if(a==l&&b==r) return tag(x)+=v,void();
int mid=(l+r)>>1;
if(b<=mid) chr(lc(x),a,b,v,l,mid);
else if(a>mid) chr(rc(x),a,b,v,mid+1,r);
else chr(lc(x),a,mid,v,l,mid),chr(rc(x),mid+1,b,v,mid+1,r);
}
int query(int x,int a,int b,int l,int r){
if(a==l&&b==r) return sum(x);
int mid=(l+r)>>1,sum=(b-a+1)*tag(x);
if(b<=mid) return sum+query(lc(x),a,b,l,mid);
else if(a>mid) return sum+query(rc(x),a,b,mid+1,r);
else return sum+query(lc(x),a,mid,l,mid)+query(rc(x),mid+1,b,mid+1,r);
}
注意到两个函数中,\(a,b\) 的值在最后一个 case 会与 \(l,r\) 一起变动。这是因为我们要想让 \([a,b]\) 始终 \(\subset [l,r]\),这样就能直接通过 \(b-a+1\) 来得出 \(|[a,b]\cap[l,r]|\),即当前区间被修改的元素个数,进而更方便地提前计算出此次修改对 sum(x) 的贡献。
模板题:SP11470 TTM - To the moon。
点击查看代码 R223037296
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10,M=1e5+10,logN=17;
int n,m,a[N],idx,root[N];
struct SEG{
int idx;
struct node{int lc,rc,sum,tag;}tr[(N+M)*logN<<2];
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define sum(x) (tr[x].sum)
#define tag(x) (tr[x].tag)
int clone(int x){return tr[++idx]=tr[x],idx;}
void build(int &x,int l,int r){
x=++idx;
if(l==r) return sum(x)=a[l],void();
int mid=(l+r)>>1;
build(lc(x),l,mid),build(rc(x),mid+1,r);
sum(x)=sum(lc(x))+sum(rc(x));
}
void chr(int &x,int a,int b,int v,int l,int r){
x=clone(x);
sum(x)+=(b-a+1)*v;
if(a==l&&b==r) return tag(x)+=v,void();
int mid=(l+r)>>1;
if(b<=mid) chr(lc(x),a,b,v,l,mid);
else if(a>mid) chr(rc(x),a,b,v,mid+1,r);
else chr(lc(x),a,mid,v,l,mid),chr(rc(x),mid+1,b,v,mid+1,r);
}
int query(int x,int a,int b,int l,int r){
if(a==l&&b==r) return sum(x);
int mid=(l+r)>>1,sum=(b-a+1)*tag(x);
if(b<=mid) return sum+query(lc(x),a,b,l,mid);
else if(a>mid) return sum+query(rc(x),a,b,mid+1,r);
else return sum+query(lc(x),a,mid,l,mid)+query(rc(x),mid+1,b,mid+1,r);
}
}tr;
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i],a[i]+=a[i-1];
char op;
for(int i=1,l,r,x;i<=m;i++){
cin>>op;
if(op=='C'){
cin>>l>>r>>x;
idx++,root[idx]=root[idx-1];
tr.chr(root[idx],l,r,x,1,n);
}else if(op=='Q'){
cin>>l>>r;
cout<<a[r]-a[l-1]+tr.query(root[idx],l,r,1,n)<<"\n";
}else if(op=='H'){
cin>>l>>r>>x;
cout<<a[r]-a[l-1]+tr.query(root[x],l,r,1,n)<<"\n";
}else{
cin>>x;
idx=x;
}
}
}
内外反套
内外反套,即将外层结构和内层结构维护的维度反过来。这个在上文 P3332 [ZJOI2013] K 大数查询中进行了说明。
内外反套,一般可以将本应树状数组来维护的区间操作,丢给内层线段树,避免较大的码量带来的调试困难(只是,经不完全测试,时间上可能略。略。略。逊一点)。
后缀树状数组
上文 P4093 [HEOI2016 / TJOI2016] 序列中我们利用了“最小值的查询是一个前缀”,从而避开了最值不可减的缺陷。
如果查询是一个后缀,我们则可以使用后缀树状数组,查询时 \(x\) 从 \(1\) 开始递增,修改时 \(x\) 从 \(n\) 开始递减。这样维护的就是后缀的信息了~
这样写还可以在顺序遍历的情况下,不作差地求逆序对。
如何避免漏写 root[] 导致的错误
动态开点线段树添加节点时,我们一般用 root[x] 来存储树状数组第 \(x\) 位对应的线段树的根节点。不过有时候我们可能会忘记加 root[],直接将 x 提供进去(至少我有时会这样 (^^;
为了解决这个问题,除了一遍遍提醒自己以外,还有另外一种方式(是我从 zhoukangyang 大佬的代码中学到的)。
如果根节点数量为 \(n\),那么 \(idx\) 就从 \(n+1\) 开始用,这样我们可以直接用 \(x\) 来代表根节点。不过相应地修改函数不能传引用进去,需要进行一些修改。
void newnode(int &x){if(!x) x=++idx;return idx;}
void chp(int x,int a,int v,int l,int r){
sum(x)+=v;
if(l==r) return;
int mid=(l+r)>>1;
if(a<=mid) chp(newnode(lc(x)),a,v,l,mid);
else chp(newnode(rc(x)),a,v,mid+1,r);
}
根据个人习惯来选择就好。
后
参考文章:
- 浅谈树状数组套权值树 by BFqwq
- 树状数组套权值树学习笔记 by LPF'sBlog
- P4175 题解 by jiqimao
你觉得数据结构可爱嘛?


 浙公网安备 33010602011771号
浙公网安备 33010602011771号