[题解]AtCoder Beginner Contest 410(ABC410) A~G
A - G1
统计有多少个\(a_i\ge k\)即可。
时间复杂度\(O(n)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e2+10;
int n,a[N],k,ans;
signed main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
cin>>k;
for(int i=1;i<=n;i++) ans+=(a[i]>=k);
cout<<ans<<"\n";
}
B - Reverse Proxy
模拟即可。
时间复杂度\(O(n)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e2+10;
int n,q,a[N];
signed main(){
cin>>n>>q;
while(q--){
int x;
cin>>x;
if(x){
a[x]++;
cout<<x<<"\n";
}else{
int minn=1e8,p=-1;
for(int i=1;i<=n;i++){
if(a[i]<minn) minn=a[i],p=i;
}
a[p]++;
cout<<p<<"\n";
}
}
return 0;
}
C - Rotatable Array
下面规定下标从\(0\)开始。
不难发现,经过\(x\)次移动操作后,新序列的第\(p\)位即为原序列的第\((p+x)\bmod n\)位。
因此不需要模拟移动的过程,仅需记录这个\(x\)即可。
时间复杂度\(O(q)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,q,x,a[N];
signed main(){
cin>>n>>q;
for(int i=0;i<n;i++) a[i]=i+1;
while(q--){
int op,p,k;
cin>>op;
if(op==1){
cin>>p>>k,p--;
a[(p+x)%n]=k;
}else if(op==2){
cin>>p,p--;
cout<<a[(p+x)%n]<<"\n";
}else{
cin>>k;
x=(x+k)%n;
}
}
}
D - XOR Shortest Walk
BFS即可。中途记录下当前节点的编号和截至目前的异或和。
最后输出能到达\(n\)的最大异或和即可,若达不到输出-1。
由于状态数量是\(nV\),时间复杂度也是\(O(nV)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10,V=1<<10;
int n,m;
struct edge{int to,w;};
bitset<N> vis[V];
vector<edge> G[N];
queue<pair<int,int>> q;
void add(int u,int v,int w){G[u].emplace_back(edge{v,w});}
signed main(){
cin>>n>>m;
for(int i=1,u,v,w;i<=m;i++) cin>>u>>v>>w,add(u-1,v-1,w);
q.push({0,0}),vis[0][0]=1;
while(!q.empty()){
auto t=q.front();
q.pop();
for(auto i:G[t.first]){
int ww=t.second^i.w;
if(vis[i.to][ww]) continue;
vis[i.to][ww]=1,q.push({i.to,ww});
}
}
for(int i=0;i<V;i++) if(vis[n-1][i]) cout<<i<<"\n",exit(0);
cout<<"-1\n";
return 0;
}
E - Battles in a Row
注意:必须按顺序打怪兽,中途某个怪兽打不过游戏就结束。
如果令\(f[i][j]\)表示“体力值剩下\(i\),魔法值剩下\(j\),能进行的最多轮数”的话,因为缺失当前的轮数,无法判断哪些状态是已经游戏结束的,难以递推。
因此考虑令\(f[i][j]\)表示“进行完第\(i\)轮,体力值还剩下\(j\),魔法值可能的最大值”。
初始除了\(f[0][H]=M\)之外,其他位置全都是\(-\infty\)。
则有转移\(f[i][j]=\max(f[i-1][j+a[i]],f[i-1][j]-b[i])\)。
最后找到\(f\)中非负值存在的最大行数,即为答案。
时间复杂度\(O(nH)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e3+10,M=3e3+10;
int n,h,m,f[N][M],a[N],b[N];
signed main(){
cin>>n>>h>>m;
for(int i=1;i<=n;i++) cin>>a[i]>>b[i];
memset(f,-0x3f,sizeof f);
f[0][h]=m;
for(int i=1;i<=n;i++){
for(int j=0;j<=h;j++){
f[i][j]=f[i-1][j]-b[i];
if(j+a[i]<=h) f[i][j]=max(f[i][j],f[i-1][j+a[i]]);
}
}
for(int i=n;i>=0;i--)
for(int j=0;j<=h;j++)
if(f[i][j]>=0) cout<<i,exit(0);
return 0;
}
F - Balanced Rectangles
下文中规定输入矩阵为\(n\times m\)的。
考虑枚举这个矩形的左右边缘\(l,r\),对于每个\((l,r)\),令\(b[x]\)表示“第\(1\)行到第\(x\)行”与“第\(l\)列到第\(r\)列”截成的矩形中有多少个#。
那么这对\((l,r)\)对答案的贡献即为:
(其中\([P]\)是艾弗森括号,\(P\)成立为\(1\),\(P\)不成立为\(0\)。)
括号中的:
变形即得:
令\(c[x]=2\times b[x]-x\times (r-l+1)\),上式即为:
由于\(i-1<j\),所以只需要统计\(c\)中有多少\(x<y\)使得\(c[x]=c[y]\),作为\((l,r)\)对答案的贡献。
这一步可以通过桶数组做到\(O(n)\)。
时间复杂度为\(O(m^2\times n)=O(mS)\),其中\(S\)为输入矩阵元素总数。
这样子如果\(m=S\),会被卡成\(O(S^2)\)。
因此如果\(m>n\)需要将输入转置一下,这样时间复杂度上界是\(O(S\sqrt S)\approx 1.6\times 10^8\),3s时限大概够了。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e5+10;
int t,n,m,b[N],cnt[N<<1],ans;
string tmp[N],s[N];
vector<int> a[N];
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr),cout.tie(nullptr);
cin>>t;
while(t--){
ans=0;
cin>>n>>m;
for(int i=0;i<n;i++) cin>>tmp[i];
if(n<m){//转置
swap(n,m);
for(int i=1;i<=n;i++){
s[i].resize(m+1);
for(int j=1;j<=m;j++){
s[i][j]=tmp[j-1][i-1];
}
}
for(int i=0;i<m;i++) tmp[i].clear();
}else{
for(int i=1;i<=n;i++){
s[i].resize(m+1);
for(int j=1;j<=m;j++){
s[i][j]=tmp[i-1][j-1];
}
}
for(int i=0;i<n;i++) tmp[i].clear();
}
for(int i=1;i<=n;i++){//处理前缀和
a[i].resize(m+1);
for(int j=1;j<=m;j++){
a[i][j]=a[i][j-1]+(s[i][j]=='#');
}
}
for(int i=1;i<=m;i++){
for(int j=i;j<=m;j++){
for(int k=1;k<=n;k++) b[k]=b[k-1]+a[k][j]-a[k][i-1];
for(int k=1;k<=n;k++) b[k]=(b[k]<<1)-k*(j-i+1);
for(int k=0;k<=n;k++) ans+=cnt[b[k]+N],cnt[b[k]+N]++;
for(int k=0;k<=n;k++) cnt[b[k]+N]=0;
}
}
cout<<ans<<"\n";
for(int i=1;i<=n;i++) a[i].clear(),s[i].clear();
}
return 0;
}
G - Longest Chord Chain
我们将环展开成链,在答案最优的情况下,一定存在一种保留方式形如下图:
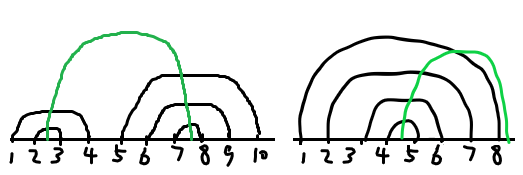
其中要保留的弦为黑色,添加的新弦为绿色。
可以发现,被保留的线段一定构成\(1\)或\(2\)个不交的区间,且每个区间的线段必须是层层嵌套的关系。而答案即为保留线段的最多条数。
如果只有\(1\)个区间,不难发现,按\(l\)从小到大排序后,所求的答案就是\(r\)的最长下降子序列。
对于\(2\)个区间的情况,官方题解的思路是分类讨论+线段树。不过我们有另一种方法,可以将\(2\)个区间转化成\(1\)个区间的问题。
对于线段\((l,r)\),我们也可以将其看作从\(r\)开始经过\(n\)又回到\(l\),因此我们扩张一下链的范围,在\((r,l+n)\)也连一条线段(蓝色):
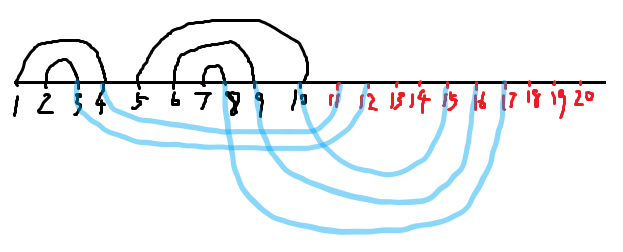
这样不难发现,之前的\(2\)个区间一定可以用这个新链上\(1\)个区间来表示。
又因为\((l,r),(r,l+n)\)不可能同时产生贡献,所以不会出现重复统计的问题。
至此就转化成了\(1\)个区间的问题。将\(l\)排序后求\(r\)的最长下降子序列即可。
时间复杂度\(O(n\log n)\)。
最长下降子序列属于线性dp的一类,可以参照此文章。
点击查看代码
#include<bits/stdc++.h>
#define N 200010
using namespace std;
struct Chord{int l,r;}c[N<<1];
int n,idx,f[N<<1],len;
bool cmp(int a,int b){return a>=b;}
signed main(){
cin>>n;
for(int i=1,l,r;i<=n;i++){
cin>>l>>r;
if(l>r) swap(l,r);
c[++idx]={l,r},c[++idx]={r,l+2*n};
}
sort(c+1,c+1+idx,[](Chord a,Chord b){return a.l<b.l;});
f[0]=INT_MAX;
for(int i=1;i<=idx;i++){
if(c[i].r<f[len]) f[++len]=c[i].r;
else f[lower_bound(f+1,f+1+len,c[i].r,cmp)-f]=c[i].r;
}
cout<<len<<"\n";
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号