[题解]LOJ6160 「美团 CodeM 初赛 Round A」二分图染色

#6160. 「美团 CodeM 初赛 Round A」二分图染色

转化一下题意：

定义一个\(n\times n\)的棋盘，如果左侧的\(i\)与右侧的\(j\)之间有一条红色的边，那么棋盘的\((i,j)\)处就放一个红色棋子；蓝色同理；绿色相当于不放。

要求每个格子最多放\(1\)个棋子，红色棋子之间不能同行同列，蓝色棋子之间不能同行同列。

先考虑如果只有\(1\)种颜色的棋子，答案是多少。

定义\(f(x)\)表示\(x\times x\)的网格只放一种颜色的棋子，满足条件的方法有多少种。

不难发现\(f(x)=\sum\limits_{i=0}^x C_x^i A_x^i\)。

---

如果有\(2\)种颜色，不能简单地将答案考虑为\(f(n)^2\)，因为这样可能会有一个格子放\(2\)种棋子的情况。

考虑使用容斥。最终答案即为“恰好\(0\)个格子有\(2\)种棋子”的方案数。

我们求“至少\(k\)个格子有\(2\)种棋子”的方案数是简单的，即为：

\[C_n^k A_n^k f(n-k)^2 \]

解释：\(C_n^k A_n^k\)是我们先任选了\(k\)个格子，钦定这些格子一定放\(2\)种棋子。然后我们删除放棋子的行和列，剩下的是一个\(n-k\)阶的棋盘，随便填即可，有\(f(n-k)^2\)种填法。

那么“恰好\(0\)个格子有\(2\)种棋子”的方案数，就是：

• $\ \ \ $“至少\(0\)个格子有\(2\)种棋子”的方案数
• \(-\)“至少\(1\)个格子有\(2\)种棋子”的方案数
• \(+\)“至少\(2\)个格子有\(2\)种棋子”的方案数
• \(-\)“至少\(3\)个格子有\(2\)种棋子”的方案数
• \(\dots\)

upd 2025/7/3：“至少\(k\)个格子有\(2\)种棋子”的方案数是有问题的，这样会有重复统计。至于答案为什么是下面的式子，等我学了容斥再回头考虑(^^;

也就是：

\[ans=\sum\limits_{i=0}^n (-1)^i C_n^i A_n^i f(n-i)^2 \]

---

然而我们发现瓶颈在于预处理\(f(0),f(1),\dots,f(n)\)是\(O(n^2)\)的，无法接受。

考虑能否在“棋盘”上分析出\(f\)的递推式，这样就可以在\(O(n)\)的复杂度内解决了。

考虑我们已经求出了\(f(0),f(1),\dots,f(x-1)\)，现在我们给\(x-1\)阶的棋盘添加一行一列：

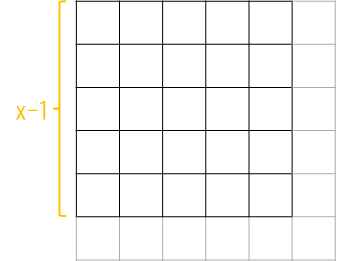
定义新增的区域内放置的棋子为“第一个棋子”，则：

• 如果不放置第一个棋子，贡献为\(f(x-1)\)。
• 如果放置第一个棋子，有\(2x-1\)种放法。
  
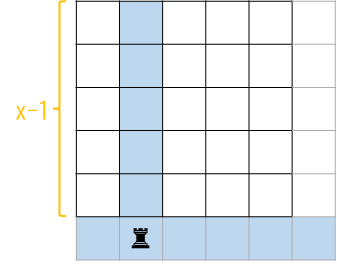
  以上图的放法为例，该棋子所在的行列（蓝色区域）都不能再放置棋子。白色部分有\(f(x-1)\)种填写方案。所以总贡献为\((2x-1)\times f(x-1)\)。

加起来即可得：

\[f(x)=2x\times f(x-1) \]

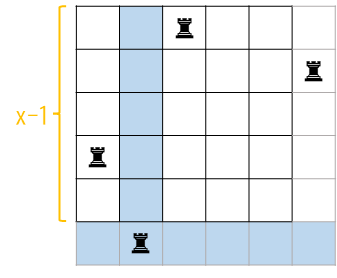
不过我们发现，这样子是有重复统计的。拿上图举个例子：

在\(f(x-1)\)种填法里，一定有一种是这样的：

如果我们一开始选择另外一个棋子作为“第一个棋子”：

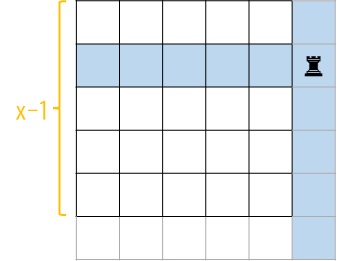
在它的\(f(x-1)\)种填法里，一定有一种是这样的：

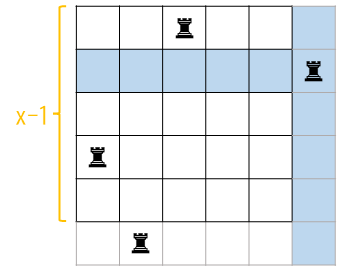
我们发现相同的答案被统计了\(2\)遍。

我们画出Venn图来了解统计答案的过程：

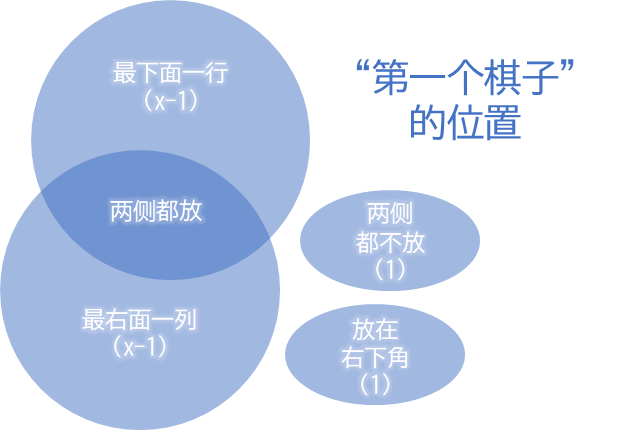
“两侧都放”这一情况，在下面和右面各被统计了一次。

因此为了避免重复，我们仅需限制：

• 第一个棋子放在最下面一行（除右下角）时，白色区域的最右边一列不能放置棋子。

白色区域最右边一列一共有\(x-1\)个位置，每个位置被放置棋子的方案数是\(f(x-2)\)（类比上面理解），且它们是两两互斥的。

因此一共需要减去\((x-1)^2\times f(x-2)\)种答案。

最终得出递推式：

\[f(x)=2x\times f(x-1)-(x-1)^2\times f(x-2) \]

---

总时间复杂度\(O(n)\)。

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define N 10000010
#define P 1000000007
using namespace std;
int n,inv[N],Cn[N],f[N],ans;
signed main(){
	cin>>n;
	Cn[0]=inv[1]=1;
	f[0]=1,f[1]=2;
	for(int i=2;i<=n;i++) inv[i]=(-P/i*inv[P%i]%P+P)%P;
	for(int i=1;i<=n;i++) Cn[i]=Cn[i-1]*(n-i+1)%P*inv[i]%P;
	for(int i=2;i<=n;i++) f[i]=(2*i*f[i-1]%P-(i-1)*(i-1)%P*f[i-2]%P+P)%P;
	for(int i=0,fac=1;i<=n;i++){
		if(i) fac=fac*i%P;
		(ans+=((i&1)?-1:1)*Cn[i]*Cn[i]%P*fac%P*f[n-i]%P*f[n-i]%P)%=P;
	}
	(ans+=P)%=P;
	cout<<ans<<"\n";
	return 0;
}