[笔记]线段树合并
线段树合并,就是将两棵线段树对应位置相加,得到一棵新的线段树。
由于实际应用中,通常要对很多棵线段树进行多次合并,所以和主席树类似地,我们使用动态开点线段树来实现。
算法概述
线段树合并的代码实现如下:
int merge(int x,int y,int l,int r){//将x,y为根的树都合并到x上
if(!x||!y) return x+y;//如果x=y=0则返回空节点,x=0则返回y,如果y=0则返回x
if(l==r) return sum(x)+=sum(y),x;
int mid=(l+r)>>1;
lc(x)=merge(lc(x),lc(y),l,mid);
rc(x)=merge(rc(x),rc(y),mid+1,r);
return pushup(x),x;
}
也可以通过引用改成void类型的:
void merge(int& x,int y,int l,int r){
if(!x||!y) return x+=y,void();
if(l==r) return sum(x)+=sum(y),void();
int mid=(l+r)>>1;
merge(lc(x),lc(y),l,mid);
merge(rc(x),rc(y),mid+1,r);
pushup(x);
}
下文规定\(T_1+T_2\)为线段树\(T_1,T_2\)合并后的结果,\(|T|\)表示线段树\(T\)的节点数。
关于线段树合并的时间复杂度,有结论:
- 对于\(n\)棵线段树\(T_1,T_2,\dots,T_n\),将它们合并的时间复杂度是\(O(\sum\limits_{i=1}^n |T_i|-|\sum\limits_{i=1}^n T_i|)\)。
下面的内容来自算法学习笔记(88): 线段树合并 by Pecco。
使用归纳法证明:
- 当\(n=0\)时,时间复杂度为\(O(0)\)。
- 假如对于\(n<k\)都成立,当\(n=k\)时,将\(T_1,T_2,\dots,T_n\),划分成两个非空集合\(S_1,S_2\)。
- 将\(S_1,S_2\)分别合并成\(T'_1,T'_2\),时间复杂度是:\[O(\sum\limits_{T\in S_1}|T|-|T'_1|)+O(\sum\limits_{T\in S_2}|T|-|T'_2|)\\=O(\sum\limits_{i=1}^n |T_i|-|T'_1|-|T'_2|) \]
- 再将\(T'_1,T'_2\)合并,根据代码可以发现时间复杂度就是两树重叠的节点个数,即:\[O(|T'_1|+|T'_2|-|T'_1+T'_2|) \]
\[O(\sum\limits_{i=1}^n |T_i|-|T'_1+T'_2|)\\=O(\sum\limits_{i=1}^n |T_i|-|\sum\limits_{i=1}^n T_i|) \] - 将\(S_1,S_2\)分别合并成\(T'_1,T'_2\),时间复杂度是:
所以,对于值域为\(n\)的若干线段树,如果对其进行了\(k\)次单点修改,总节点数是\(O(k\log n)\)的,合并它们的时间复杂度是\(O(k\log n-|\sum\limits_{i=1}^n T_i|)<O(k\log n)\)。
例题(题单点这里)
1. P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并
在树上进行若干条路径的区间修改(静态),我们通常使用树上差分。
举个例子,对于一棵树,想要给\(u\)到\(v\)路径上的每个节点增加\(k\),就相当于在该树的差分数组上进行如下操作:
- \(u\)处增加\(k\)。
- \(v\)处增加\(k\)。
- \(\text{LCA}(u,v)\)处减少\(k\)。
- \(fa[\text{LCA}(u,v)]\)处减少\(k\)。
将差分数组\(b\)还原成原数组\(a\),仅需令\(a[u]=(\sum\limits_{fa[v]=u} a[v])+b[u]\)即可。
我们给每个节点建一个值域为\(V\)的线段树,位置\(i\)上的值表示救济粮\(i\)有多少袋。
对于每次操作,按照上面的过程进行\(4\)次单点修改。
完成所有操作后,搜索每个节点\(u\),按上面的过程求出\(u\)还原后的线段树形态,此时\(u\)点的答案即为该线段树中最大值所在的下标。
不过这里我们要累加的不是整数,而是若干颗线段树,这就要用到线段树合并。
时间复杂度为\(O(m\log V)\)。
注意节点总数是\(4m\log V\approx 1.6\times 10^6\),因为单点修改次数是\(4m\)。
点击查看代码
#include<bits/stdc++.h>
#define N 100010
#define M 100010
#define V 100010
using namespace std;
struct edge{int nxt,to;}e[M<<1];
struct SEG{
struct node{int lc,rc,maxx,pos;}tr[M*80];//4MlogV
int idx;
#define lc(x) (tr[x].lc)//请注意,不使用undef的话,define的作用域是从此处直到文件结尾
#define rc(x) (tr[x].rc)//放在这里面只是为了条理一些
#define maxx(x) (tr[x].maxx)
#define pos(x) (tr[x].pos)
void pushup(int x){
maxx(x)=-1e9;
if(lc(x)&&maxx(lc(x))>maxx(x)) maxx(x)=maxx(lc(x)),pos(x)=pos(lc(x));
if(rc(x)&&maxx(rc(x))>maxx(x)) maxx(x)=maxx(rc(x)),pos(x)=pos(rc(x));
}
void chp(int &x,int a,int v,int l,int r){
if(!x) x=++idx;
if(l==r) return maxx(x)+=v,pos(x)=l,void();
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
pushup(x);
}
void merge(int &x,int y,int l,int r){
if(!x||!y) return x+=y,void();
if(l==r) return maxx(x)+=maxx(y),void();
int mid=(l+r)>>1;
merge(lc(x),lc(y),l,mid);
merge(rc(x),rc(y),mid+1,r);
pushup(x);
}
}tr;
int n,m,head[N],fa[N][20],dep[N],idx,root[N],ans[N];
void add(int u,int v){e[++idx]={head[u],v},head[u]=idx;}
void dfs(int u){
dep[u]=dep[fa[u][0]]+1;
for(int i=1;i<20;i++) fa[u][i]=fa[fa[u][i-1]][i-1];
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v!=fa[u][0]) fa[v][0]=u,dfs(v);
}
}
int LCA(int u,int v){
if(dep[u]<dep[v]) swap(u,v);
for(int i=19;~i;i--) if(dep[fa[u][i]]>=dep[v]) u=fa[u][i];
if(u==v) return u;
for(int i=19;~i;i--) if(fa[u][i]!=fa[v][i]) u=fa[u][i],v=fa[v][i];
return fa[u][0];
}
void dfs2(int u){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v!=fa[u][0]) dfs2(v),tr.merge(root[u],root[v],1,V);
}
if(tr.tr[root[u]].maxx) ans[u]=tr.tr[root[u]].pos;
}
signed main(){
cin>>n>>m;
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
add(u,v),add(v,u);
}
dfs(1);
for(int i=1,x,y,z,l;i<=m;i++){
cin>>x>>y>>z;
l=LCA(x,y);
tr.chp(root[x],z,1,1,V);
tr.chp(root[y],z,1,1,V);
tr.chp(root[l],z,-1,1,V);
tr.chp(root[fa[l][0]],z,-1,1,V);
}
dfs2(1);
for(int i=1;i<=n;i++) cout<<ans[i]<<"\n";
return 0;
}
2. P3605 [USACO17JAN] Promotion Counting P
相当于上道题的弱化版,仍然给每个节点建一个线段树(注意值域太大需要离散化)。
对于每个节点\(u\),将它到根节点的路径上每个节点对应的线段树上第\(p[u]\)位\(+1\),仍然使用树上差分来解决。
时间复杂度是\(O(n\log n)\)。
节点总数是\(n\log n\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define N 100010
using namespace std;
int n,nn,tmp[N],p[N],root[N],ans[N];
vector<int> G[N];
unordered_map<int,int> to;
struct SEG{
struct node{int lc,rc,sum;}tr[20*N];//nlogn
int idx;
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define sum(x) (tr[x].sum)
void pushup(int x){sum(x)=sum(lc(x))+sum(rc(x));}
void chp(int &x,int a,int v,int l,int r){
if(!x) x=++idx;
if(l==r) return sum(x)+=v,void();
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
pushup(x);
}
int query(int x,int a,int b,int l,int r){
if(a<=l&&r<=b) return sum(x);
int mid=(l+r)>>1,ans=0;
if(a<=mid) ans+=query(lc(x),a,b,l,mid);
if(b>mid) ans+=query(rc(x),a,b,mid+1,r);
return ans;
}
void merge(int &x,int y,int l,int r){
if(!x||!y) return x+=y,void();
if(l==r) return sum(x)+=sum(y),void();
int mid=(l+r)>>1;
merge(lc(x),lc(y),l,mid);
merge(rc(x),rc(y),mid+1,r);
pushup(x);
}
}tr;
void dfs(int u){
for(int i:G[u]) dfs(i),tr.merge(root[u],root[i],1,nn);
ans[u]=tr.query(root[u],to[p[u]]+1,nn,1,nn);
tr.chp(root[u],to[p[u]],1,1,nn);
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>p[i],tmp[i]=p[i];
sort(tmp+1,tmp+1+n);
nn=unique(tmp+1,tmp+1+n)-tmp-1;
for(int i=1;i<=nn;i++) to[tmp[i]]=i;
nn++;//哨兵节点
for(int i=2,u;i<=n;i++) cin>>u,G[u].emplace_back(i);
dfs(1);
for(int i=1;i<=n;i++) cout<<ans[i]<<"\n";
return 0;
}
3. CF600E Lomsat gelral
和上道题类似,不过线段树要维护的东西变成了最大值所在的下标之和,对pushup()进行一些修改即可;不需要离散化。
时间复杂度\(O(n\log V)=O(n\log n)\)。
节点总数是\(n\log V=n\log n\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define N 100010
using namespace std;
int n,ans[N],root[N];
vector<int> G[N];
struct SEG{
struct node{int lc,rc,maxx,ans;}tr[20*N];//nlogV=nlogn
int idx;
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define maxx(x) (tr[x].maxx)
#define ans(x) (tr[x].ans)
void pushup(int x){
if(maxx(lc(x))>maxx(rc(x))) maxx(x)=maxx(lc(x)),ans(x)=ans(lc(x));
else if(maxx(lc(x))<maxx(rc(x))) maxx(x)=maxx(rc(x)),ans(x)=ans(rc(x));
else maxx(x)=maxx(lc(x)),ans(x)=ans(lc(x))+ans(rc(x));
}
void chp(int &x,int a,int v,int l,int r){
if(!x) x=++idx;
if(l==r) return maxx(x)+=v,ans(x)=l,void();
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
pushup(x);
}
void merge(int &x,int y,int l,int r){
if(!x||!y) return x+=y,void();
if(l==r) return maxx(x)+=maxx(y),ans(x)=l,void();
int mid=(l+r)>>1;
merge(lc(x),lc(y),l,mid);
merge(rc(x),rc(y),mid+1,r);
pushup(x);
}
}tr;
void add(int u,int v){G[u].emplace_back(v);}
void dfs(int u,int fa){
for(int i:G[u]) if(i!=fa) dfs(i,u),tr.merge(root[u],root[i],1,n);
ans[u]=tr.tr[root[u]].ans;
}
signed main(){
cin>>n;
for(int i=1,c;i<=n;i++) cin>>c,tr.chp(root[i],c,1,1,n);
for(int i=1,u,v;i<n;i++) cin>>u>>v,add(u,v),add(v,u);
dfs(1,0);
for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
return 0;
}
4. P3521 [POI 2011] ROT-Tree Rotations
递归的过程中,逆序对只可能:
- 在左子树中。
- 在右子树中。
- 跨越左右子树。
如果前\(2\)种情况已经计算出来了,那么我们有\(2\)种决策:“交换左右子树”or“不交换左右子树”。
显然交不交换对只对第\(3\)种情况的答案有影响,所以我们可以贪心地取两种决策答案较小者。
至于如何计算两个子树之间的逆序对个数,可以为每个节点\(u\)开一个权值线段树,来表示子树\(u\)中每个数出现次数。
根据上面的分析,可以写出下面的代码:
int query(int x,int y,int l,int r){//子树x(左)和子树y(右)之间产生的逆序对数量
if(!x||!y) return 0;
if(l==r) return 0;
int mid=(l+r)>>1;
return query(lc(x),lc(y),l,mid)+query(rc(x),rc(y),mid+1,r)+sum(rc(x))*sum(lc(y));
}
将query()合并到merge()中即可在合并的同时求出两种决策的答案,在常数上有显著的效率提升。
时间复杂度是\(O(n\log V)=O(n\log n)\)。
节点总数是\(n\log V=n\log n\)。
此题有点卡空间,把不需要ll的变量尽量开int就好。
点击查看代码
#include<bits/stdc++.h>
#define ll long long
#define N 200010
using namespace std;
int n,idx;
ll ans,s1,s2;
struct SEG{
struct node{int lc,rc,sum;}tr[20*N];//nlogV=nlogn
int idx;
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define sum(x) (tr[x].sum)
void pushup(int x){sum(x)=sum(lc(x))+sum(rc(x));}
void chp(int &x,int a,int v,int l,int r){
if(!x) x=++idx;
if(l==r) return sum(x)+=v,void();
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
pushup(x);
}
void merge(int &x,int y,int l,int r){
if(!x||!y) return x+=y,void();
if(l==r) return sum(x)+=sum(y),void();
int mid=(l+r)>>1;
s1+=1ll*sum(lc(x))*sum(rc(y));
s2+=1ll*sum(rc(x))*sum(lc(y));
merge(lc(x),lc(y),l,mid);
merge(rc(x),rc(y),mid+1,r);
pushup(x);
}
}tr;
int dfs(){//由于节点编号是1~n的排列,所以直接用权值当编号
int p=0,x;
cin>>x;
if(!x){
int lc=dfs(),rc=dfs();
s1=s2=0,tr.merge(lc,rc,1,n);
p=lc,ans+=min(s1,s2);
}else tr.chp(p,x,1,1,n);
return p;
}
signed main(){
cin>>n;
dfs();
cout<<ans<<"\n";
return 0;
}
5.CF208E Blood Cousins
节点\(u\)的线段树的第\(i\)位存储“子树\(u\)中,深度为\(i\)的节点个数”。
对于询问“节点\(v\)有多少个\(p\)级表亲”,在\(u\)的\(k\)级祖先处统计贡献即可。贡献为线段树上\(dep[v]\)处的值。
时间复杂度是\(O((n+q)\log n)\)。
节点总数是\(n\log n\)。
点击查看代码
#include<bits/stdc++.h>
#define eb emplace_back
#define N 100010
#define Q 100010
using namespace std;
int n,q,r[N],dep[N],root[N],fa[N][20],ans[Q];
vector<int> G[N];
struct Que{int id,d;};
vector<Que> que[N];
struct SEG{
struct node{int lc,rc,sum;}tr[20*N];//nlogn
int idx;
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define sum(x) (tr[x].sum)
void pushup(int x){sum(x)=sum(lc(x))+sum(rc(x));}
void chp(int &x,int a,int v,int l,int r){
if(!x) x=++idx;
if(l==r) return sum(x)+=v,void();
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
pushup(x);
}
int query(int x,int a,int l,int r){
if(l==r) return sum(x);
int mid=(l+r)>>1;
if(a<=mid) return query(lc(x),a,l,mid);
else return query(rc(x),a,mid+1,r);
}
void merge(int &x,int y,int l,int r){
if(!x||!y) return x+=y,void();
if(l==r) return sum(x)+=sum(y),void();
int mid=(l+r)>>1;
merge(lc(x),lc(y),l,mid);
merge(rc(x),rc(y),mid+1,r);
pushup(x);
}
}tr;
void dfs(int u){
dep[u]=dep[fa[u][0]]+1;
for(int i=1;i<20;i++) fa[u][i]=fa[fa[u][i-1]][i-1];
for(int i:G[u]) fa[i][0]=u,dfs(i);
}
int kthp(int u,int k){
for(int i=0;i<20;i++) if((k>>i)&1) u=fa[u][i];
return u;
}
void dfs2(int u){
if(!u){for(int i:G[u]) dfs2(i);return;}
tr.chp(root[u],dep[u],1,1,n);
for(int i:G[u]){
dfs2(i);
tr.merge(root[u],root[i],1,n);
}
for(Que i:que[u]) ans[i.id]=tr.query(root[u],i.d,1,n)-1;
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>r[i],G[r[i]].eb(i);
cin>>q;
dep[0]=-1,dfs(0);
for(int i=1,x,y;i<=q;i++) cin>>x>>y,que[kthp(x,y)].eb(Que{i,dep[x]});
dfs2(0);
for(int i=1;i<=q;i++) cout<<ans[i]<<" ";
return 0;
}
6.P5384 [Cnoi2019] 雪松果树
和5.的题意相同。存在\(O(n)\)的DFS+差分做法,然后此题就卡线段树合并了。跳过。
7.P3899 [湖南集训] 更为厉害
对于询问\((p,k)\),答案有\(2\)种情况,分别统计:
- \(b\)是\(a\)的祖先:\(b\)在\(a\)以上\(k\)个节点内任意选择,\(c\)在子树\(a\)中任意选择。
贡献为:\(\min(dis(a,1),k)\times(siz[a]-1)\)。 - \(a\)是\(b\)的祖先:\(b\)在子树\(a\)中任意选择,\(c\)在子树\(b\)中任意选择。
贡献为:\(\sum\limits_{a是b的祖先,dis(a,b)\le k}(siz[b]-1)\)。
其中统计后面的式子,可以每个节点\(u\)开一个线段树,第\(i\)个位置表示深度为\(i\)且在\(u\)子树中的节点\(b\)的\((siz[b]-1)\)之和。
时间复杂度是\(O((n+q)\log n)\)。
节点总数是\(n\log n\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e5+10,Q=3e5+10;
struct SEG{
struct node{int lc,rc,sum;}tr[N*20];//nlogn
int idx;
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define sum(x) (tr[x].sum)
void pushup(int x){sum(x)=sum(lc(x))+sum(rc(x));}
void chp(int &x,int a,int v,int l,int r){
if(!x) x=++idx;
if(l==r) return sum(x)+=v,void();
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
pushup(x);
}
int query(int x,int a,int b,int l,int r){
if(a<=l&&r<=b) return sum(x);
int mid=(l+r)>>1,ans=0;
if(a<=mid) ans+=query(lc(x),a,b,l,mid);
if(b>mid) ans+=query(rc(x),a,b,mid+1,r);
return ans;
}
void merge(int &x,int y,int l,int r){
if(!x||!y) return x+=y,void();
if(l==r) return sum(x)+=sum(y),void();
int mid=(l+r)>>1;
merge(lc(x),lc(y),l,mid);
merge(rc(x),rc(y),mid+1,r);
pushup(x);
}
}tr;
struct Que{int id,k;};
int n,q,root[N],dep[N],siz[N],ans[Q];
vector<int> G[N];
vector<Que> que[N];
void add(int u,int v){G[u].emplace_back(v);}
void dfs(int u,int fa){
dep[u]=dep[fa]+1,siz[u]=1;
for(int i:G[u]) if(i!=fa) dfs(i,u),siz[u]+=siz[i];
}
void dfs2(int u,int fa){
for(int i:G[u]) if(i!=fa) dfs2(i,u),tr.merge(root[u],root[i],1,n);
for(Que i:que[u]){
ans[i.id]=tr.query(root[u],dep[u]+1,min(dep[u]+i.k,n),1,n)+(siz[u]-1)*min(dep[u]-1,i.k);
}
tr.chp(root[u],dep[u],siz[u]-1,1,n);
}
signed main(){
cin>>n>>q;
for(int i=1,u,v;i<n;i++) cin>>u>>v,add(u,v),add(v,u);
for(int i=1,p,k;i<=q;i++) cin>>p>>k,que[p].emplace_back(Que{i,k});
dfs(1,0),dfs2(1,0);
for(int i=1;i<=q;i++) cout<<ans[i]<<"\n";
return 0;
}
8.CF1009F Dominant Indices
节点\(u\)的线段树的第\(i\)位表示“\(u\)子树内有多少个节点深度为\(i\)”。
其答案为该线段树内“最大值出现的最小下标”,有两种实现方法:
- 记录\(maxx,mpos\)分别表示最大值和最大值所在最小下标,然后正常转移。
- 仅记录\(maxx\),然后使用线段树上二分。
后者代码实现和时空占用上都更优,两种方法的具体实现详见代码。
此题有点卡线段树合并,所以需要节点回收。
具体来说,在线段树合并时,将\(T_B\)合并到\(T_A\)上之后,\(T_B\)中不被转移到\(T_A\)上的节点就用不上了(不排除需要使用这些节点的情况,不过此题和之前的题都不需要),所以在merge的过程中将这些节点压入一个栈,表示我们已经将它们回收。
在创建新节点时,我们优先从栈中取,如果栈是空的再用++idx开辟新节点。
这样不难发现任何时刻线段树中的节点数都不会超过\(n\)。
实际上前面的题都可以这样优化。
时间复杂度是\(O(n\log n)\)。
节点总数是\(n\log n\rightarrow n\)。
实现$1$
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,head[N],idx,dep[N],root[N],ans[N];
struct edge{int nxt,to;}e[N<<1];
void add(int u,int v){e[++idx]={head[u],v},head[u]=idx;}
struct SEG{
stack<int> gar;
struct Data{int maxx,mpos;};
struct Node{
int lc,rc;
Data data;
void init(){data={0,0},lc=rc=0;}
}tr[N];
Data add(Data a,Data b){
if(a.maxx<b.maxx) return {b.maxx,b.mpos};
else return {a.maxx,a.mpos};
}
int idx;
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define maxx(x) (tr[x].data.maxx)
#define mpos(x) (tr[x].data.mpos)
int newnode(){
int k;
if(!gar.empty()){
k=gar.top(),gar.pop();
}else k=++idx;
return tr[k].init(),k;
}
void pushup(int x){tr[x].data=add(tr[lc(x)].data,tr[rc(x)].data);}
void chp(int &x,int a,int v,int l,int r){
if(!x) x=newnode();
if(l==r) return maxx(x)+=v,mpos(x)=l,void();
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
pushup(x);
}
Data query(int x,int a,int b,int l,int r){
if(a<=l&&r<=b) return tr[x].data;
int mid=(l+r)>>1;
if(a<=mid&&b>mid) return add(query(lc(x),a,b,l,mid),query(rc(x),a,b,mid+1,r));
if(a<=mid) return query(lc(x),a,b,l,mid);
return query(rc(x),a,b,mid+1,r);
}
void merge(int &x,int y,int l,int r){
if(!x||!y) return x+=y,void();
gar.push(y);
if(l==r) return maxx(x)+=maxx(y),void();
int mid=(l+r)>>1;
merge(lc(x),lc(y),l,mid);
merge(rc(x),rc(y),mid+1,r);
pushup(x);
}
}tr;
void dfs(int u,int fa){
dep[u]=dep[fa]+1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v!=fa) dfs(v,u);
}
}
void dfs2(int u,int fa){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v!=fa) dfs2(v,u),tr.merge(root[u],root[v],1,n);
}
tr.chp(root[u],dep[u],1,1,n);
ans[u]=tr.query(root[u],dep[u],n,1,n).mpos-dep[u];
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr),cout.tie(nullptr);
cin>>n;
for(int i=1,u,v;i<n;i++) cin>>u>>v,add(u,v),add(v,u);
dfs(1,0),dfs2(1,0);
for(int i=1;i<=n;i++) cout<<ans[i]<<"\n";
return 0;
}
实现$2$
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,head[N],idx,dep[N],root[N],ans[N];
struct edge{int nxt,to;}e[N<<1];
void add(int u,int v){e[++idx]={head[u],v},head[u]=idx;}
struct SEG{
stack<int> gar;
struct Node{
int lc,rc,maxx;
void init(){lc=rc=maxx=0;}
}tr[N];
int idx;
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define maxx(x) (tr[x].maxx)
int newnode(){
int k;
if(!gar.empty()){
k=gar.top(),gar.pop();
}else k=++idx;
return tr[k].init(),k;
}
void pushup(int x){maxx(x)=max(maxx(lc(x)),maxx(rc(x)));}
void chp(int &x,int a,int v,int l,int r){
if(!x) x=newnode();
if(l==r) return maxx(x)+=v,void();
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
pushup(x);
}
int query(int x,int l,int r){
if(l==r) return l;
int mid=(l+r)>>1;
if(maxx(lc(x))==maxx(x)) return query(lc(x),l,mid);
else return query(rc(x),mid+1,r);
}
void merge(int &x,int y,int l,int r){
if(!x||!y) return x+=y,void();
gar.push(y);
if(l==r) return maxx(x)+=maxx(y),void();
int mid=(l+r)>>1;
merge(lc(x),lc(y),l,mid);
merge(rc(x),rc(y),mid+1,r);
pushup(x);
}
}tr;
void dfs(int u,int fa){
dep[u]=dep[fa]+1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v!=fa) dfs(v,u);
}
}
void dfs2(int u,int fa){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v!=fa) dfs2(v,u),tr.merge(root[u],root[v],1,n);
}
tr.chp(root[u],dep[u],1,1,n);
ans[u]=tr.query(root[u],1,n)-dep[u];
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr),cout.tie(nullptr);
cin>>n;
for(int i=1,u,v;i<n;i++) cin>>u>>v,add(u,v),add(v,u);
dfs(1,0),dfs2(1,0);
for(int i=1;i<=n;i++) cout<<ans[i]<<"\n";
return 0;
}
顺便推荐一下这篇文章:浅谈如何优美地实现线段树? by Creed-qwq。
这篇文章介绍了线段树的通用框架,在面对较复杂的信息维护下,能保证代码有很强的复用性,不用再写大量本质相同的代码。
实现\(1\)的线段树框架就部分参考了该文章(注意使用动态开点线段树的话,记录的左右孩子要独立于Data、Tag之外)。
8.CF570D Tree Requests
节点\(u\)的线段树的第\(i\)位表示“深度为\(i\)且在\(u\)子树中的节点上的字母的信息”。
显然我们只需要知道每个字母出现次数的奇偶性,因此我们可以把该信息压成一个整数,第\(i\)个二进制位表示第\(i\)个字母出现的次数的奇偶性。
合并时,将要合并的两个叶节点求异或即可。
本题中我们所要维护的仅有叶子结点的信息,因此不需要pushup。
时间复杂度\(O((n+q)\log n)\)。
节点总数是\(n\log n\)。
点击查看代码
#include<bits/stdc++.h>
#define eb emplace_back
#define pc __builtin_popcount
using namespace std;
const int N=5e5+10,Q=5e5+10;
int n,q,root[N],ans[Q],dep[N];
string s;
vector<int> G[N];
vector<pair<int,int>> que[N];
struct SEG{
struct node{int lc,rc,v;}tr[N*20];//nlogn
int idx;
#define lc(x) (tr[x].lc)
#define rc(x) (tr[x].rc)
#define v(x) (tr[x].v)
void chp(int &x,int a,int v,int l,int r){
if(!x) x=++idx;
if(l==r) return v(x)^=v,void();
int mid=(l+r)>>1;
if(a<=mid) chp(lc(x),a,v,l,mid);
else chp(rc(x),a,v,mid+1,r);
}
int query(int x,int a,int l,int r){
if(l==r) return v(x);
int mid=(l+r)>>1;
if(a<=mid) return query(lc(x),a,l,mid);
return query(rc(x),a,mid+1,r);
}
void merge(int &x,int y,int l,int r){
if(!x||!y) return x+=y,void();
if(l==r) return v(x)^=v(y),void();
int mid=(l+r)>>1;
merge(lc(x),lc(y),l,mid);
merge(rc(x),rc(y),mid+1,r);
}
}tr;
void dfs(int u){
for(int i:G[u]){
dep[i]=dep[u]+1,dfs(i);
tr.merge(root[u],root[i],1,n);
}
tr.chp(root[u],dep[u],(1<<(s[u]-'a')),1,n);
for(auto i:que[u]){
ans[i.first]=(pc(tr.query(root[u],i.second,1,n))<=1);
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(nullptr),cout.tie(nullptr);
cin>>n>>q;
for(int i=2,u;i<=n;i++) cin>>u,G[u].eb(i);
cin>>s,s=' '+s;
for(int i=1,u,d;i<=q;i++) cin>>u>>d,que[u].eb(i,d);
dep[1]=1,dfs(1);
for(int i=1;i<=q;i++) cout<<(ans[i]?"Yes\n":"No\n");
return 0;
}
8.P1600 [NOIP 2016 提高组] 天天爱跑步
参考:此文 by Engulf。
对于\((s,t)\)这条路径,考虑它对\(x\)节点产生贡献的情况:
-
\(x\)在\((s,\text{lca})\)上。
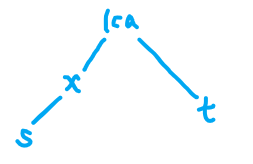
则有\(dep_s-dep_x=w_x\),即\(dep_s=dep_x+w_x\)。 -
\(x\)在\((\text{lca},t)\)上。
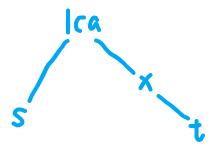
则有\((dep_\text{lca}-dep_s)+(dep_x-dep_\text{lca})=w_x\),即\(2\times dep_\text{lca}-dep_s=dep_x-w_x\)。
因此我们用两个线段树合并。
- 第一次,对于每个\((s_i,\text{lca}_i)\),将\(dep_s\)加入其上节点对应的权值线段树。对\(ans_x\)的贡献为\(dep_x+w_x\)处的值。
- 第二次,对于每个\((\text{lca}_i,t_i)\),将\(2\times dep_\text{lca}-dep_s\)加入其上节点对应的权值线段树。对\(ans_x\)的贡献为\(dep_x-w_x\)处的值。
由于修改都是针对链来进行的,所以于同理P4556,使用树上差分即可解决。
注意不要重复/漏统计\(\text{lca}\)。
时间复杂度\(O(n\log^2 n)\)。
节点总数懒得算了(逃
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+10;
int n,m,w[N],head[N],idx,root[N][2];
int dep[N],fa[N][20],mxdep,ans[N];
struct SEG{
int idx;
int lc[N*80],rc[N*80],s[N*80];
void pushup(int x){s[x]=s[lc[x]]+s[rc[x]];}
void chp(int &x,int a,int v,int l,int r){
if(!x) x=++idx;
if(l==r) return s[x]+=v,void();
int mid=(l+r)>>1;
if(a<=mid) chp(lc[x],a,v,l,mid);
else chp(rc[x],a,v,mid+1,r);
pushup(x);
}
int qry(int x,int a,int l,int r){
if(l==r) return s[x];
int mid=(l+r)>>1;
if(a<=mid) return qry(lc[x],a,l,mid);
return qry(rc[x],a,mid+1,r);
}
void merge(int &x,int y,int l,int r){
if(!x||!y) return x+=y,void();
if(l==r) return s[x]+=s[y],void();
int mid=(l+r)>>1;
merge(lc[x],lc[y],l,mid);
merge(rc[x],rc[y],mid+1,r);
pushup(x);
}
}tr;
struct Edge{int nxt,to;}e[N<<1];
void add(int u,int v){e[++idx]={head[u],v},head[u]=idx;}
void dfs(int u){
mxdep=max(mxdep,dep[u]=dep[fa[u][0]]+1);
for(int i=0;i<19;i++) fa[u][i+1]=fa[fa[u][i]][i];
for(int i=head[u],v;i;i=e[i].nxt)
if((v=e[i].to)!=fa[u][0]) fa[v][0]=u,dfs(v);
}
int LCA(int u,int v){
if(dep[u]<dep[v]) swap(u,v);
for(int i=19;~i;i--) if(dep[fa[u][i]]>=dep[v]) u=fa[u][i];
if(u==v) return u;
for(int i=19;~i;i--) if(fa[u][i]!=fa[v][i]) u=fa[u][i],v=fa[v][i];
return fa[u][0];
}
void dfs2(int u){
for(int i=head[u],v;i;i=e[i].nxt){
if((v=e[i].to)==fa[u][0]) continue;
dfs2(v);
tr.merge(root[u][0],root[v][0],1,mxdep);
tr.merge(root[u][1],root[v][1],-mxdep,mxdep<<1);
}
if(dep[u]+w[u]<=mxdep) ans[u]+=tr.qry(root[u][0],dep[u]+w[u],1,mxdep);
if(dep[u]-w[u]>=-mxdep) ans[u]+=tr.qry(root[u][1],dep[u]-w[u],-mxdep,mxdep<<1);
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1,u,v;i<n;i++) cin>>u>>v,add(u,v),add(v,u);
for(int i=1;i<=n;i++) cin>>w[i];
dfs(1);
for(int i=1,u,v,l;i<=m;i++){
cin>>u>>v,l=LCA(u,v);
tr.chp(root[u][0],dep[u],1,1,mxdep);
tr.chp(root[l][0],dep[u],-1,1,mxdep);
tr.chp(root[v][1],(dep[l]<<1)-dep[u],1,-mxdep,mxdep<<1);
tr.chp(root[fa[l][0]][1],(dep[l]<<1)-dep[u],-1,-mxdep,mxdep<<1);
}
dfs2(1);
for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
return 0;
}
\(\text{[Fin.]}\)

 浙公网安备 33010602011771号
浙公网安备 33010602011771号