[题解]AtCoder Beginner Contest 394(ABC394) A~G
A - 22222
遍历字符串\(s\),按题意输出所有2即可。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
string s;
signed main(){
cin>>s;
for(auto a:s) if(a=='2') cout<<a;
return 0;
}
B - cat
按题意模拟即可。
点击查看代码
#include<bits/stdc++.h>
#define N 60
using namespace std;
int n;
string s[N];
signed main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>s[i];
sort(s+1,s+1+n,[](string a,string b){
return a.size()<b.size();
});
for(int i=1;i<=n;i++) cout<<s[i];
return 0;
}
C - Debug
容易发现答案就是将原字符串所有形如WWW...WWWA的子串替换成ACCC...CCC,如此模拟即可得到答案。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
string s;
int n;
signed main(){
cin>>s;
n=s.size();
int pos=-1;
for(int i=0;i<n;i++){
if(s[i]=='W'){
if(pos==-1) pos=i;
}else if(s[i]=='A'){
if(~pos){
cout<<"A";
for(int j=pos;j<i;j++) cout<<"C";
pos=-1;
}else{
cout<<"A";
}
}else{
if(~pos){
for(int j=pos;j<i;j++) cout<<s[j];
pos=-1;
}
cout<<s[i];
}
}
if(~pos){
for(int j=pos;j<n;j++) cout<<s[j];
pos=-1;
}
return 0;
}
上面是赛时思路,稍有点繁琐。实际上不难发现,我们可以直接倒序遍历字符串,遇到WA便修改成AC。
这样做是正确的,因为每次修改只可能对之前的字符串产生影响。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
string s;
int n;
signed main(){
cin>>s,n=s.size();
for(int i=n-1;i>0;i--){
if(s[i]=='A'&&s[i-1]=='W'){
s[i]='C',s[i-1]='A';
}
}
cout<<s;
return 0;
}
D - Colorful Bracket Sequence
居然是括号匹配模板题w
具体过程如下,类似于模拟,所以正确性比较显然:
定义一个栈,初始为空。
对于\(i=1,2,\dots,n\),依次遍历\(s_i\):
- 如果\(s_i\)是左括号,将\(s_i\)入栈。
- 如果\(s_i\)是右括号,取出栈顶的左括号,看是否与\(s_i\)匹配。如果不匹配或者栈为空,断定
No。
如果最终栈非空,断定No,否则断定Yes。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
stack<char> st;
string s;
bool solve(){
for(char i:s){
if(i=='('||i=='['||i=='<'){
st.push(i);
}else{
if(st.empty()) return 0;
char c=st.top();
st.pop();
if(i==')'&&c!='(') return 0;
if(i==']'&&c!='[') return 0;
if(i=='>'&&c!='<') return 0;
}
}
return st.empty();
}
signed main(){
cin>>s;
cout<<(solve()?"Yes":"No");
return 0;
}
E - Palindromic Shortest Path
考虑到一个回文串的头尾各添加一个相同的字符,仍然是一个回文串,所以考虑使用BFS求解,队列里存的是形如\((u,v)\)的路径。
-
先对于\(i=1,2,\dots,n\),将长度为\(0\)的路径\((i,i)\)加入队列,并令\(ans_{i,i}=0\)。
-
再对于\((u,v)\in E\),将长度为\(1\)的路径\((u,v)\)加入队列,并令\(ans_{u,v}=1\)。
-
接下来进行BFS,对于从队头取出的\((x,y)\)这条路径,枚举\(1\le i,j\le n\),若同时满足:
- \(ans_{i,j}\)未被更新。
- \((i,x),(y,j)\in E\)。
- \((i,x),(y,j)\)
则令\(ans_{i,j}=ans_{x,y}+1\),并将\((i,j)\)入队。
由于我们保证队列中每个路径的\(ans\)从队头到队尾不降,所以\(ans_{i,j}\)第一次更新的值一定是最小的。自然正确性可以保证。
时间复杂度:最多\(O(n^2)\)次入队操作,枚举\(i,j\)是\(O(n^2)\)的。所以时间复杂度是\(O(n^4)\)。
点击查看代码
#include<bits/stdc++.h>
#define N 105
using namespace std;
int n,ans[N][N];
string a[N];
queue<pair<int,int>> q;
signed main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i],a[i]=' '+a[i];
memset(ans,-1,sizeof ans);
for(int i=1;i<=n;i++) ans[i][i]=0,q.push({i,i});
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)
if(i!=j&&a[i][j]!='-') ans[i][j]=1,q.push({i,j});
while(!q.empty()){
auto [x,y]=q.front();//注意 该写法仅c++17或以上可用
q.pop();
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)
if(ans[i][j]==-1&&a[i][x]==a[y][j]&&a[i][x]!='-')
ans[i][j]=ans[x][y]+2,q.push({i,j});
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++) cout<<ans[i][j]<<" ";
cout<<"\n";
}
return 0;
}
\(O(n^4)\)居然是正解,难道哪里跑不满吗……?
也存在\(O(n^3+26n^2)\)的做法,at上有题解,改天补。
F - Alkane
考虑树形dp。
由于一个烷烃只包含度为\(1,4\)的节点,当我们规定必须从子树\(u\)中选定一个包含\(u\)的连通块作为烷烃时,根据\(u\)的度数,可能的形态只有下面两种:
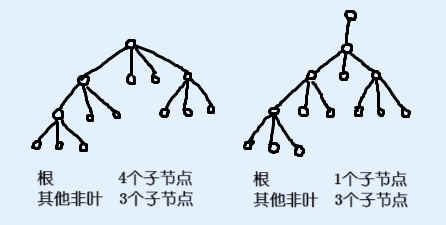
所以我们考虑计算一个\(f\)数组,其中\(f_u\)表示从子树\(u\)中选定一个包含\(u\)的最大连通块,使得它是一个严格三叉树(非叶节点都有\(3\)个子节点)时,该连通块的大小。
\(f_u\)的计算过程如下,其中\(ch\)表示\(u\)的子节点个数:
- 若\(ch<3\),\(f_u=1\)。
- 若\(ch\ge 3\),\(f_u=f_{i_1}+f_{i_2}+f_{i_3}+1\)。其中\(i_x\)表示\(u\)的子节点中,\(f\)值第\(x\)大的节点。
然后就是计算答案了,讨论上图中\(2\)种情况。对于节点\(u\):
- 若\(ch\ge 4\),有\(f_{i_1}+f_{i_2}+f_{i_3}+f_{i_4}+1\)的贡献,\(i\)的含义同上。
- 若\(ch\ge 3\),且\(u\)不是根节点,有\(f_{i_1}+f_{i_2}+f_{i_3}+2\)的贡献。
时间复杂度为\(O(n)\)。
代码将计算\(f\)和计算答案这\(2\)个步骤合在一起写了。
点击查看代码
#include<bits/stdc++.h>
#define N 200010
using namespace std;
int n,ans;
vector<int> G[N];
int dfs(int u,int fa){
int maxx[4]={0},ch=0;
for(int i:G[u]){
if(i==fa) continue;
int t=dfs(i,u);
ch++;
if(t>=maxx[0]) maxx[3]=maxx[2],maxx[2]=maxx[1],maxx[1]=maxx[0],maxx[0]=t;
else if(t>=maxx[1]) maxx[3]=maxx[2],maxx[2]=maxx[1],maxx[1]=t;
else if(t>=maxx[2]) maxx[3]=maxx[2],maxx[2]=t;
else if(t>=maxx[3]) maxx[3]=t;
}
if(ch<=2) return 1;
if(ch>=4) ans=max(ans,maxx[0]+maxx[1]+maxx[2]+maxx[3]+1);
if(u!=1) ans=max(ans,maxx[0]+maxx[1]+maxx[2]+2);
return maxx[0]+maxx[1]+maxx[2]+1;
}
signed main(){
cin>>n;
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
G[u].emplace_back(v);
G[v].emplace_back(u);
}
dfs(1,0);
cout<<(ans?ans:-1)<<"\n";
return 0;
}
G - Dense Buildings
发现答案的限制因素是始末两点间路径上,最矮的建筑。
为了使答案最优,我们要最大化这个建筑高度,所以这是一个最大瓶颈路问题。
我们根据输入建图,两点间的权值为它们高度的最小值。
然后跑原图的最大生成树,用LCA维护两点间的最小值,即为我们要最大化的建筑高度。
对于每个询问,设这个高度为\(h\),那么如果\(h\ge y\)或\(h\ge z\),则输出\(|y-z|\),否则输出\(y+z-2h\)。
注意特判始末位置相同的情况,输出\(|y-z|\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define H 505
#define W 505
#define N (H*W)
#define M (N<<2)
#define eb emplace_back
using namespace std;
struct edge{int to,w;};
struct _edge{int u,v,w;}e[M];
int n,m,q,l[H][W],idx,fa[N],f[N][20],minn[N][20],dep[N];
vector<edge> G[N];
void add(int u,int v,int w){G[u].eb(edge{v,w}),G[v].eb(edge{u,w});}
void eadd(int u,int v,int w){e[++idx]={u,v,w};}
int getid(int x,int y){return (x-1)*m+y;}
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
void dfs(int u){
dep[u]=dep[f[u][0]]+1;
for(int i=1;i<20;i++){
f[u][i]=f[f[u][i-1]][i-1];
minn[u][i]=min(minn[u][i-1],minn[f[u][i-1]][i-1]);
}
for(edge i:G[u]){
int v=i.to,w=i.w;
if(v==f[u][0]) continue;
f[v][0]=u,minn[v][0]=w,dfs(v);
}
}
int getmin(int u,int v){
int ans=LLONG_MAX;
if(dep[u]>dep[v]) swap(u,v);
for(int i=19;~i;i--) if(dep[f[v][i]]>=dep[u]) ans=min(ans,minn[v][i]),v=f[v][i];
if(u==v) return ans;
for(int i=19;~i;i--) if(f[v][i]!=f[u][i]) ans=min({ans,minn[u][i],minn[v][i]}),u=f[u][i],v=f[v][i];
return min({ans,minn[u][0],minn[v][0]});
}
signed main(){
memset(minn,0x3f,sizeof minn);
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>l[i][j];
if(i>1) eadd(getid(i,j),getid(i-1,j),min(l[i][j],l[i-1][j]));
if(j>1) eadd(getid(i,j),getid(i,j-1),min(l[i][j],l[i][j-1]));
}
}
for(int i=1;i<=n*m;i++) fa[i]=i;
sort(e+1,e+1+idx,[](_edge a,_edge b){return a.w>b.w;});
for(int i=1;i<=idx;i++){
int u=e[i].u,v=e[i].v;
u=find(u),v=find(v);
if(u==v) continue;
fa[u]=v,add(u,v,e[i].w);
}
dfs(1);
cin>>q;
while(q--){
int a,b,y,c,d,z;
cin>>a>>b>>y>>c>>d>>z;
if(getid(a,b)==getid(c,d)) cout<<abs(y-z)<<"\n";
else{
int v=getmin(getid(a,b),getid(c,d));
if(v>=y||v>=z) cout<<abs(y-z)<<"\n";
else cout<<y+z-2*v<<"\n";
}
}
return 0;
}
后
ABCDF。
E题一直考虑最短路一类的算法,比如Floyd转移时限制\((i,k)\)和\((k,j)\)的字符串恰好相反,但是显然很多细节都是无法处理的。是真没想到BFS,有点可惜。不过由于赛时很快略过去了,所以损失不大。
F题感觉水了,思路比较自然。
G题补题时一直想的最短路,看了题解瞬间明白了,算是还能做的G了(

 浙公网安备 33010602011771号
浙公网安备 33010602011771号