[题解]AtCoder Beginner Contest 385(ABC385) A~F

A - Equally

显然分组情况一定是\(1+1+1\)或\(1+2\)，直接判定即可。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int a,b,c;
signed main(){
	cin>>a>>b>>c;
	if((a+b==c)||(a+c==b)||(b+c==a)||(a==b&&b==c)) cout<<"Yes\n";
	else cout<<"No\n";
	return 0;
}

B - Santa Claus 1

照题意模拟即可。

点击查看代码

#include<bits/stdc++.h>
#define N 110
using namespace std;
int n,m,x,y,cnt;
string s[N],t;
bitset<N> vis[N];
signed main(){
	cin>>n>>m>>x>>y;
	for(int i=1;i<=n;i++){
		cin>>s[i];
		s[i]=' '+s[i];
	}
	cin>>t;
	for(int i:t){
		int xx=x,yy=y;
		if(i=='U') xx--;
		else if(i=='D') xx++;
		else if(i=='L') yy--;
		else yy++;
		if(xx<1||yy<1||xx>n||yy>m||s[xx][yy]=='#') continue;
		x=xx,y=yy;
		if(s[x][y]=='@'&&!vis[x][y]) vis[x][y]=1,cnt++;
	}
	cout<<x<<" "<<y<<" "<<cnt<<"\n";
	return 0;
}

C - Illuminate Buildings

DP，设\(f[i][j]\)为以\(i\)为结尾，上一个位置是\(i-j\)的答案数。

初始\(f\)全为\(1\)，转移显然有\(f[i][j]=\max(f[i][j],f[i-j][j]+1)\)，其中\(j\in [1,i]\)且\(a[i-j]=a[i]\)。

时间复杂度\(O(n^2)\)。

点击查看代码

#include<bits/stdc++.h>
#define N 3010
using namespace std;
int n,a[N],f[N][N];
signed main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) f[i][j]=1;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=i;j++){
			int k=i-j;
			if(k&&a[i]!=a[k]) continue;
			f[i][j]=max(f[i][j],f[k][j]+1);
		}
	}
	int ans=-514;
	for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) ans=max(ans,f[i][j]);
	cout<<ans<<"\n";
	return 0;
}

D - Santa Claus 2

对线段上的点容斥不好考虑，可以反过来依次考虑每个房子是否在一个线段上。

显然可以单独考虑行和列，用set分别维护 每一行中横向线段 与 每一列中竖向线段 的连通性，对于每个房子，依次在行和列上判断是否位于一个线段中即可。

时间复杂度\(O((n+m)\log^2 n)\)（其中一个\(log\)是map的，换用哈希表可以去掉）。

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define N 200010
#define M 200010
using namespace std;
struct House{int x,y;}a[N];
map<int,multiset<pair<int,int>>> hor,ver;
int n,m,sx,sy,num[256],ans;
void merge(map<int,multiset<pair<int,int>>>& ma){//求线段并
	for(auto &i:ma){
		auto &se=i.second;
		se.insert({LLONG_MIN,LLONG_MIN});
		for(auto j=++se.begin(),k=j;j!=se.end();j++){
			k=j,k--;
			if(k->second>=j->first){
				pair<int,int> tmp={k->first,max(k->second,j->second)};
				se.erase(j),se.erase(k);
				j=se.insert(tmp);
			}
		}
	}
}
bool solve(multiset<pair<int,int>>& se,int v){
	if(se.empty()) return 0;
	auto it=--se.upper_bound({v,LLONG_MAX});
	return it->second>=v;
}
signed main(){
	num['U']=0,num['R']=1,num['D']=2,num['L']=3;
	cin>>n>>m>>sx>>sy;
	for(int i=1;i<=n;i++) cin>>a[i].x>>a[i].y;
	for(int i=1,c;i<=m;i++){
		char d;
		cin>>d>>c;
		int xx=sx,yy=sy;
		if(num[1*d]&1){
			if(d=='L') sx-=c,hor[sy].insert({sx,xx});
			else sx+=c,hor[sy].insert({xx,sx});
		}else{
			if(d=='U') sy+=c,ver[sx].insert({yy,sy});
			else sy-=c,ver[sx].insert({sy,yy});
		}
	}
	merge(hor),merge(ver);
	for(int i=1;i<=n;i++)
		ans+=(solve(hor[a[i].y],a[i].x)||solve(ver[a[i].x],a[i].y));
	cout<<sx<<" "<<sy<<" "<<ans<<"\n";
	return 0;
}

用set代替multiset也是可以的，反正重复的线段就算作一条了。

E - Snowflake Tree

可以发现，确定中心点\(u\)以及\(x\)后，此时雪花树的顶点个数也就确定了，为\((\min\limits_{v} \deg(v))\times x+1\)，其中\(v\)是与\(u\)邻接的点。

我们要最大化上面这个式子。

因此我们可以枚举中心点，根据贪心的思想，我们将\(\deg(v)\)从大到小排序，对于确定的\(x\)，我们构建出的雪花树的第二层节点，就是排序后的前\(x\)个节点。

时间复杂度\(O(n\log n)\)。

点击查看代码

#include<bits/stdc++.h>
#define N 300010
#define int long long
using namespace std;
int n,deg[N],ans=LLONG_MIN;
vector<int> G[N],a;
signed main(){
	cin>>n;
	for(int i=1;i<n;i++){
		int u,v;
		cin>>u>>v;
		G[u].emplace_back(v),G[v].emplace_back(u);
		deg[u]++,deg[v]++;
	}
	for(int i=1;i<=n;i++){
		a.clear();
		for(int j:G[i]) a.emplace_back(deg[j]);
		sort(a.begin(),a.end(),[](int a,int b){return a>b;});
		int minn=LLONG_MAX,cnt=0;
		for(int j:a){
			minn=min(minn,j),cnt++;
			ans=max(ans,minn*cnt+1);
		}
	}
	cout<<n-ans<<"\n";
	return 0;
}

F - Visible Buildings

结论：将相邻的两个建筑顶部连直线，所有直线中截距的最大值与\(0\)取\(\max\)即为答案。

证明：（如果不相邻答案一定不优）

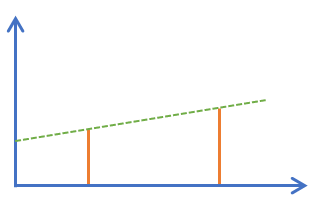
如下图，假设两个建筑之间还有一个建筑（黄色），则根据它与绿色直线的位置关系进行讨论：

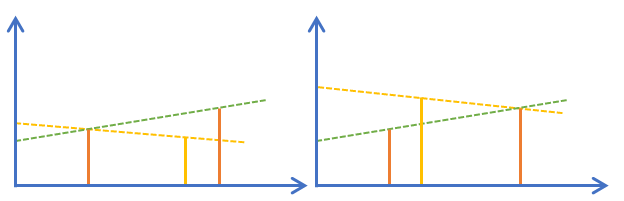
不难发现，无论它在绿色直线的上方还是下方，我们总能把它与相邻的建筑进行连线，使得新直线的截距更大。所以如果两建筑不相邻，考虑它们一定不会让答案更优。

时间复杂度\(O(n)\)。

注意：

• 所有截距都\(<0\)时需要输出\(-1\)，此时不能保留小数，否则会判错。
• 求截距需要用到除法，判断负数坐标可能有精度误差，应当直接考虑被除数与除数的关系，以直接判定商的正负性。
  经测试，直接使用除法不会出现问题。

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define double long double
#define N 300010
using namespace std;
int n,x[N],y[N];
signed main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>x[i]>>y[i];
	double ans=-1e18;
	for(int i=1;i<n;i++){
		double yy=-1.0*(y[i]*x[i+1]-x[i]*y[i+1])/(x[i]-x[i+1]);
		ans=max(ans,yy);
	}
	if(ans<0) cout<<"-1\n";
	else cout<<fixed<<setprecision(15)<<ans<<"\n";
	return 0;
}