第4章 李群李代数
一、概述
-
李群和李代数的核心思想
-
可以理解为专门用于矩阵旋转的东西,符合
封结幺逆法则; -
李群可以理解为
旋转矩阵,李代数可以理解为旋转向量; -
李群是连续群,李代数可以表出李群的导数,所以李代数表示的是李群的局部性质;
-
进而我们可以理解为:旋转向量表达了旋转矩阵的局部(旋转发生那一瞬间的领域内)性质;
-
由拉格朗日中值定理可知:导数控制函数。李代数控制李群,\(\phi\)控制\(R\);【1】
也就是说想要估计出函数值,我们可以研究该函数的导数,用来描述某个点领域内性质。故而我们需要建立对李群的求导模型,通过分析导数的性质来估计出相机在这一时刻(领域内)的位姿。
但是我们知道
群是指只有一个运算的集合(我们选择矩阵乘法),所以李群不对加法封闭【2】,但是我们知道李代数是建立在向量空间上的,支持加法运算。所以我们需要一种让李群映射到李代数的机制,然后通过对李代数求导,求出李群的导数。不过,对李代数求导后的结果非常复杂,所以我们需要寻找另外一种求导方式【3】,这就是我们接下来所要介绍的内容。【注】
【1】:某个名牌大学考研的复试题——你知道导数的作用是什么吗?
【2】:李群也是一种群。甭跟我扯什么鳄鱼不是鱼、日本人不是人。
【3】:对谁求导不重要,因为我们总可以通过这个导数控制相同的函数。
-
-
李群的两种求导模型(都是映射到了李代数空间)
-
BCH公式线性化(将李群的变化与李代数的变化联系起来);
-
对李代数求导的
求导模型;(复杂)- 需要求出左右雅可比矩阵的逆;
-
对微扰动求导的
扰动模型;(精简)- 不需要求出左右雅可比矩阵的逆;
-
-
这两种求导模型都是会有误差存在的
-
李群和李代数的基础符号
-
特殊正交群\(SO(3)\),特殊欧式群\(SE(3)\);
-
特殊正交群上的李代数\(\mathfrak{so}(3)\),这里我们具象化为三维\(\phi\)向量或者反对称阵\(\widehat{\phi}\);
![李代数so(3)的定义]()
-
特殊欧式群上的李代数\(\mathfrak{se}(3)\),这里我们具象化为六维\(\xi\)向量或者四维方阵\(\widehat{\xi}\);
![李代数se(3)的定义]()
\(\rho\)表示三维空间中的平移,\(\phi\)表示三维空间中的旋转。
-
反对称矩阵与相应的三维向量:\(\wedge\)和\(\vee\);
![反对称矩阵与相应的三维向量]()
-
向量\(\overrightarrow{a}\)和\(\overrightarrow{\omega}\)都表示旋转向量的单位方向向量,\(\theta\)表示旋转角,\(\overrightarrow{\phi}\)表示旋转向量,\(R\)表示旋转矩阵;
-
有时为了格式不显得过于复杂,会省略掉向量标识\(\overrightarrow{}\);
-
-
Sophus库的使用
-
\(SO(3)\)和\(\mathfrak{so}(3)\)
// 构造旋转向量、旋转矩阵、四元数 Eigen::AngleAxisd RV = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)); Eigen::Matrix3d RM = RV.toRotationMatrix(); Eigen::Quaterniond QD(RM); // 通过上述旋转表述构造李群 Sophus::SO3d SO3_RM(RM); Sophus::SO3d SO3_QD(QD); // 输出SO(3)时,以so(3)形式输出 cout << "SO(3) from matrix :" << SO3_RM.log().transpose() << endl; cout << "SO(3) from quaternion:" << SO3_QD.log().transpose() << endl; // 使用对数映射获得它的李代数 Eigen::Vector3d so3 = SO3_RM.log(); cout << "so3 = " << so3.transpose() << endl; // hat为向量到反对称矩阵 cout << "so3 hat=" << endl << Sophus::SO3d::hat(so3) << endl; // vee为反对称矩阵到向量 cout << "so3 hat vee= " << Sophus::SO3d::vee(Sophus::SO3d::hat(so3)).transpose() << endl; // 增量扰动模型的更新 Eigen::Vector3d update_so3(1e-4, 0, 0); Sophus::SO3d SO3_updated = Sophus::SO3d::exp(update_so3) * SO3_RM; cout << "SO3 updated = " << endl << SO3_updated.matrix() << endl; -
\(SE(3)\)和\(\mathfrak{se}(3)\)
// 构造旋转向量、旋转矩阵、四元数 Eigen::AngleAxisd RV = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)); Eigen::Matrix3d RM = RV.toRotationMatrix(); Eigen::Quaterniond QD(RM); // 通过上述旋转表述构造李群 Sophus::SO3d SO3_RM(RM); Sophus::SO3d SO3_QD(QD); // 对SE(3)操作大同小异 Eigen::Vector3d t(1,0,0); // 沿X轴平移1 Sophus::SE3d SE3_RMt(RM, t); // 从R,t构造SE(3) Sophus::SE3d SE3_QDt(QD, t); // 从q,t构造SE(3) cout << "SE3 from RM,t = " << SE3_RMt.log().transpose() << endl; cout << "SE3 from QD,t = " << SE3_QDt.log().transpose() << endl; // 李代数se(3) 是一个六维向量,方便起见先typedef一下 typedef Eigen::Matrix<double,6,1> Vector6d; Vector6d se3 = SE3_RMt.log(); cout << "se3 = " << se3.transpose() << endl; // 观察输出,会发现在Sophus中,se(3)的平移在前,旋转在后. // 同样的,有hat和vee两个算符 cout << "se3 hat = " << endl << Sophus::SE3d::hat(se3) << endl; cout << "se3 hat vee = " << Sophus::SE3d::vee(Sophus::SE3d::hat(se3)).transpose() << endl; // 最后,演示一下更新 Vector6d update_se3; //更新量 update_se3.setZero(); update_se3(0,0) = 1e-4; Sophus::SE3d SE3_updated = Sophus::SE3d::exp(update_se3) * SE3_RMt; cout << "SE3 updated = " << endl << SE3_updated.matrix() << endl;
-
二、详述
-
从物理角度引出
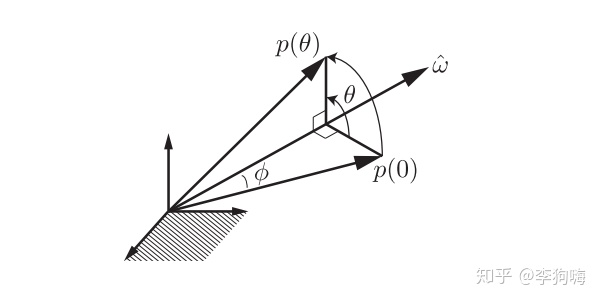
![从物理角度引出]()
假设有一个三维的向量\(\overrightarrow{p(0)}\)绕着旋转轴\(\overrightarrow{\omega}\)旋转了\(\theta\)角度(旋转所需时间为\(t\))到达了\(\overrightarrow{p(t)}\)处,由小学二年级就学过的知识知道:\(\overrightarrow{速度}=\overrightarrow{角速度}\times\overrightarrow{(旋转中心,旋转点)}\)。
我们不妨设\(\overrightarrow{p(t)}\)领域处的速度为\(\overset{\bullet}{\overrightarrow{p(t)}}\),故而有公式:\(\overset{\bullet}{\overrightarrow{p(t)}}=\overrightarrow{\omega}\times\overrightarrow{p(t)}=\widehat{\overrightarrow{\omega}}\cdot\overrightarrow{p(t)}\)【1】。这其实是一个关于\(\overrightarrow{p(t)}\)的微分方程【2】,并且当\(\overrightarrow{\omega}\)是单位向量,即值为\(1\ \mathbf{rad/s}\)时有\(\theta=t\),所以不难解出:
\[\overrightarrow{p(t)}=e^{\widehat{\overrightarrow{\omega}}\cdot{t}}\cdot{\overrightarrow{p(0)}},由此我们不难看出\overrightarrow{p(0)}到\overrightarrow{p(t)}的旋转矩阵:R(t)=e^{\widehat{\overrightarrow{\omega}}\cdot{t}}=e^{\widehat{\overrightarrow{\omega}}\cdot{\theta}}=e^{\widehat{\overrightarrow{\phi}}}; \]所以我们便可的出结论:旋转向量和旋转矩阵存在指数映射关系,且多对一对应(旋转周期性)。
为了统一化表述,我们称旋转矩阵为李群\(SO(3)\),旋转向量为\(\mathfrak{so}(3)\),它们之间有指数映射关系。
注【1】:如果这个时候你仍然以向量为参考,那可能有点儿不太好理解,但要是将视线移至坐标系身上的化,也就是说是坐标系在旋转,那就不难理解:旋转轴是\(\overrightarrow{\omega}\),旋转中心是原点。
注【2】:标量微分方程与矢量微分方程如下所示:
\[\begin{aligned} &\overset{\bullet}{x(t)}=a\cdot{x(t)},且x(0)=x_0&\Longrightarrow&\quad x(t)=e^{at}\cdot{x_0}; \\\\ &\overset{\bullet}{X(t)}=A\cdot{X(t)},且X(0)=X_0&\Longrightarrow&\quad X(t)=e^{At}\cdot{X_0}; \end{aligned} \] -
指数与对数映射
-
矩阵的泰勒展开
\[e^{\widehat{\overrightarrow{\omega}}\cdot{\theta}}=\sum_{n=0}^{\infty}{\frac{1}{n!}(\overrightarrow{\omega}}{\theta})^n=\sum_{n=0}^{\infty}{\frac{{\theta}^n}{n!}(\overrightarrow{\omega}})^n \] -
反对称阵的性质
\[\begin{cases} \widehat{\overrightarrow{\omega}}\cdot{\widehat{\overrightarrow{\omega}}}=\overrightarrow{\omega}\cdot{\overrightarrow{\omega}^T}-I \\\\ \widehat{\overrightarrow{\omega}}\cdot{\widehat{\overrightarrow{\omega}}\cdot{\widehat{\overrightarrow{\omega}}}}=-{\widehat{\overrightarrow{\omega}}} \end{cases} \] -
指数映射的推导
-
\(\mathfrak{so}(3) \Longrightarrow SO(3)\)的推导
![SO(3)的指数映射推导过程]()
-
\(\mathfrak{se}(3) \Longrightarrow SE(3)\)的推导
![SE(3)的指数映射推导过程]()
如果你尝试这将上面的\(J\)泰勒展开,将会得到下面的公式(请务必有印象!):
![SE(3)的指数映射推导过程2]()
而旋转矩阵\(R\)通过上述的\(\mathfrak{so}(3) \Longrightarrow SO(3)\)已经给出。
-
-
对数映射的推导
-
\(SO(3)\Longrightarrow\mathfrak{so}(3)\)的推导
![SO(3)的对数映射推导过程]()
只有伞兵才会这样推导,之前在《矩阵旋转》中就提到了如何从旋转矩阵到旋转向量,我们只需知道旋转矩阵的迹\(\mathbf{tr}(R)\)解出\(\theta\),并解出特征值为1的特征向量并归一化得到\(\omega\)。
-
\(SE(3)\Longrightarrow\mathfrak{se}(3)\)的推导
由上述\(SO(3)\Longrightarrow\mathfrak{so}(3)\)我们可以通过旋转\(R\)求出旋转向量\(\phi\),而\(\overrightarrow{t}=J\rho\)得\(\rho=J^{-1}\overrightarrow{t}\);
-
-
-
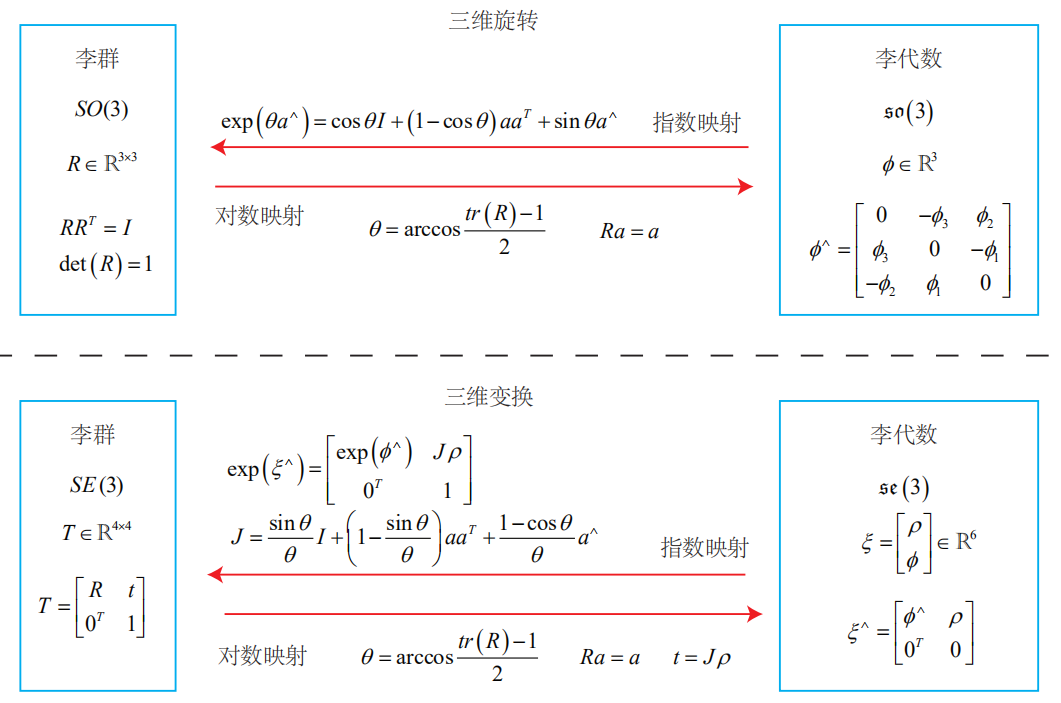
李群和李代数的对应关系
![李群和李代数的对应关系]()
三、李代数的求导和扰动模型(左乘)
-
BCH公式和它的线性近似式
-
BCH公式的引出
在高等数学中,我们研究的大部分问题都是标量(也就是纯数值)的问题,所以一定满足下面恒等式
\[\ln(e^A\cdot{e^B})\equiv{A+B}\\ \ln(e^\widehat{a}\cdot{e^\widehat{b}})\equiv{(a+b)^{\wedge}} \]但是很不幸的是,我们在SLAM中研究的是向量(或者说矩阵),反正不是标量,所以不能满足上式。这个东西在向量空间中的计算很是复杂,但是这个世界上总有些神仙捣鼓这种玩意儿,比如Baker-Campbell-Hausdorff这哥仨就为这个东西的计算给出了BCH公式。
-
BCH的完全展开
\[\ln(e^A\cdot{e^B})=A+B+\frac{1}{2}[A,B]+\frac{1}{12}[A,[A,B]]-\frac{1}{12}[B,[A,B]]+\cdots \]其中\([,]\)表示李括号运算。也就是说,这天底下就没有干干净净的事,矩阵指数之积会产生一堆李括号余项。
-
BCH线性近似式
但凡事不能说得太绝对。虽说这BCH公式的完全展开很复杂,但是后面那一堆东西叫做余项啊!也就是说,当\(\overrightarrow{\phi_1}\)或者\(\overrightarrow{\phi_2}\)是小量的时候,它们的高阶就是高阶无穷小量了,可以被忽略的!这个时候BCH公式就变得非常‘和蔼可亲’了(近乎线性的表达)
\[\ln(e^{\widehat{\phi_1}}\cdot{e^{\widehat{\phi_2}}})^{\vee}\approx \begin{cases} 左乘模型:J_l^{-1}(\phi_2)\cdot{\phi_1}+\phi_2,当\phi_1为小量时; \\\\ 右乘模型:J_r^{-1}(\phi_1)\cdot{\phi_2}+\phi_1,当\phi_2为小量时; \end{cases} \]至此,我们将李群\(SO(3)\)(旋转矩阵)和李代数\(\mathfrak{so}(3)\)(旋转向量)线性化了。
可以理解为:旋转矩阵\(R_2\)左乘了一个微小旋转矩阵\(R_1\),相当于旋转向量\(\phi_2\)加上了经过左雅可比逆\(J_l^{-1}(\phi_2)\)旋转后的旋转向量\(\phi_1\)。右乘微小矩阵\(R_2\)亦可模仿理解。
-
BCH公式的意义
-
李群 \(\Longrightarrow\) 李代数
\[\begin{cases} 左乘模型:e^{\widehat{\Delta\phi}}\cdot{e^{\widehat{\phi}}}=e^{【J_l^{-1}(\phi)\cdot{\Delta\phi}+\phi】^{\wedge}} \\\\ 右乘模型:e^{\widehat{\phi}}\cdot{e^{\widehat{\Delta\phi}}}=e^{【J_r^{-1}(\phi)\cdot{\Delta\phi}+\phi】^{\wedge}} \end{cases} \] -
李代数 \(\Longrightarrow\) 李群
\[e^{【\phi+\Delta\phi】^{\wedge}}= \begin{cases} 左乘模型:e^{【\phi+J_l^{-1}(\phi)\cdot{J_l(\phi){\Delta\phi}}】^{\wedge}} =e^{【J_l(\phi){\Delta\phi}】^{\wedge}}\cdot{e^{\widehat{\phi}}} \\\\ 右乘模型:e^{【\phi+J_r^{-1}(\phi)\cdot{J_r(\phi){\Delta\phi}}】^{\wedge}} =e^{\widehat{\phi}}\cdot{e^{【J_r(\phi){\Delta\phi}】^{\wedge}}} \end{cases} \] -
李代数解决李群的求导问题
李群没有加法,所以很难用导数的一般定义去求导数,但是李代数允许加法【1】。所以如果想要对李群求导数,我们可以运用指数映射法则和BCH公式转换成李代数,然后用定义区求导数(乘除变加减)。
【注】【1】:李群是群,不对加法封闭。李代数定义在向量空间,对加法封闭。
-
-
左右雅可比矩阵的计算
![左右雅可比矩阵的计算]()
-
在\(SE(3)\)上同样有线性化公式
![在SE(3)上同样有线性化公式]()
其中的左右雅可比矩阵表述十分复杂,并且我们以后不会用到它来计算,所以就将其视为一个常数符号。
-
-
李代数\(SO(3)\)的求导
假设一个向量\(\overrightarrow{p}\)经过了旋转矩阵\(R\)的作用,旋转矩阵对应的李代数(旋转向量)为\(\phi\);
-
对李代数求导(求导模型)
\[公式 控制\begin{aligned} &\frac{\part{(Rp)}}{\part{\phi}} = \frac{\part{(Rp)}}{\part{\phi}} = \frac{\part{(e^{\widehat{\phi}}\cdot{p})}}{\part{\phi}} \\\\=&\underset{\Delta\phi\rightarrow0}{\lim} \frac{(e^{(\phi+\Delta\phi)^{\wedge}}-e^{\phi^{\wedge}})\cdot{p}}{\Delta\phi} ,(利用左乘模型得) \\\\=&\underset{\Delta\phi\rightarrow0}{\lim} \frac{(e^{【J_l(\phi){\Delta\phi}】^{\wedge}}\cdot{e^{\widehat{\phi}}}-e^{\phi^{\wedge}})\cdot{p}}{\Delta\phi} ,(利用矩阵的等价无穷小替换) \\\\=&\underset{\Delta\phi\rightarrow0}{\lim} \frac{【J_l(\phi){\Delta\phi}】^{\wedge}\cdot{e^{\widehat{\phi}}p}}{\Delta\phi} ,(将反对陈矩阵\wedge符号换成叉积\times,再交换顺序) \\\\=& -【e^{\widehat{\phi}}p】^{\wedge}J_l(\phi) = -(Rp)^{\wedge}J_l{(\phi)} \end{aligned} \] -
对微扰动求导(扰动模型)
假设这个时候对\(R\)有一个作用在左边的微小扰动\(\Delta R\),对应的李代数为\(\psi\)。(左右干扰模型不同!!)
\[\begin{aligned} &\frac{\part{(Rp)}}{\part{\psi}} = \frac{\part{(Rp)}}{\part{\psi}} = \frac{\part{(e^{\widehat{\phi}}\cdot{p})}}{\part{\psi}} \\\\=&\underset{\Delta\phi\rightarrow0}{\lim} \frac{(e^{\psi^{\wedge}}e^{\phi^{\wedge}}-e^{\phi^{\wedge}})\cdot{p}}{\psi} ,(利用矩阵的等价无穷小替换) \\\\=&\underset{\Delta\phi\rightarrow0}{\lim} \frac{\psi^{\wedge}\cdot{e^{\phi^{\wedge}}p}}{\psi} ,(将反对陈矩阵\wedge符号换成叉积\times,再交换顺序) \\\\=& -【e^{\widehat{\phi}}p】^{\wedge}=-(Rp)^{\wedge} \end{aligned} \]
-
-
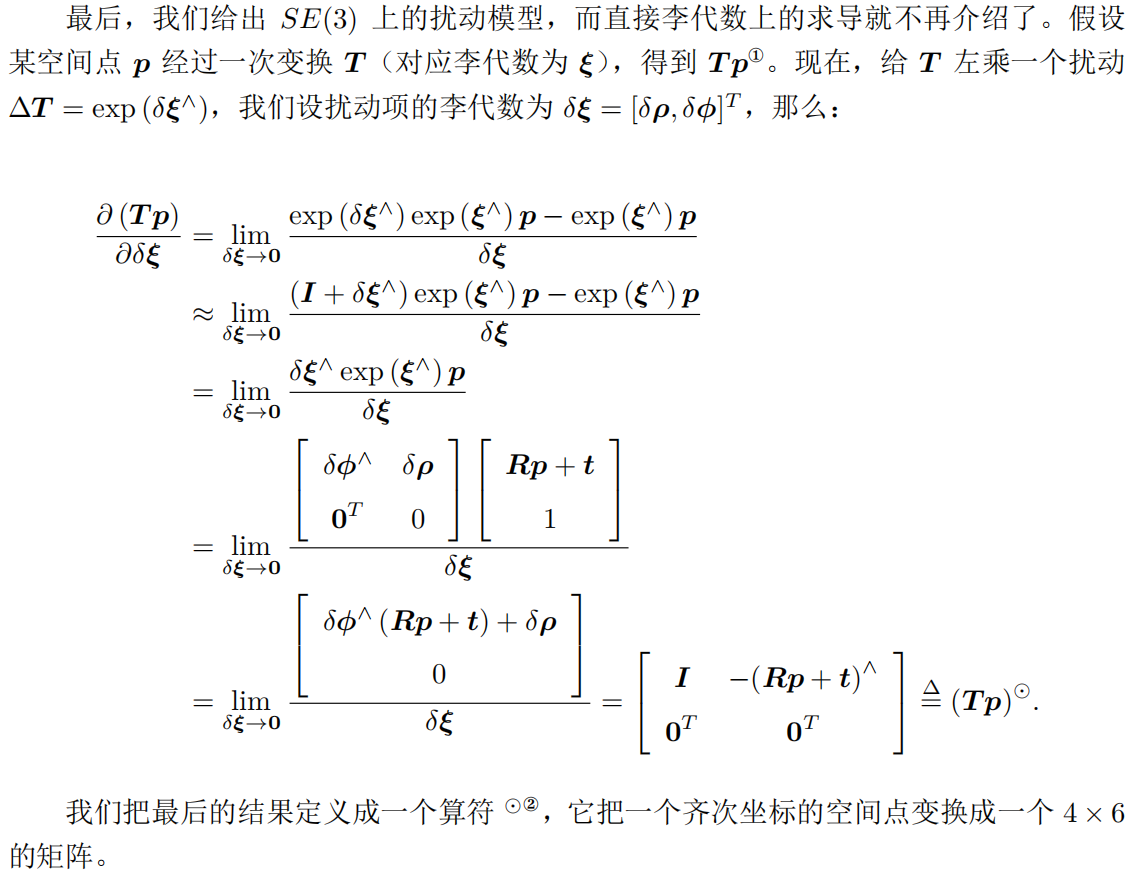
李代数\(SE(3)\)的求导
![李代数SE(3)的求导]()
第2、3行是因为用矩阵的等价无穷小替换;
四、评估轨迹的误差
-
向量的长度(或大小)
-
欧式距离
在三维及三维以下的向量空间中,向量的长度的平方是坐标值的平方和。
-
欧式推广
在n维坐标系中,我们也可以用这一思想表示向量的长度(或者称之为大小)。
\[\overrightarrow{\alpha}=[\alpha_1,\alpha_2,\cdots,\alpha_n]^T,则||\overrightarrow{\alpha}||_2^2=\alpha_1^2+\alpha_2^2+\cdots+\alpha_n^2 \]
-
-
矩阵的左右乘法区别
-
每个位姿李代数误差
我们记第\(i\)时刻的真实轨迹为\(T_{(GT,i)}\)、观测(估计)轨迹为\(T_{(Esti,i)}\)、绝对轨迹误差\(T_{(ATE,i)}\)。
由于误差的作用使得真实轨迹变换到了估计轨迹,我们的关注点是坐标系的变换,所以有三者的转换公式:\(T_{(Esti,i)}=T_{(GT,i)}\cdot{T_{(ATE,i)}}\),即有\(T_{(ATE,i)}=T_{(GT,i)}^{-1}\cdot{T_{(Esti,i)}}\)。
得到了每个位姿的误差公式,那如何确定误差的大小呢?我们知道李群是很难估计大小的,所以我们可以借助其对应的李代数来确定大小,这就需要用到对数映射公式:\(\xi=【\log(T)】^{\vee}\)。
所以每个位姿的李代数上的误差为:\(【\log(T_{(GT,i)}^{-1}\cdot{T_{(Esti,i)}})】^{\vee}\),那么它的大小也就可以用二范数来计算。
当然我们也可以计算第i时刻的邻域\(\Delta{t}\)时间内,真实轨迹(的变化量)与估计轨迹(的变化量)的相对误差:
\[【\log(T_{(GT,i)}^{-1}\cdot{T_{(GT,i+\Delta{t})}})^{-1}(T_{(Esti,i)}^{-1}\cdot{T_{(Esti,i+\Delta{t})}})】^{\vee} \]


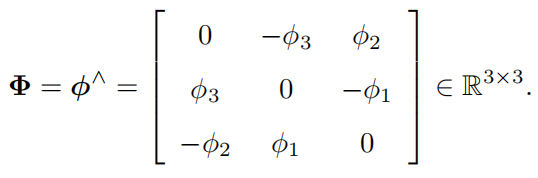
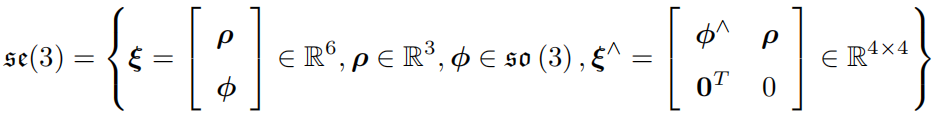
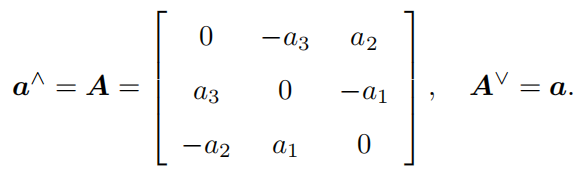
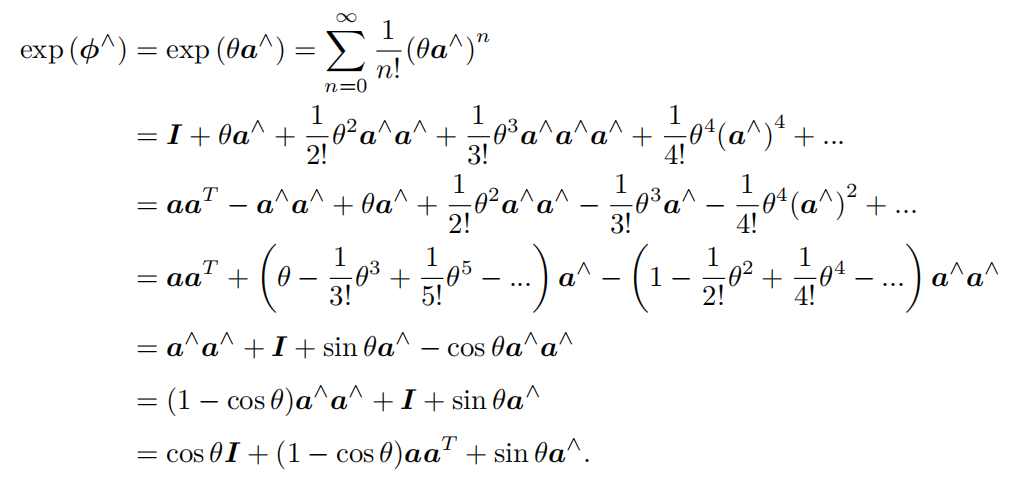
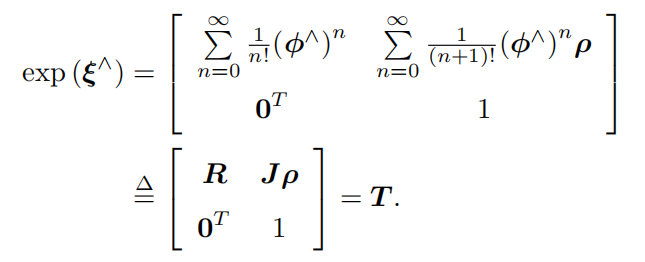
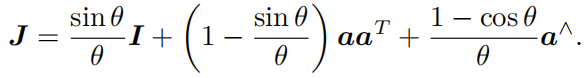
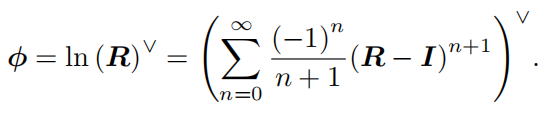

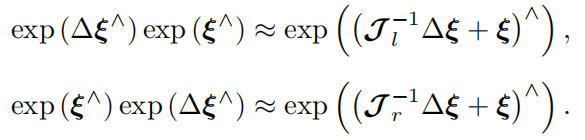

 浙公网安备 33010602011771号
浙公网安备 33010602011771号