摘要:
第1章 线性空间与线性映射 求解过渡矩阵(表示矩阵)并进行坐标变换; 空间Vn(F):ξ=[ξ1⋯ξn]和η=[η1⋯ηn]是基,T是线性变换,α∈Vn(F)任意。 已知α在ξ下的坐标为x=[x1⋮xn],ξ→η的过度矩阵为C,则α在η下的坐标为y=C−1x; 已知T在ξ下的表示矩阵为A,ξ→η的过 阅读全文
posted @ 2022-11-06 21:47
BNTU
阅读(829)
评论(0)
推荐(0)
 一、概述 李群和李代数的核心思想 可以理解为专门用于矩阵旋转的东西,符合封结幺逆法则; 李群可以理解为旋转矩阵,李代数可以理解为旋转向量; 李群是连续群,李代数可以表出李群的导数,所以李代数表示的是李群的局部性质; 进而我们可以理解为:旋转向量表达了旋转矩阵的局部(旋转发生那一瞬间的领域内)性质; 阅读全文
一、概述 李群和李代数的核心思想 可以理解为专门用于矩阵旋转的东西,符合封结幺逆法则; 李群可以理解为旋转矩阵,李代数可以理解为旋转向量; 李群是连续群,李代数可以表出李群的导数,所以李代数表示的是李群的局部性质; 进而我们可以理解为:旋转向量表达了旋转矩阵的局部(旋转发生那一瞬间的领域内)性质; 阅读全文
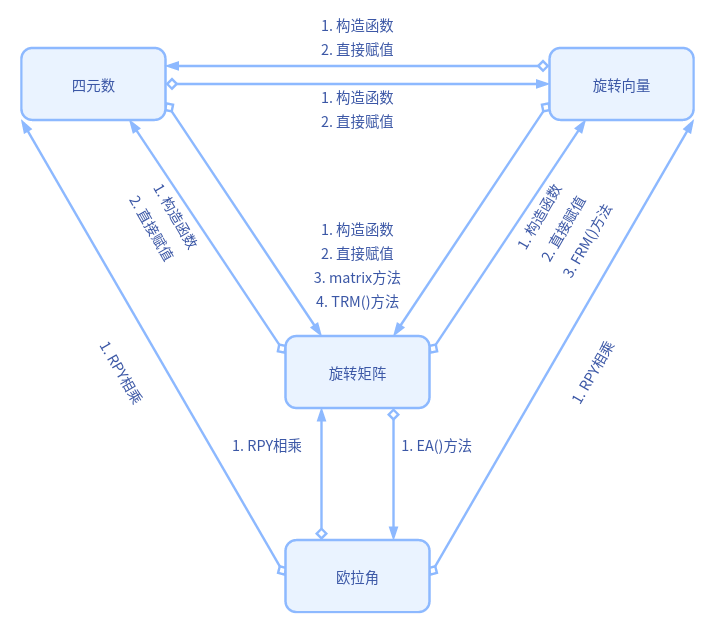 一、概述 旋转变换的核心思想 在不同坐标系下,虽然坐标不同,但是同一个向量还是一样的。这句话有点儿怪怪的,但是可以用数学公式表出:\(\beta_1^T\cdot\alpha_1=\beta_2^T\cdot\alpha_2\),其中\(\beta\)是不同坐标系的标准正交基(行分块),\(\alp 阅读全文
一、概述 旋转变换的核心思想 在不同坐标系下,虽然坐标不同,但是同一个向量还是一样的。这句话有点儿怪怪的,但是可以用数学公式表出:\(\beta_1^T\cdot\alpha_1=\beta_2^T\cdot\alpha_2\),其中\(\beta\)是不同坐标系的标准正交基(行分块),\(\alp 阅读全文