基础篇_005_运算符

　　在Python中一共有5种运算符：算数运算符、赋值运算符、关系运算符、成员运算符、逻辑运算符和位运算符。

----算数运算符 ===》最简单的运算符，没有之一：

　　1. 加（+）、减（-）、乘（*）、除（/） 　　===》这是简单的四则运算。

　　2. 求指数幂：** 　　　　　　　　　　　　　===》eg：2 ** 2 = 4。

　　3. 求模（余数）和商：分别是 % 和 // 　　　===》eg：9 % 2 = 1；9 // 2 = 4。

这里有一点需要注意：如果除数是负数，那么余数必然是负数。

证明：由其性质：| 余数 - 除数 | < | 除数 | （这个...我也不会证明，网上搜也没能搜到）可分为4中情况 《===》

　　1. 余数 - 除数 > 0 && 除数 > 0 ===》  余数 - 除数 <   除数，三式联解得：余数 >     0　　&& 除数 > 0 && 除数 > 余数

　　2. 余数 - 除数 > 0 && 除数 < 0 ===》  余数 - 除数 < - 除数，三式联解得：余数 > 2 * 除数 && 除数 < 0 && 除数 > 余数

　　3. 余数 - 除数 < 0 && 除数 > 0 ===》- 余数 + 除数 <   除数，三式联解得：余数 < 2 * 除数 && 除数 > 0 && 除数 < 余数

　　4. 余数 - 除数 < 0 && 除数 < 0 ===》- 余数 - 除数 < - 除数，三式联解得：余数 < 　　0 　 && 除数 < 0 && 除数 < 余数

 

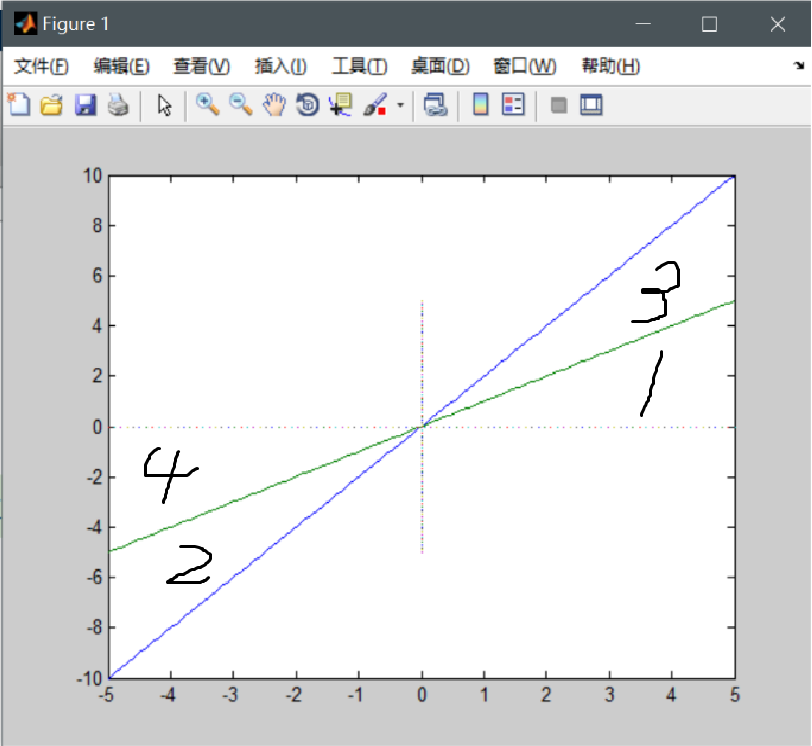
　　由图可见：余数和除数必然同号！

　　当然这种方法有些笨拙不好理解，那么大家现在可以想象一下：假设有两个整数m和n，要求满足 | m - n | < | m |，那利用反证法，如果m与n不同号，由于负数减去一个正数会负得更多（或者正数减去一个负数会正得更多），这样造成与条件矛盾 ===》余数和除数必然同号。

 

----赋值运算符 ===》优先级最低的运算符

　　1. 单纯的“=”：直接赋值。

　　2. “算术运算符”与“=”相连：将变量经相应的算术运算后重新赋值给该变量。

 

----关系运算符 ===》其值为布尔类型

　　1. 大于（>）、小于（>）、大于等于（≥）、小于等于（≤）

　　2. 判断是否等于：等于（==）、不等于（!=）

 

----成员运算符：in和not in ===》其值也是布尔类型，用于判断字符串中是否含有相应的子序列（子字符串）。eg：

if "Simba" in "Simba是大帅哥":
　　print("Yes")

 

----逻辑运算符 ===》其值也为布尔类型

　　1. and：逻辑与；相当于&&

　　2. or ：逻辑或；相当于||

　　3. not：逻辑非；相当于 !

在逻辑运算中，Python有这样一套规定：not的优先级最大，相当于是和表达式的值黏在一起的，and和or拥有相等的优先级，当遇到一长串逻辑运算表达式的时候，Python会从左到右依次运算 ===》

　　1. 当碰到and的时候，如果前面的值为True， 则继续执行；如果前面的值为False，则整个表达式的值为False。

　　2. 当碰到or 的时候，如果前面的值为False，则继续执行；如果前面的值为True， 则整个表达式的值为True 。

 

----位运算符 ===》这个有利于深层次的理解计算机的一些运算

　　1.  “按位与”运算 ：& 。　　对应都是1的时候结果才是1，否则为0；　　 结果的精度与精度高的操作数的精度相同。

　　2.  “按位或”运算 ：| 。　　对应都是0的时候结果才是0，否则为1；　　 结果的精度与精度高的操作数的精度相同。

　　3. “按位异或”运算：^ 。对应都是0或者都是1的时候结果才是0，否则为1；结果的精度与精度高的操作数的精度相同。

　　4. “按位取反”运算：~ 。对应位上0和1互换。

　　5.  “左移位”运算 ：<<。高端溢出位被丢弃，低位补上0 ===》左移n位相当于乘上2的n次幂。

　　6.  “右移位”运算 ：>>。先将低位丢弃，如果高端位是1（表示该数为负数），则在左端补上1；如果高端位是0（表示该数为正数），则在左端补上0；

扩展：在计算机内存中如何表示负数？ ===》负数可以将最高位置为1，但是这样不利于运算，所以一般采用补码来表示：

——当原码是正数时，反码和补码就是原码；

——当原码是负数时，反码就是原码的符号位不变，其余位“按位取反”，补码 = 反码 + 1 （加上1是为了保证+0和-0的二进制码一样）

 

----老问题：运算符的优先级 ===》https://www.cnblogs.com/pangdajin/p/8680265.html

总的来说就是：

　　1. 最高：单目运算符（() > 取相反数）

　　2. 次之：双目运算符（算数运算符 > 移位运算符 > 关系运算符 > 按位逻辑运算符 > 逻辑运算符）

　　3. 较低：三目运算符（条件——condition ？command1 ：command2 ）

　　4. 最低：赋值运算符