动态运动基元与二阶线性系统

前言

动态运动基元(Dynamic Movement Primitive, DMP)，是一种轨迹规划的模仿学习方法，其在学术界有大量的相关论文研究，但是至今未有教材完整的介绍 DMP 这一方法。本系列希望能够将 DMP 基础以更加通俗易懂的形式讲解 DMP，加入一些自己的理解，讲解一些 DMP 的初学者会困惑，论文和网上博客未曾讲到的东西。

ok，首先要回答一个问题，什么是动态运动基元 (Dynamic Movement Primitive, DMP)，首先来看一下 Ijspeert 教授在 2013 年动态运动基元开篇之作^[1]中写道的。

In this letter, we propose a generic modeling approach to generate multidimensional systems of weakly nonlinear differential equations to capture an observed behavior in an attractor landscape. The essence of our methodology is to transform well-understood simple attractor systems with the help of a learnable forcing function term into a desired attractor system. Both point attractor and limit cycle attractors of almost arbitrary complexity can be achieved.

在这篇 letter 中，我们提出了一种通用建模方法，用于生成多维弱非线性微分方程系统，以捕捉在吸引子（attrctor）景观中观察到的行为。我们方法的核心在于借助一个可学习的 forcing term 函数项，将已被充分理解的简单吸引子系统转换为目标吸引子系统。几乎任意复杂程度的点吸引子和极限环吸引子均可通过此方法实现。

至于在 DMP 一篇 IJRR 综述论文^[2]中，这样写道：

Dynamic Movement Primitives (DMPs) have their roots in the motor control of biological systems and can be seen as a rigorous mathematical formulation of the motion primitives as stable nonlinear dynamical systems (Schaal, 2006 a, 2006 b). In this respect, DMPs represent one of the first attempts to answer the research question:

动态运动基元起源于生物系统运动控制，可以看做是运动基元作为稳定的非线性动态系统的严格描述。在这方面年，DMP 是回答研究问题的首批尝试之一：

至于网上，其他 DMP 相关博客文章，无非是重复上述定义，我当时学 DMP 的时候一脸懵逼，虽然直到这是二阶线性系统的变体，所谓 \(\alpha _z\) , \(\beta _z\) 就类似于 PD 控制器中的 \(k_v\) , \(k_p\) 相关参数。尽管如此，但我仍然不知道这个运动基元所谓何物，以及动态运动基元到底是指这一条轨迹还是什么的。直到我后来翻看华中科技大学的机器人学课本关于二阶线性系统控制器的分解的讲解，才彻底理解。

二阶线性系统

下面讨论质量-弹簧-阻尼系统，图中受控对象处于零位。假设摩擦阻力与运动速度成正比，且无其他外力作用的情况下，物体自由运动的微分方程是

\[m\ddot{x}+b\dot{x}+kx=0 \]

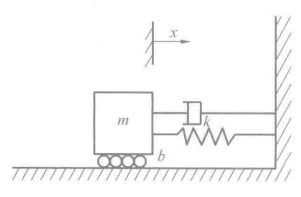
其对应特征方程为

\[ms^2+bs+k=0 \]

特征方程的根（系统的极点）是

\[s_1=-\frac{b}{2m}+\frac{\sqrt{b^2-4mk}}{2m},\ s_2=-\frac{b}{2m}-\frac{\sqrt{b^2-4mk}}{2m} \]

系统极点与系统运动状态和系统的动态性能，分为以下三种情况：

1. 方程有两个不等实根，即 \(b^2>4mk\)，系统过阻尼，阻尼占主导地位系统响应迟钝。
2. 方程有两复根，即 \(b^2<4mk\)，系统欠阻尼，刚度占主导地位，系统会产生振荡。
3. 方程有两相等复根，即 \(b^2=4mk\)，阻尼与刚度平衡，系统处于临界阻尼状态，可以产生尽可能快的非振荡反应。（此时，即对应 DMP 中经常提到的 \(\beta _z=4\alpha _z\) 的临界条件。DMP 可以理解为 m=1 的单位质量二阶线性系统）

上述是无外力作用下的系统响应过程，如果我们想让系统按照我们所期望的响应，或者说我们想要系统拥有一定的抗干扰能力。于是我们考虑对受控系统施加力 \(f\) 的作用。这里我们称之为驱动器。

于是物体的运动方程有

\[m\ddot{x}+b\dot{x}+kx=f \]

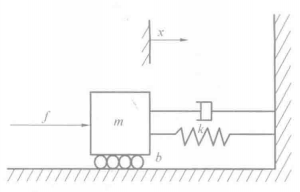
二阶线性系统推导 DMP 公式

下面我们来推导如何将普通的二阶线性系统（质量-弹簧-阻尼系统）转换成 DMP 这种弱二阶线性系统。

首先无外力作用下，有二阶线性系统

\[m\ddot{x}+b\dot{x}+kx=0 \]

其中，令 \(m=1, b=\alpha _z,\ k=\alpha _z\beta _z\) ，代入 \(b^2=4mk\) ，推得，\(\alpha _z=4\beta _z\) ，满足^[1:1][2:1]中临界条件。

\[\ddot{y}+\alpha _z\dot{y}+\alpha _z\beta _zy=0 \]

引入驱动器 \(f\)，对应 DMP 中的非线性力项（forcing term）。

\[\ddot{y}+\alpha _z\dot{y}+\alpha _z\beta _zy=f \]

令 \(y=y-g\)，这一变量替换是为了让系统的零位不在是 0 点，而是任意目标点（g）。于是有

\[\ddot{y}+\alpha _z\dot{y}+\alpha _z\beta _z\left( y-g \right) =f \]

移项合并同项，将 \(\ddot{y}\) 单独拿出来，于是有

\[\ddot{y}=\alpha _z\left( \beta _z\left( g-y \right) -\dot{y} \right) +f \]

增加对速度和加速度增加时间缩放项。这一系数加入是为了轨迹的时间泛化，控制轨迹的速度。具体介绍可以参考往期文章动态运动基元（DMP）时间放缩系数详解。

\[\tau ^2\ddot{y}=\alpha _z\left( \beta _z\left( g-y \right) -\tau \dot{y} \right) +f \]

写成一阶形式

\[\tau \dot{z}=\alpha _z\left( \beta _z\left( g-y \right) -z \right) +f \]

\[\tau \dot{y}=z \]

引入相位函数 \(x(t)\) 去除 DMP 去时间的显式依赖。上述方程中变量都是关于时间 \(t\) 的导数，\(f\) 也是关于时间 \(t\) 的函数，然而实际描述运动状态，或者描述轨迹的演化过程。习惯于说演化的开始与演化的结束。因此，我们这里使用一阶线性动力学引入时间的替代物^[1:2]。

\[\tau \dot{x}=-\alpha _xx \]

其中，\(\alpha _x\) 是一个常数。\(x=1\) 对应 \(t=0\)，表示演化的开始；\(x=0\) 对应 \(t=\infty\)，表示演化的结束，系统到达目标 g。

于是我们得到了 DMP 核心公式，整理如下：

\[\tau \dot{z}=\alpha _z\left( \beta _z\left( g-y \right) -z \right) +f\left( x \right) \]

\[\tau \dot{y}=z \]

注意这里是对相位函数 \(x\) 的导数。

---

1. Ijspeert A J, Nakanishi J, Hoffmann H, et al. Dynamical movement primitives: learning attractor models for motor behaviors[J]. Neural computation, 2013, 25(2): 328-373. ↩︎ ↩︎ ↩︎

2. Saveriano M, Abu-Dakka F J, Kramberger A, et al. Dynamic movement primitives in robotics: A tutorial survey[J]. The International Journal of Robotics Research, 2023, 42(13): 1133-1184. ↩︎ ↩︎