【笔记】欧拉图
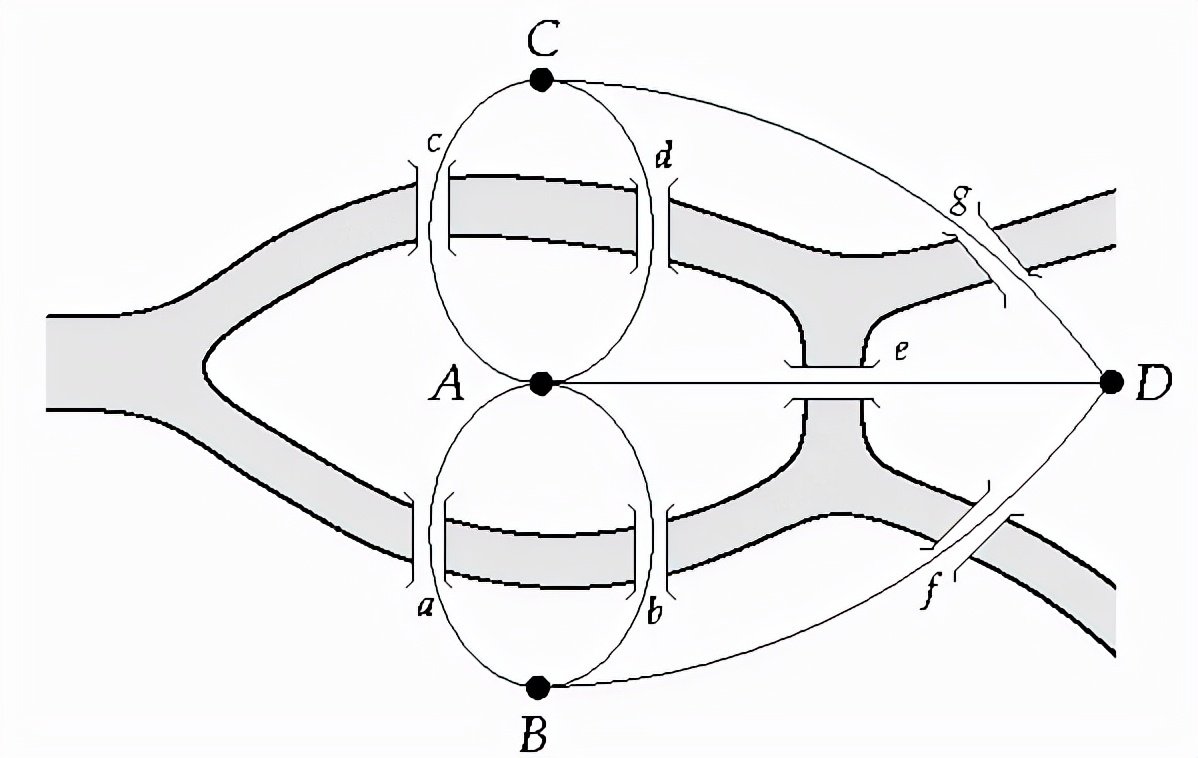
以上是图论经典问题:科尼斯堡七桥问题,由欧拉于 1736 年提出,旨在探讨图上的一笔画问题。
欧拉路径、欧拉回路
欧拉路径:图中经过所有边恰好一次的路径(即一笔画)。若该路径的起点与终点相同,则称其为一条欧拉回路。
判断
判断一个连通图是否存在欧拉路径:
有向图欧拉路径:图中恰存在 \(1\) 点,使其出度比入度多 \(1\)(作为起点 \(S\)),且恰存在 \(1\) 点,入度比出度多 \(1\)(作为终点 \(T\)),其余节点入度 \(=\) 出度。
有向图欧拉回路:所有点的入度 \(=\) 出度。此时 \(S\) 和 \(T\) 可为任意点。
无向图欧拉路径:图中恰存在 \(2\) 点度为奇数,其余点度均为偶数,则两度为奇数点可作为 \(S\) 和 \(T\)。
无向图欧拉回路:所有点度均为偶数。\(S\) 和 \(T\) 可为任意点。
存在欧拉回路时,一定存在欧拉路径。
存在欧拉回路的图叫欧拉图,仅存在欧拉路径的图叫半欧拉图。
证明不在此给出。
Luogu P1636 Einstein学画画
根据欧拉路径的判断,两奇点 \(+\) 若干偶点可以组成一条欧拉路径。因为题目没有规定一边只能画一次,所以同一个连通块内,奇点两两间都可以连成一条欧拉路径,只需要将奇点个数 \(\div 2\) 便可得到该连通块需要几笔画完。但要特判连通块上均为偶点的情况,此时可一笔画完。最后把所有连通块答案累加。
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
const int M=1e5+10;
int n,m,cnt,ans;
int deg[N];
int h[N],tot;
bool vis[N];
struct Node{
int to,nxt;
}e[2*M];
void Add(int u,int v){
tot++;
e[tot].to=v;
e[tot].nxt=h[u];
h[u]=tot;
}
void dfs(int u){
if(deg[u]&1) cnt++;
vis[u]=1;
for(int i=h[u];i;i=e[i].nxt){
int v=e[i].to;
if(vis[v]) continue;
dfs(v);
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
deg[u]++,deg[v]++;
Add(u,v),Add(v,u);
}
for(int i=1;i<=n;i++){
if(!vis[i]){
cnt=0;
dfs(i);
if(!deg[i]) continue;
if(cnt) ans+=cnt/2;
else ans++;
}
}
cout<<ans;
return 0;
}
UVA10129 单词 Play on Words
对于一个字符串,相当于一条连接首位字符的有向边。
首先需要判连通性,将有向边视为无向边,用并查集判断弱连通性。
然后按有向图欧拉路径存在条件判断,记录入度出度。
#include<bits/stdc++.h>
using namespace std;
const int N=50;
int T,n;
int ind[N],outd[N];
int fa[N];
int Find(int x){
if(fa[x]==x) return x;
else return fa[x]=Find(fa[x]);
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>T;
while(T--){
cin>>n;
memset(ind,0,sizeof(ind));
memset(outd,0,sizeof(outd));
for(int i=0;i<26;i++) fa[i]=i;
for(int i=1;i<=n;i++){
string s;
cin>>s;
int l=s[0]-'a',r=s[s.size()-1]-'a';
ind[r]++,outd[l]++;
l=Find(l),r=Find(r);
if(l!=r) fa[l]=r;
}
bool flag=0;
int p=-1;
for(int i=0;i<26;i++){
if(!ind[i]&&!outd[i]) continue;
if(Find(i)!=p&&(p!=-1)){
flag=1;
break;
}
p=fa[i];
}
if(flag){
cout<<"The door cannot be opened.\n";
continue;
}
int cnts=0,cnte=0;
for(int i=0;i<26;i++){
if(ind[i]==outd[i]) continue;
if(outd[i]-ind[i]==1) cnts++;
else if(ind[i]-outd[i]==1) cnte++;
else{
flag=1;
break;
}
}
if(!flag&&((!cnts&&!cnte)||(cnts==1&&cnte==1))) cout<<"Ordering is possible.\n";
else cout<<"The door cannot be opened.\n";
}
return 0;
}
Luogu P1333 瑞瑞的木棍
无向图版本。只需为字符串开一个 map,其余相同。
注意边数最大 \(2\times 10^5\),因此点数最大 \(5\times 10^5\)。
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
int T,n;
int d[N];
int fa[N],tot;
map<string,int> stk;
int Find(int x){
if(fa[x]==x) return x;
else return fa[x]=Find(fa[x]);
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
for(int i=1;i<=N-10;i++) fa[i]=i;
string s,t;
while(cin>>s>>t){
int l,r;
if(!stk[s]) stk[s]=++tot;
if(!stk[t]) stk[t]=++tot;
l=stk[s],r=stk[t];
d[l]++,d[r]++;
l=Find(l),r=Find(r);
if(l!=r) fa[l]=r;
}
bool flag=0;
int p=-1;
for(int i=1;i<=tot;i++){
if(Find(i)!=p&&(p!=-1)){
flag=1;
break;
}
p=fa[i];
}
if(flag){
cout<<"Impossible";
return 0;
}
int cnt=0;
for(int i=1;i<=tot;i++){
if(d[i]%2) cnt++;
}
if((!cnt)||(cnt==2)) cout<<"Possible";
else cout<<"Impossible";
return 0;
}
寻找
寻找一条欧拉路径:
- 确定起点 \(S\)。
- 从 \(S\) 开始 DFS。
DFS 伪代码:
void dfs(int u){
枚举 u 的出边
若该边未访问
标记为已访问
dfs(边指向的另一个点)
u 入栈
}
最后倒序输出栈内所有节点。
倒序输出的正确性:
- 若是欧拉回路,则欧拉路径不唯一,在遍历过程中,走到哪个点,哪个点就可以接在已走过的点后面,直到所有边都被走过,最终路径一定合法。
- 若是欧拉路径,则会遇到所有出边都被标记过而无路可走的情况。第一个遇到这种情况的一定会是欧拉路径终点,剩下的点都不会被走到而入栈,所以倒序输出仍然合法。
Luogu P7771【模板】欧拉路径
一个点可以被重复搜索,但边不能。
所以我们可以用一个数组 \(\Delta u\) 记录上次访问到的 \(u\) 的出边号,在向下搜索时,不会重复访问出边。
由于要求要按最小字典序输出,所以要对出边从小到大排序,因此使用 vector 存储。
#include<iostream>
#include<vector>
#include<algorithm>
#include<cstdio>
using namespace std;
const int maxn=1e5+10;
int n,m,s=1;
int ind[maxn],outd[maxn],r[maxn],cnt,d[maxn];
vector<int>g[maxn];
void dfs(int u){
for(int i=d[u];i<g[u].size();i=d[u]){
d[u]=i+1;
dfs(g[u][i]);
}
r[++cnt]=u;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
g[u].push_back(v);
outd[u]++,ind[v]++;
}
for(int i=1;i<=n;i++) sort(g[i].begin(),g[i].end());
int flag=0,cnt1,cnt2;
for(int i=1;i<=n;i++){
if(ind[i]!=outd[i]){
flag=1;
if(outd[i]-ind[i]==1){
cnt1++;
s=i;
}else if(ind[i]-outd[i]==1) cnt2++;
else{
printf("No");
return 0;
}
}
}
if(flag&&!(cnt1==cnt2&&cnt2==1)){
printf("No");
return 0;
}
dfs(s);
for(int i=cnt;i>=1;i--) printf("%d ",r[i]);
return 0;
}
Luogu P1341 无序字母对
转化一下,即以字母为节点,无序字母对间建无向边,询问是否有欧拉路径存在。同样求字典序最小,但此题最多 \(26\) 个字母,可以使用邻结矩阵存储。
#include<iostream>
#include<cstdio>
using namespace std;
int n,minx=60,maxx;
int g[120][120],d[60],r[1010],cnt;
void dfs(int u){
for(int i=minx;i<=maxx;i++){
if(g[u][i]){
g[u][i]=0;g[i][u]=0;
dfs(i);
}
}
r[++cnt]=u;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
char a,b;
int u,v;
cin>>a>>b;
if(a<'a') u=a-'A'+1;
else u=a-'a'+27;
if(b<'a') v=b-'A'+1;
else v=b-'a'+27;
g[u][v]=g[v][u]=1;
minx=min(minx,min(u,v));
maxx=max(maxx,max(u,v));
d[u]++;d[v]++;
}
int s,cnto=0;
bool flag1=0,flag2=0;
for(int i=minx;i<=maxx;i++){
if(d[i]%2){
flag1=1;
if(!flag2){
s=i;
flag2=1;
}
cnto++;
}
}
if(flag1){
if(cnto==2) dfs(s);
else{
printf("No Solution");
return 0;
}
}
else dfs(minx);
if(cnt!=n+1) printf("No Solution");
for(int i=cnt;i>=1;i--){
char c;
if(r[i]<27) c='A'+r[i]-1;
else c='a'+r[i]-27;
printf("%c",c);
}
return 0;
}
Luogu P2731 [USACO3.3] 骑马修栅栏 Riding the Fences
无向图版本。
唯一的不同是要防止边被重复走,走到一条边时要将其删除。
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=510;
int m,minu=520,maxu;
int d[maxn],r[maxn],s,cnt;
int g[maxn][maxn];
void dfs(int u){
for(int i=minu;i<=maxu;i++){
if(g[u][i]){
g[u][i]--,g[i][u]--;
dfs(i);
}
}
r[++cnt]=u;
}
int main(){
scanf("%d",&m);
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
g[u][v]++,g[v][u]++;
d[u]++,d[v]++;
minu=min(minu,min(u,v));
maxu=max(maxu,max(u,v));
}
int flag=0;
for(int i=minu;i<=maxu;i++){
if(d[i]%2){
flag=1;
s=i;
break;
}
}
if(flag) dfs(s);
else dfs(minu);
for(int i=cnt;i>=1;i--) printf("%d\n",r[i]);
return 0;
}
Luogu P1127 词链
在有向图上输出欧拉路径上的边。
字符串的处理与 UVA10129 类似,为字符串首和尾字符间建边。对于字典序限制,只需要为所有字符串和每个点出边排序,DFS 时按顺序遍历。
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
const int M=50;
int n,s=-1;
int ind[M],outd[M];
int fa[M],d[M];
int st[N],top;
string wd[N];
struct Node{
int to,id;
};
vector<Node> g[N];
int Find(int x){
if(fa[x]==x) return x;
else return fa[x]=Find(fa[x]);
}
bool check(){
int p=-1;
for(int i=0;i<26;i++){
if(!ind[i]&&!outd[i]) continue;
if(Find(i)!=p&&(p!=-1)) return 0;
p=fa[i];
}
int cnts=0,cnte=0;
for(int i=0;i<26;i++){
if(ind[i]==outd[i]) continue;
if(outd[i]-ind[i]==1){
cnts++;
if(s==-1) s=i;
}
else if(ind[i]-outd[i]==1) cnte++;
else return 0;
}
return (!cnts&&!cnte)||(cnts==1&&cnte==1);
}
void dfs(int u){
for(int i=d[u];i<g[u].size();i=d[u]){
d[u]=i+1;
dfs(g[u][i].to);
st[++top]=g[u][i].id;
}
}
bool cmp(Node x,Node y){
return x.id<y.id;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=0;i<26;i++) fa[i]=i;
for(int i=1;i<=n;i++) cin>>wd[i];
sort(wd+1,wd+1+n);
for(int i=1;i<=n;i++){
int u=wd[i][0]-'a',v=wd[i][wd[i].size()-1]-'a';
g[u].push_back((Node){v,i});
ind[v]++,outd[u]++;
u=Find(u),v=Find(v);
if(u!=v) fa[u]=v;
}
if(!check()) cout<<"***";
else{
if(s==-1){
for(int i=0;i<26;i++){
if(ind[i]||outd[i]){
s=i;
break;
}
}
}
for(int i=0;i<26;i++) sort(g[i].begin(),g[i].end(),cmp);
dfs(s);
while(top){
cout<<wd[st[top]];
top--;
if(top) cout<<'.';
}
}
return 0;
}
应用 - 图论建模
Codeforces 547D Mike and Fish
题目中要求同一列红点和蓝点数量之差不超过 \(1\)。动用人类智慧,想到以横纵坐标为点,原题的点为边,原题点颜色为边的方向。于是题目就转化为:给定无向图,确定每条边的方向,使得每个点的入度、出度差不超过 \(1\)。
不妨先考虑弱化,若每个点都为偶数度,那么在原图上构造有向图欧拉回路,所有点的入度就都会等于出度。然后考虑有奇点怎么办。不难想到,我们要把奇点的入度、出度差构造为 \(1\)。我们把奇点两两配对连边,使其全部变为偶点,此时可以构造出欧拉回路,所有的点入度等于出度,那么原先的奇点要么多一条出边,要么多一条入边,入度和出度的差就为 \(1\)。
构造欧拉回路的话,维护每个点是否已经过,为走过的边标记一个方向。走完所有节点后,要回到起点,由于题目保证有解,剩下的边就都是反向,用于走回起点。
注意,这种构造方法需要走完一条边删除一条边,才能保证时间复杂度为 \(O(m)\)(\(m\) 为边数)。具体实现很容易,只需要在遍历时同步更改每个节点在邻接表中的头指针。
时间复杂度 \(O(n)\)。
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int n;
int cnt[N],deg[4*N];;
int h[4*N],tot=1;
bool vise[4*N],visn[4*N],ans[4*N];
struct Node{
int to,nxt;
}e[4*N];
void Add(int u,int v){
tot++;
e[tot].to=v;
e[tot].nxt=h[u];
h[u]=tot;
}
void dfs(int u){
visn[u]=1;
for(int& i=h[u];i;i=e[i].nxt){
int v=e[i].to;
if(vise[i]) continue;
ans[i]=vise[i]=vise[i^1]=1;
dfs(v);
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
int x,y;
cin>>x>>y;
y+=N;
cnt[i]=tot+2;
deg[x]++,deg[y]++;
Add(x,y),Add(y,x);
}
int lstu=0;
for(int i=1;i<=2*N;i++){
if(deg[i]%2){
if(!lstu) lstu=i;
else{
Add(i,lstu),Add(lstu,i);
lstu=0;
}
}
}
for(int i=1;i<=2*N;i++){
if(!visn[i]) dfs(i);
}
for(int i=1;i<=n;i++){
if(ans[cnt[i]]) cout<<'b';
else cout<<'r';
}
return 0;
}
Codeforces 527E/528C Data Center Drama
注意到题目要求构造有向图使每个点的出入度都是偶数,即图在定向前每个点度都是偶数,即存在无向图欧拉回路。所以像上个题一样把奇点两两相连。
但存在欧拉回路的图并不都满足定向后每个点的出入度都是偶数。因为一条边会贡献一个出度和一个入度,所以若每个点出入度都是偶数,总边数也必须是偶数。所以若处理完上一步后总边数是奇数,就要随便找一个点连一个自环。
因为所有新增的边都是必要的,所以这样构造边一定是最少的。
然后考虑怎么定向。我们要在访问每个节点的时候为他的入度或出度 \(+2\),那么他的上下相邻两边要么都是出边,要么都是入边。于是我们在搜索时隔一条边换一个方向,即以 \(a→b←c→d←...→a\) 的方式构造。
时间复杂度 \(O(m)\)。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,m,idx;
int h[N],tot=1;
int deg[N];
bool vis[8*N];
struct Node{
int to,nxt;
}e[8*N];
void Add(int u,int v){
tot++;
e[tot].to=v;
e[tot].nxt=h[u];
h[u]=tot;
}
void dfs(int u){
for(int& i=h[u];i;i=e[i].nxt){
if(vis[i]) continue;
vis[i]=vis[i^1]=1;
int v=e[i].to;
dfs(v);
if(idx&1) cout<<v<<' '<<u<<'\n';
else cout<<u<<' '<<v<<'\n';
idx++;
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
deg[u]++,deg[v]++;
Add(u,v),Add(v,u);
}
int las=-1;
for(int i=1;i<=n;i++){
if(deg[i]&1){
if(las==-1) las=i;
else Add(las,i),Add(i,las),las=-1,m++;
}
}
if(m&1) Add(1,1),m++;
cout<<m<<'\n';
dfs(1);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号