【笔记】线段树
一、介绍和功能
线段树是用于维护区间信息的一种常用数据结构,又称区间树。
线段树可以在低复杂度内实现单点查询、单点修改、区间查询(区间求和、求最值等)、区间修改等操作。
一般可以使用线段树的题,序列长度 \(n\) 和修改次数 \(m\) 的范围在几倍 \(10^5\) 左右。
二、构造和性质
线段树将每一个长度不为 \(1\) 的区间分成两半进行维护,分别是大区间的左子树和右子树,通过不断合并子树来求得区间信息。每个叶子结点就是原序列的每一项。
就像这样:
(image from OI-wiki)
而每个区间的表示也很便捷,如在这棵线段树中,\([2,5]\) 区间的表示即为:
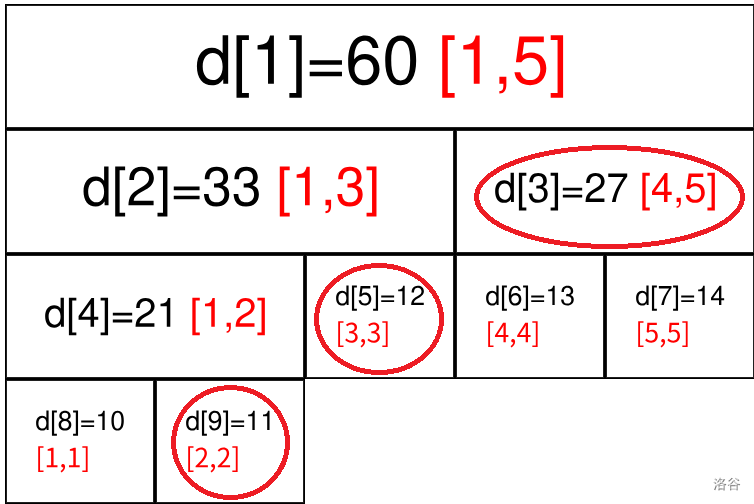
不难发现,一棵线段树就是一棵完全二叉树,因此有以下性质(忽略常数):
- 树高为 \(O(\log n)\)。
- 任意区间都可以用线段树上不超过 \(O(\log n)\) 个结点表示。
- 进行修改时,最多只修改 \(O(\log n)\) 个结点。
- 设一个结点的编号为 \(i\),那么这个结点的左子树根节点编号为 \(2 \times i\),右子树根节点编号为 \(2 \times i+1\)。
三、实现和分析
1. 建树
首先,我们需要把线段树构造出来。(线段树一定要建树!!!)
构造时,首先需要考虑的就是空间问题。根据上文所述,每个叶子结点就是原序列的每一项,所以在最好情况下,所有叶子结点都在同一层,就像这样:
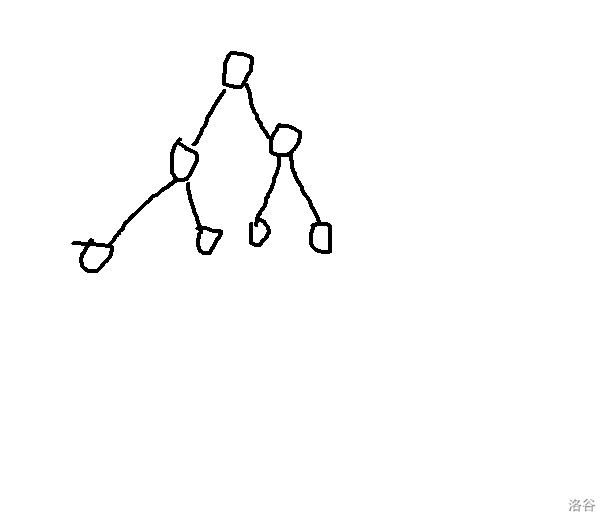
那么叶子结点的数量就是 \(n\)。由此可得非叶子结点的数量为 \(n-1\),那么总结点数量就是 \(2n-1\),存储空间也就是 \(2\) 倍空间。
但这仅仅是最好情况。就如同最开始的那一棵线段树一样,并不是所有叶子结点都在同一层。极端情况下,将会只有一个叶子结点不在最后一层,那么就又会多 \(2n-1\) 个结点,加上上一种情况的 \(2n-1\) 个结点,总数就是 \(4n-2\) 个结点,存储空间需要 \(4\) 倍。
那么数组就要开 \(4\) 倍大小了。
我们用一个结构体来表示这个线段树的每一个结点。每一个结点需要维护的信息都放在结构体里,有区间左端点 \(l\),区间右端点 \(r\),区间信息 \(data\),区间懒标记 \(lazy\)(这个是什么我们一会会讲)等。
然后递归建树,按照 \(2\times i\)、\(2\times i+1\) 的规则建树,每次二分 \(l\) 和 \(r\),直到 \(l=r\) 为止,并把原序列信息放在叶子结点中,剩下的结点按照一定方式求出要维护的信息。时间复杂度 \(O(n)\)。
代码如下(这里以区间求和为例):
void build(int p,int l,int r){//线段树,一定要建树!
tr[p].l=l,tr[p].r=r;
if(l==r){
tr[p].data=a[l];
return;
}
int mid=(l+r)/2;
build(2*p,l,mid);
build(2*p+1,mid+1,r);
tr[p].data=tr[2*p].data+tr[2*p+1].data;
}
维护信息比较复杂时,可以将向上更新封装为一个函数 push_up,便于代码。
2. 单点修改
首先,我们需要找到这个点。我们知道这个点的下标之后,不断二分区间,看它处于左区间还是右区间中,然后继续递归直到找到这个点,并将其修改。
修改完成之后,这个结点的祖先结点也必然发生变化,这时候往上回溯再按照以前的方式求一遍祖先结点的 \(data\) 即可。时间复杂度 \(O(\log n)\)。
代码如下(这里以区间求和为例):
void update(int p,int u,long long k){
if(tr[p].l==tr[p].r&&tr[p].l==u){//找到了
tr[p].data+=k;
return ;
}
int mid=(tr[p].l+tr[p].r)/2;
if(u<=mid) update(2*p,u,k);//判断处于哪个区间中
else update(2*p+1,u,k);
tr[p].data=tr[2*p].data+tr[2*p+1].data;//重新求一遍区间和
}
3. 区间查询
递归遍历,如果当前结点的区间完全在所求区间内,那么直接返回当前区间的信息。如果所求区间的左端点属于当前区间的左子区间那就去遍历左子区间,如果所求区间的右端点属于当前区间的右子区间那就去遍历右子区间。最后把两个结果综合起来即可。时间复杂度 \(O(\log n)\)。
代码如下(这里以区间求和为例):
long long query(int p,int l,int r){
if(l<=tr[p].l&&tr[p].r<=r){
return tr[p].data;
}
int mid=(tr[p].l+tr[p].r)/2;
long long val=0;
if(l<=mid){
val+=query(2*p,l,r);
}
if(r>mid){
val+=query(2*p+1,l,r);
}
return val;
}
有了以上三种操作,你就可以愉快的 AC Luogu P3374【模板】树状数组 1 了。
4. 区间修改
开始上强度。我们知道如果给每一个叶子结点都进行单点修改的话时间复杂度反而比暴力维护要高,不可接受。还记得前文说的懒标记吗?这里就派上用场了。
我们在修改一个区间信息时,并不一定真的要去修改,而是给这个区间打一个标记,在查询区间的时候再进行修改。这种标记称为懒标记。我们仿照区间查询,先找到那个区间,然后给区间的最高级结点全部打上懒标记,在查询时将懒标记下移至叶子结点并进行修改,同时删除懒标记,即可完成修改操作。此时时间复杂度依然为 \(O(\log n)\)。
代码如下(这里以区间求和为例):
void update(int p,int l,int r,long long k){
if(l<=tr[p].l&&tr[p].r<=r){
tr[p].data+=(tr[p].r-tr[p].l+1)*k;
tr[p].lazy+=k;
return;
}
spread(p);//懒标记下移
int mid=(tr[p].l+tr[p].r)/2;
if(mid>=l){
update(2*p,l,r,k);
}
if(mid<r){
update(2*p+1,l,r,k);
}
tr[p].data=tr[2*p].data+tr[2*p+1].data;
}
void spread(int p){
if(tr[p].lazy){
tr[2*p].data+=(tr[2*p].r-tr[2*p].l+1)*tr[p].lazy;
tr[2*p+1].data+=(tr[2*p+1].r-tr[2*p+1].l+1)*tr[p].lazy;
tr[2*p].lazy+=tr[p].lazy;
tr[2*p+1].lazy+=tr[p].lazy;
tr[p].lazy=0;
}
}
spread 函数也有一个更常用的名字:push_down。
5. 单点查询
把单点修改和区间查询杂交一下就可以了。当然也可以查询一个左端点与右端点相同的区间。
long long query(int p,int u){
long long ans=0;
if(tr[p].l==tr[p].r){
ans=tr[p].data;
return ans;
}
spread(p);
int mid=(tr[p].l+tr[p].r)/2;
if(u<=mid){
ans+=query(p*2,u);
}else ans+=query(2*p+1,u);
return ans;
}
至此线段树的基本操作已经全部讲完,可以愉快的 AC Luogu P3368【模板】树状数组 2 和 Luogu P3372【模板】线段树 1(这个题区间查询别忘了加懒标记下移) 了。
附:结构体封装线段树模板
struct Node{
int data,lazy,l,r;//Add more operations here
};
struct Segtr{
Node tr[4*N];
void push_up(int p){
tr[p].data=tr[2*p].data+tr[2*p+1].data;
//Add more operations here
}
void push_down(int p){
if(tr[p].lazy){
tr[2*p].data+=(tr[2*p].r-tr[2*p].l+1)*tr[p].lazy;
tr[2*p+1].data+=(tr[2*p+1].r-tr[2*p+1].l+1)*tr[p].lazy;
tr[2*p].lazy+=tr[p].lazy;
tr[2*p+1].lazy+=tr[p].lazy;
//Add more operations here
tr[p].lazy=0;
}
}
void build(int p,int l,int r){
tr[p].l=l,tr[p].r=r;
if(l==r){
tr[p].data=0;
//Add more operations here
return ;
}
int mid=(l+r)>>1;
build(2*p,l,mid);
build(2*p+1,mid+1,r);
push_up(p);
}
void update(int p,int l,int r,int k){
if(l<=tr[p].l&&tr[p].r<=r){
tr[p].data+=(tr[p].r-tr[p].l+1)*k;
tr[p].lazy+=k;
//Add more operations here
return ;
}
push_down(p);
int mid=(l+r)>>1;
if(l<=mid) update(2*p,l,r,k);
if(mid<r) update(2*p+1,l,r,k);
push_up(p);
}
int query(int p,int l,int r){
int val=0;
if(l<=tr[p].l&&tr[p].r<=r){
return tr[p].data;//Add more operations here
}
push_down(p);
int mid=(tr[p].l+tr[p].r)>>1;
if(l<=mid){
val+=query(2*p,l,r);
//Add more operations here
}
if(r>mid){
val+=query(2*p+1,l,r);
//Add more operations here
}
return val;
}
}seg;
通常来说不用单独写单点修改和查询,因为单点就相当于 \(l=r\) 的区间。
四、实际和应用
Luogu P3373【模板】线段树 2
这个题涉及加与乘两种操作,那么懒标记应该打两个。
这时候有个问题就出现了,怎样才能确保运算的顺序。不难发现,对一个已经加过的区间再乘一个值,那么加的值也得跟着乘。那么这样就好办了,我们在加操作时直接增加加懒标记 \(add\),在乘操作时把乘懒标记 \(mul\) 和加懒标记 \(add\) 一起乘。
还有一个地方需要注意,就是懒标记下移时的运算顺序问题,我们需要先乘后加,因为加懒标记中已经包含了乘的值,如果再乘加懒标记那就超过了原本的值。
最后记得在建树的时候给 \(mul\) 初始赋成 \(1\)。另外,long long 类型变量在取模时,模数一定要开 long long(血的教训)。
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=1e5+10;
struct Node{
int l,r;
long long data,add,mul;
}tr[4*maxn];
int n,q;
long long m;
long long a[maxn];
void build(int p,int l,int r){//线段树,一定要建树!
tr[p].l=l,tr[p].r=r;
tr[p].mul=1;
if(l==r){
tr[p].data=a[l];
return;
}
int mid=(l+r)/2;
build(2*p,l,mid);
build(2*p+1,mid+1,r);
tr[p].data=(tr[2*p].data+tr[2*p+1].data)%m;
}
void spread(int p){
if(tr[p].mul!=1){
tr[2*p].data=(tr[2*p].data*tr[p].mul)%m;
tr[2*p+1].data=(tr[2*p+1].data*tr[p].mul)%m;
tr[2*p].add=(tr[2*p].add*tr[p].mul)%m;
tr[2*p+1].add=(tr[2*p+1].add*tr[p].mul)%m;
tr[2*p].mul=(tr[2*p].mul*tr[p].mul)%m;
tr[2*p+1].mul=(tr[2*p+1].mul*tr[p].mul)%m;
tr[p].mul=1;
}
if(tr[p].add){
tr[2*p].data=(tr[2*p].data+(tr[2*p].r-tr[2*p].l+1)*tr[p].add)%m;
tr[2*p+1].data=(tr[2*p+1].data+(tr[2*p+1].r-tr[2*p+1].l+1)*tr[p].add)%m;
tr[2*p].add=(tr[2*p].add+tr[p].add)%m;
tr[2*p+1].add=(tr[2*p+1].add+tr[p].add)%m;
tr[p].add=0;
}
}
void change(int p,int l,int r,long long k,int op){
if(l<=tr[p].l&&tr[p].r<=r){
if(op==2){
tr[p].data=(tr[p].data+(tr[p].r-tr[p].l+1)*k)%m;
tr[p].add=(tr[p].add+k)%m;
return;
}else if(op==1){
tr[p].add=(tr[p].add*k)%m;
tr[p].mul=(tr[p].mul*k)%m;
tr[p].data=(tr[p].data*k)%m;
return;
}
}
spread(p);
int mid=(tr[p].l+tr[p].r)/2;
if(mid>=l){
change(2*p,l,r,k,op);
}
if(mid<r){
change(2*p+1,l,r,k,op);
}
tr[p].data=(tr[2*p].data+tr[2*p+1].data)%m;
}
long long ask(int p,int l,int r){
if(l<=tr[p].l&&tr[p].r<=r){
return tr[p].data;
}
spread(p);
int mid=(tr[p].l+tr[p].r)/2;
long long val=0;
if(l<=mid){
val=(val+ask(2*p,l,r)%m)%m;
}
if(r>mid){
val=(val+ask(2*p+1,l,r)%m)%m;
}
return val%m;
}
int main(){
scanf("%d%d%d",&n,&q,&m);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
}
build(1,1,n);
for(int i=1;i<=q;i++){
int op,a,b,k;
scanf("%d%d%d",&op,&a,&b);
if(op==1){
scanf("%d",&k);
change(1,a,b,k,1);
}else if(op==2){
scanf("%d",&k);
change(1,a,b,k,2);
}else{
printf("%lld\n",ask(1,a,b));
}
}
return 0;
}
Luogu P2357 守墓人、P2068 统计和、P1531 I Hate It
三个板子题,选择模板进行组合即可。
Luogu P1198 [JSOI2008] 最大数
这个题要求我们维护一个区间最大值,这个改一下板子就行。重点来说一下插入操作。我们先建一个空树(或者不建树,在后面添加的时候再把区间信息加上去),然后维护一个变量 \(tot\) 代表序列中有多少个项,每次在第 \(tot+1\) 个叶子结点中进行修改即可完成添加操作。
#include<iostream>
#include<cstdio>
#define int long long
using namespace std;
const int maxn=2e5+10;
struct Node{
int l,r;
int data;
}tr[4*maxn];
int tot,m,d,t;
void build(int p,int l,int r){
tr[p].l=l;tr[p].r=r;
if(l==r){
return;
}
int mid=(l+r)/2;
build(2*p,l,mid);
build(2*p+1,mid+1,r);
tr[p].data=max(tr[2*p].data%d,tr[2*p+1].data%d);
}
void change(int p,int u,long long k){
if(tr[p].l==tr[p].r){
tr[p].data=k%d;
return;
}
int mid=(tr[p].l+tr[p].r)/2;
if(u<=mid) change(2*p,u,k);
else change(2*p+1,u,k);
tr[p].data=max(tr[2*p].data%d,tr[2*p+1].data%d);
}
long long ask(int p,int l,int r){
if(l<=tr[p].l&&tr[p].r<=r){
return tr[p].data;
}
long long ans=-9223372036854775807;
int mid=(tr[p].l+tr[p].r)/2;
if(l<=mid) ans=max(ans,ask(p*2,l,r)%d)%d;
if(r>mid) ans=max(ans,ask(p*2+1,l,r)%d)%d;
return ans;
}
signed main(){
scanf("%lld%lld",&m,&d);
build(1,1,m);
for(int i=1;i<=m;i++){
char c[2];
scanf("%s",c);
if(c[0]=='Q'){
int l;
scanf("%lld",&l);
t=ask(1,tot-l+1,tot);
printf("%lld\n",t);
}else if(c[0]=='A'){
int n;
scanf("%lld",&n);
change(1,++tot,n+t);
}
}
return 0;
}
Luogu P4588 [TJOI2018] 数学计算
思维非常巧妙的一个题。
不难发现所有的乘数构成了一个序列,操作一就是在这个序列后面不断加数,然后求积。至于操作二,可以转化为把第 \(pos\) 个乘数变成了一,然后重新求积。
我们发现这就构成了一个单点查询单点修改的线段树,每个叶子结点是乘数,而结点维护的是区间乘积,要求的就是根节点。想到了这点,代码就很好写了。
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=1e5+10;
struct Node{
int l,r;
long long data;
}tr[4*maxn];
int T;
int n,q;
long long m;
long long a[maxn];
void build(int p,int l,int r){//线段树,一定要建树!
tr[p].l=l,tr[p].r=r;
if(l==r){
tr[p].data=1;
return;
}
int mid=(l+r)/2;
build(2*p,l,mid);
build(2*p+1,mid+1,r);
tr[p].data=(tr[2*p].data*tr[2*p+1].data)%m;
}
void change(int p,int u,long long k){
if(tr[p].l==tr[p].r&&tr[p].l==u){
tr[p].data=k;
return ;
}
int mid=(tr[p].l+tr[p].r)/2;
if(u<=mid) change(2*p,u,k);
else change(2*p+1,u,k);
tr[p].data=(tr[2*p].data*tr[2*p+1].data)%m;
}
int main(){
scanf("%d",&T);
while(T--){
scanf("%d%d",&q,&m);
build(1,1,q);
for(int i=1;i<=q;i++){
int op,k;
scanf("%d",&op);
if(op==1){
scanf("%d",&k);
change(1,i,k);
}else if(op==2){
scanf("%d",&k);
change(1,k,1);
}
printf("%lld\n",tr[1].data%m);
}
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号