第二次博客作业
前言:
PTA题目集4:题目量并不是很多,第一和第三都不是很有难度。
PTA题目集5:题目难度骤然提升,很考验对类的构建和数学知识的运用。(;´д`)ゞ
期中考试:难度不是很大。( ̄y▽, ̄)╭
设计与分析:
7-2 点线形系列4-凸四边形的计算
用户输入一组选项和数据,进行与四边形有关的计算。
以下四边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
1:输入四个点坐标,判断是否是四边形、平行四边形,判断结果输出true/false,结果之间以一个英文空格符分隔。
2:输入四个点坐标,判断是否是菱形、矩形、正方形,判断结果输出true/false,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
3:输入四个点坐标,判断是凹四边形(false)还是凸四边形(true),输出四边形周长、面积,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
4:输入六个点坐标,前两个点构成一条直线,后四个点构成一个四边形或三角形,输出直线与四边形(也可能是三角形)相交的交点数量。如果交点有两个,再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积(不换行)。若直线与四边形或三角形的一条边线重合,输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入,输出"not a quadrilateral or triangle"。
后四个点构成三角形的情况:假设三角形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z 不与xy都相邻,如z x y s、x z s y、x s z y
5:输入五个点坐标,输出第一个是否在后四个点所构成的四边形(限定为凸四边形,不考虑凹四边形)或三角形(判定方法见选项4)的内部(若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。如果点在多边形的某条边上,输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形,输出"not a quadrilateral or triangle"。
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
注意:输出的数据若小数点后超过3位,只保留小数点后3位,多余部分采用四舍五入规则进到最低位。小数点后若不足3位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333,1.0按格式输出为1.0
选项1、2、3中,若四边形四个点中有重合点,输出"points coincide"。
选项4中,若前两个输入线的点重合,输出"points coincide"。
输入样例1:
选项1,点重合。例如:
1:-1,-1 -1,-1 1,2 1,-2输出样例:
在这里给出相应的输出。例如:
points coincide输入样例2:
不符合基本格式。例如:
1:-1,-1 1,2 -1,1 ++1,0输出样例:
在这里给出相应的输出。例如:
Wrong Format输入样例3:
选项1,输入点数量不对。例如:
1:-1,-1 -1,2 输出样例:
在这里给出相应的输出。例如:
wrong number of points输入样例4:
选项1,正确输入判断。例如:
1:-1,-1 -1,1 1,2 1,-2输出样例:
在这里给出相应的输出。例如:
true false输入样例5:
选项2,输入点不构成四边形。例如:
2:10,10 1,1 0,0 1,20输出样例:
在这里给出相应的输出。例如:
not a quadrilateral输入样例6:
选项2,正方形。例如:
2:0,0 0,80 80,80 80,0输出样例:
在这里给出相应的输出。例如:
true true true输入样例7:
选项2。例如:
2:0,0 -10,80 0,160 -10,80输出样例:
在这里给出相应的输出。例如:
not a quadrilateral输入样例8:
选项3,凸四边形。例如:
3:-1,-1 -1,1 1,2 1,-2输出样例:
在这里给出相应的输出。例如:
true 10.472 6.0输入样例9:
选项3,。例如:
3:0,0 -10,100 0,99 10,100输出样例:
在这里给出相应的输出。例如:
false 221.097 990.0其余样例,详见附件:
类图:
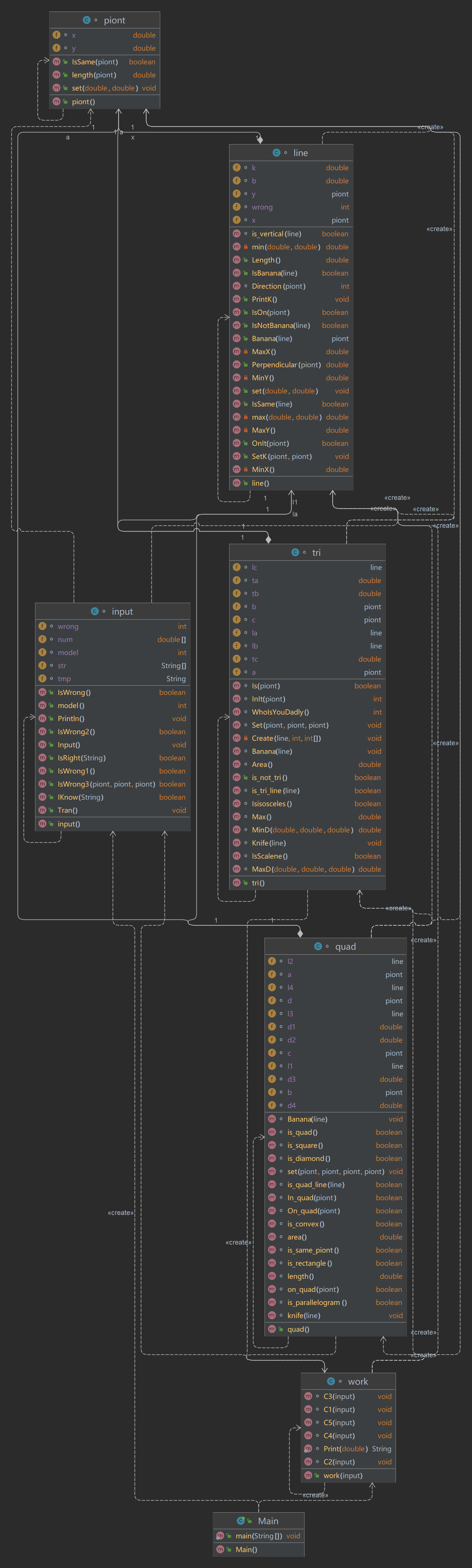
代码软件分析:
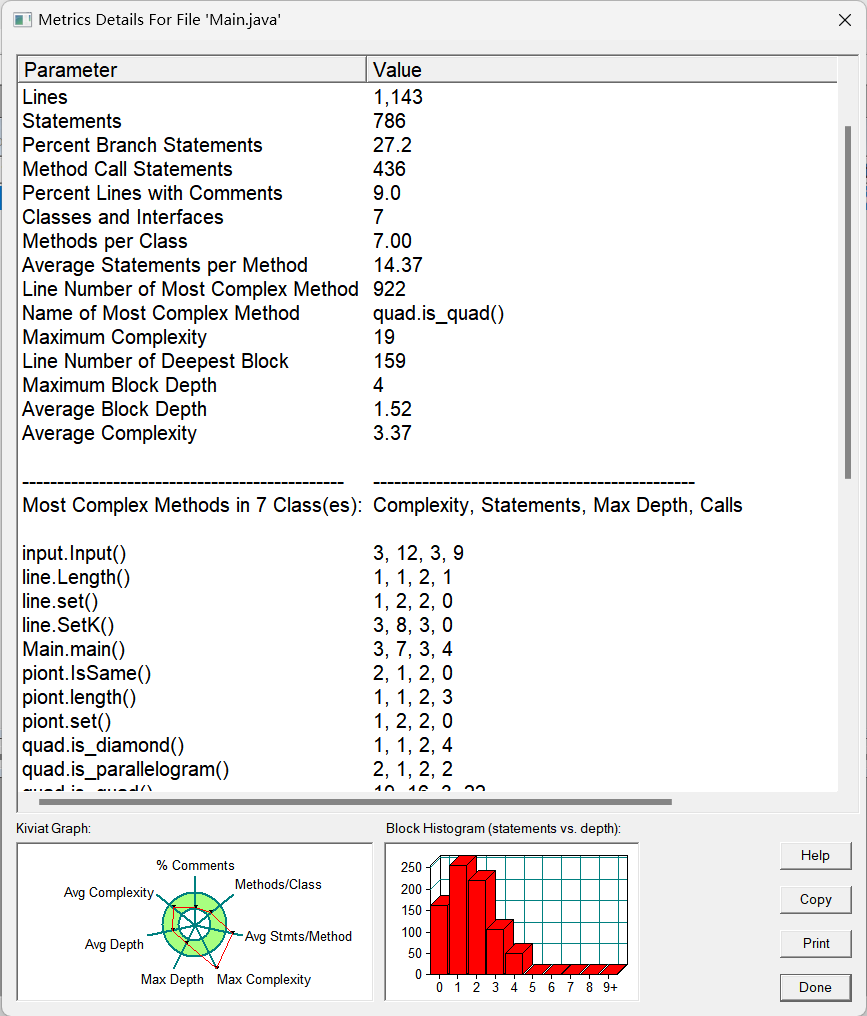
核心代码分析
四边形类
public class quad {
piont a, b, c, d;
line l1, l2, l3, l4;
double d1, d2, d3, d4;
//设置四边形初始化
void set(piont a, piont b, piont c, piont d) {
this.a = a;
this.b = b;
this.c = c;
this.d = d;
l1 = new line();
l1.SetK(a, b);
l2 = new line();
l2.SetK(b, c);
l3 = new line();
l3.SetK(c, d);
l4 = new line();
l4.SetK(d, a);
d1 = l1.Length();
d2 = l2.Length();
d3 = l3.Length();
d4 = l4.Length();
}
//判断是不是四边形
boolean is_quad() {
if (l1.IsSame(l2) || l1.IsSame(l3) || l1.IsSame(l4) || l2.IsSame(l3) || l2.IsSame(l4) || l3.IsSame(l4))
return false;
if (!l1.IsNotBanana(l3) && !l2.IsNotBanana(l4)) {
piont a = l1.Banana(l3);
piont b = l2.Banana(l4);
if (((l1.IsOn(a) && l3.IsOn(a)) || (l2.IsOn(b) && l4.IsOn(b))))
return false;
}
if (!l1.IsNotBanana(l3)) {
piont b = l1.Banana(l3);
if ((l1.IsOn(b) && l3.IsOn(b)))
return false;
}
if (!l2.IsNotBanana(l4)) {
piont a = l2.Banana(l4);
if ((l2.IsOn(a) && l4.IsOn(a)))
return false;
}
return true;
}
//判断是不是平行四边形
boolean is_parallelogram() {
return l1.IsNotBanana(l3) && l2.IsNotBanana(l4);
}
//判断是否菱形
boolean is_diamond() {
return is_parallelogram() && (l1.Length() == l2.Length() && l2.Length() == l3.Length() && l3.Length() == l4.Length());
}
//判断是否矩形
boolean is_rectangle() {
return is_parallelogram() && (l1.is_vertical(l2) && l2.is_vertical(l3));
}
//判断是否正方形
boolean is_square() {
return is_rectangle() && (l1.Length() == l2.Length() && l2.Length() == l3.Length() && l3.Length() == l4.Length());
}
//判断构成四边形是否相同点
boolean is_same_piont() {
return a.IsSame(b) || a.IsSame(c) || a.IsSame(d) || b.IsSame(c) || b.IsSame(d) || c.IsSame(d);
}
//判断是否凸四边形
boolean is_convex() {
tri tri1 = new tri();
tri tri2 = new tri();
tri tri3 = new tri();
tri tri4 = new tri();
tri1.Set(a, b, c);
tri2.Set(c, d, a);
tri3.Set(b, c, d);
tri4.Set(d, a, b);
return Math.abs((tri1.Area() + tri2.Area()) - (tri3.Area() + tri4.Area())) < 1e-6;
}
//四边形面积
double area() {
// 海伦公式只可以求圆内接四边形的面积,高中数学老师讲过。QAQ
// if (is_convex()) {
// double p = (d1 + d2 + d3 + d4) / 2;
// return Math.sqrt((p - d1) * (p - d2) * (p - d3) * (p - d4));
// }
tri tri1 = new tri();
tri tri2 = new tri();
tri tri3 = new tri();
tri tri4 = new tri();
tri1.Set(a, b, c);
tri2.Set(a, c, d);
tri3.Set(c, b, d);
tri4.Set(a, b, d);
double area1 = tri1.Area() + tri2.Area();
double area2 = tri3.Area() + tri4.Area();
if (area1 > area2)
return area2;
else
return area1;
}
//四边形周长
double length() {
return d1 + d2 + d3 + d4;
}
//判断点是否在四边形上
boolean on_quad(piont ace) {
return l1.IsOn(ace) || l2.IsOn(ace) || l3.IsOn(ace) || l4.IsOn(ace);
}
//判断点是否在四边形内部
boolean In_quad(piont ace) {
return l1.Direction(ace) == -l3.Direction(ace) && l2.Direction(ace) == -l4.Direction(ace) && l1.Direction(ace) != 0 && l2.Direction(ace) != 0;
}
//判断点是否在四边形上
boolean On_quad(piont ace) {
return l1.IsOn(ace) || l2.IsOn(ace) || l3.IsOn(ace) || l4.IsOn(ace);
}
// 判断线是否参与构成四边形
boolean is_quad_line(line line) {
return line.IsSame(l1) || line.IsSame(l2) || line.IsSame(l3) || line.IsSame(l4);
}
// 四边形与线交点相关
void Banana(line line) {
int tmp = 0;
piont[] pionts = new piont[4];
if (!l1.IsNotBanana(line)) {
piont p1 = l1.Banana(line);
if (l1.IsOn(p1))
pionts[tmp++] = p1;
}
if (!l2.IsNotBanana(line)) {
piont p1 = l2.Banana(line);
if (l2.IsOn(p1))
pionts[tmp++] = p1;
}
if (!l3.IsNotBanana(line)) {
piont p1 = l3.Banana(line);
if (l3.IsOn(p1))
pionts[tmp++] = p1;
}
if (!l4.IsNotBanana(line)) {
piont p1 = l4.Banana(line);
if (l4.IsOn(p1))
pionts[tmp++] = p1;
}
if (tmp == 0) {
System.out.println("0");
System.exit(0);
}
if (tmp == 1) {
System.out.println("1");
System.exit(0);
}
line line1 = new line();
if (!pionts[0].IsSame(pionts[1]))
line1.SetK(pionts[0], pionts[1]);
else if (!pionts[0].IsSame(pionts[2]))
line1.SetK(pionts[0], pionts[2]);
else if (!pionts[0].IsSame(pionts[3]))
line1.SetK(pionts[0], pionts[3]);
knife(line1);
}
// 直线切割四边形并输出
void knife(line line) {
int da, db, dc, dd, t1 = 0, t2 = 0, t3 = 0;
// 点在线的哪一侧 -1上 0线上 1下
da = line.Direction(a);
db = line.Direction(b);
dc = line.Direction(c);
dd = line.Direction(d);
int[] num = {da, db, dc, dd};
//点在上 线上 下的数目
int[] up = new int[4], on = new int[4], down = new int[4];
piont[] pionts = {a, b, c, d};
piont[] ups = new piont[4], ons = new piont[4], downs = new piont[4];
for (int i = 0; i < 4; i++)
switch (num[i]) {
case -1:
up[t1] = num[i];
ups[t1++] = pionts[i];
break;
case 0:
on[t2] = num[i];
ons[t2++] = pionts[i];
break;
case 1:
down[t3] = num[i];
downs[t3++] = pionts[i];
break;
}
double s1 = 0.0;
if (t1 == 1 && t3 == 1 && t2 == 2)//1,1 切成两个三角形
s1 = line.Perpendicular(ups[t1 - 1]) * line.Length() / 2;
else if (t1 == 2 && t3 == 2) //切成两个四边形
{
quad quad = new quad();
quad.set(line.y, line.x, ups[0], ups[1]);
if (!quad.is_quad()) {
quad.set(line.x, line.y, ups[0], ups[1]);
}
s1 = quad.area();
} else if (t1 == 1)//切成一个三角形一个四边形
s1 = line.Perpendicular(ups[t1 - 1]) * line.Length() / 2;
else if (t3 == 1)
s1 = line.Perpendicular(downs[t3 - 1]) * line.Length() / 2;
double s2 = this.area() - s1;
if (s1 >= s2) {
System.out.println("2 " + work.Print(s2) + " " + work.Print(s1));
} else
System.out.println("2 " + work.Print(s1) + " " + work.Print(s2));
}
}总的来说还是上一道题的切割思路,思路可以移步第一次博客。
7-1 点线形系列5-凸五边形的计算-1
用户输入一组选项和数据,进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
1:输入五个点坐标,判断是否是五边形,判断结果输出true/false。
2:输入五个点坐标,判断是凹五边形(false)还是凸五边形(true),如果是凸五边形,则再输出五边形周长、面积,结果之间以一个英文空格符分隔。 若五个点坐标无法构成五边形,输出"not a pentagon"
3:输入七个点坐标,前两个点构成一条直线,后五个点构成一个凸五边形、凸四边形或凸三角形,输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个,再按面积从小到大输出被直线分割成两部分的面积(不换行)。若直线与多边形形的一条边线重合,输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入,若前两点重合,输出"points coincide"。
以上3选项中,若输入的点无法构成多边形,则输出"not a polygon"。输入的五个点坐标可能存在冗余,假设多边形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如:x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z不与xy都相邻,如:z x y s、x z s y、x s z y
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
注意:输出的数据若小数点后超过3位,只保留小数点后3位,多余部分采用四舍五入规则进到最低位。小数点后若不足3位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333,1.0按格式输出为1.0
输入样例1:
选项1,点重合。例如:
1:-1,-1 1,2 -1,1 1,0输出样例:
在这里给出相应的输出。例如:
wrong number of points详细信息及样例请查看附件,本题包含附件中的选项1-3的功能:
类图
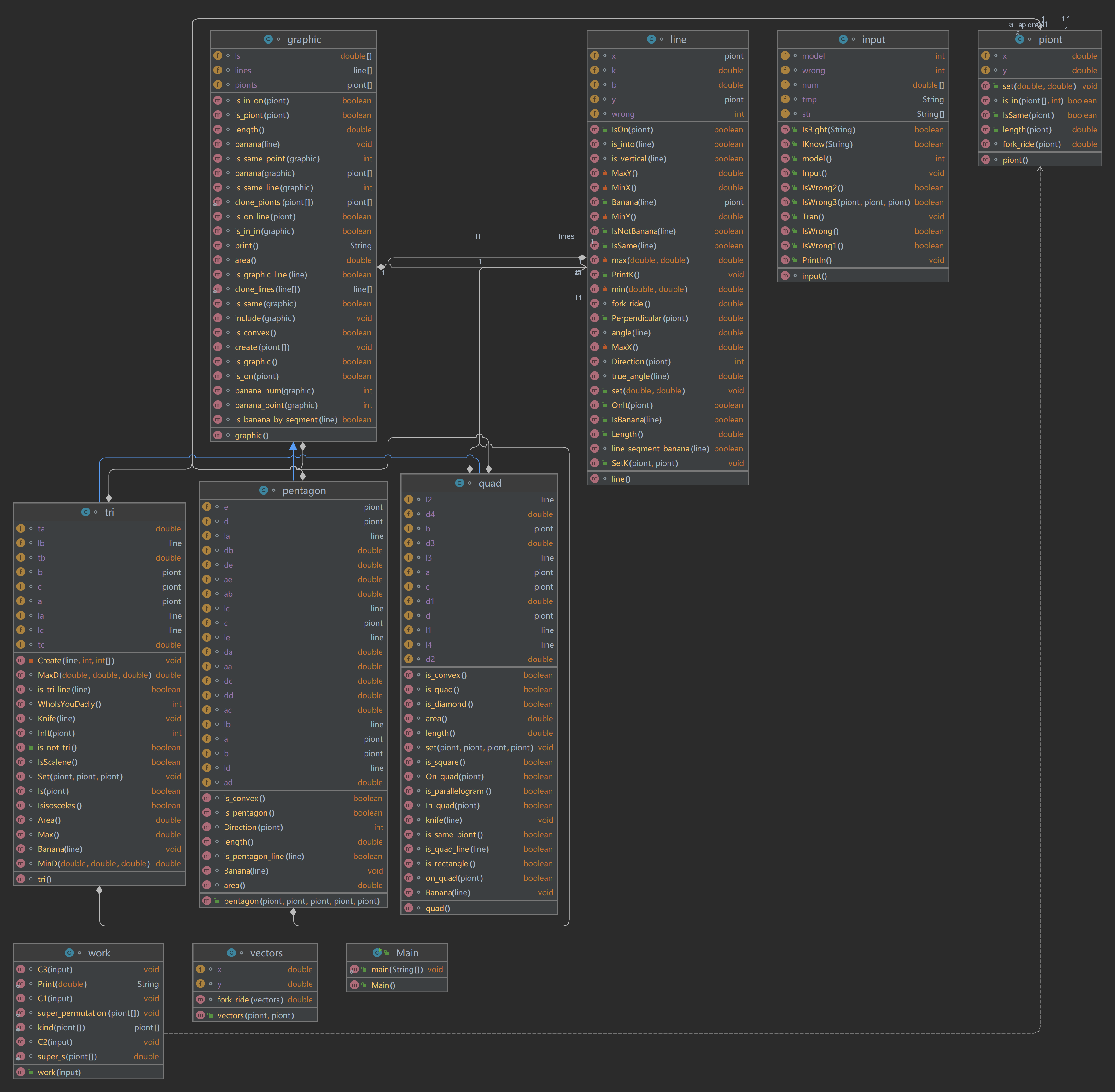
软件分析
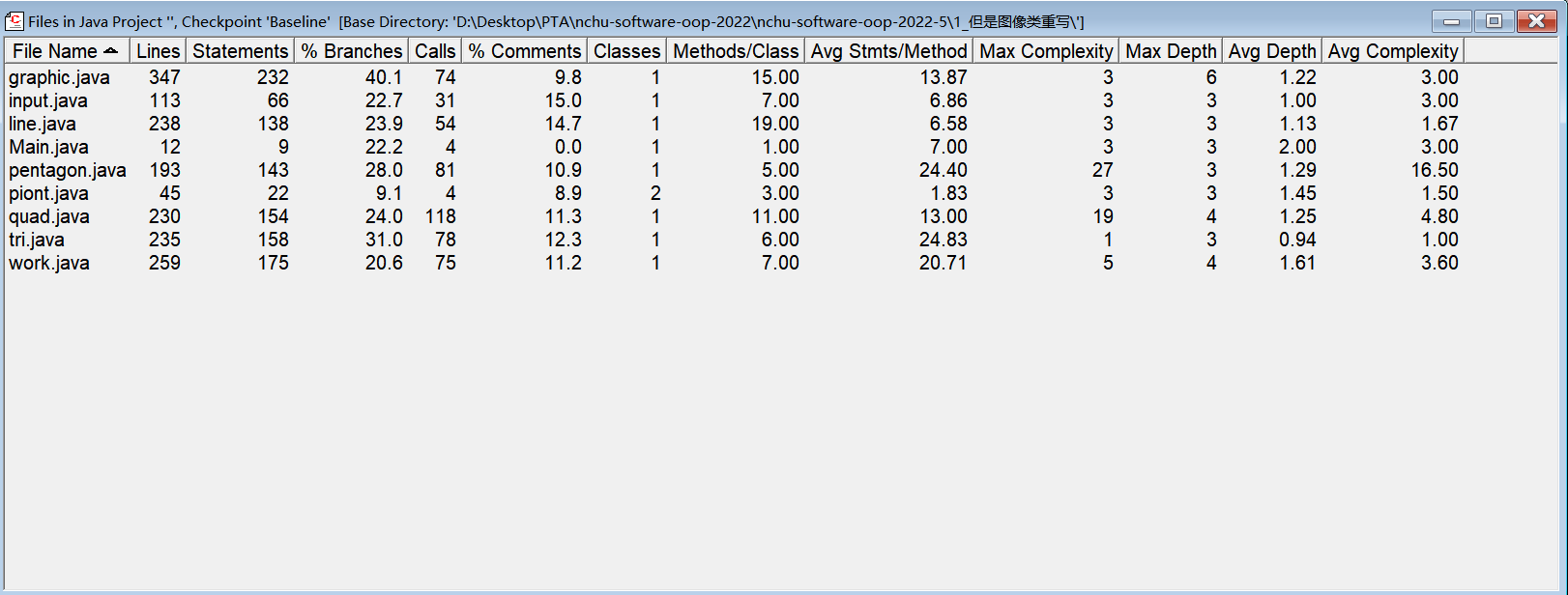
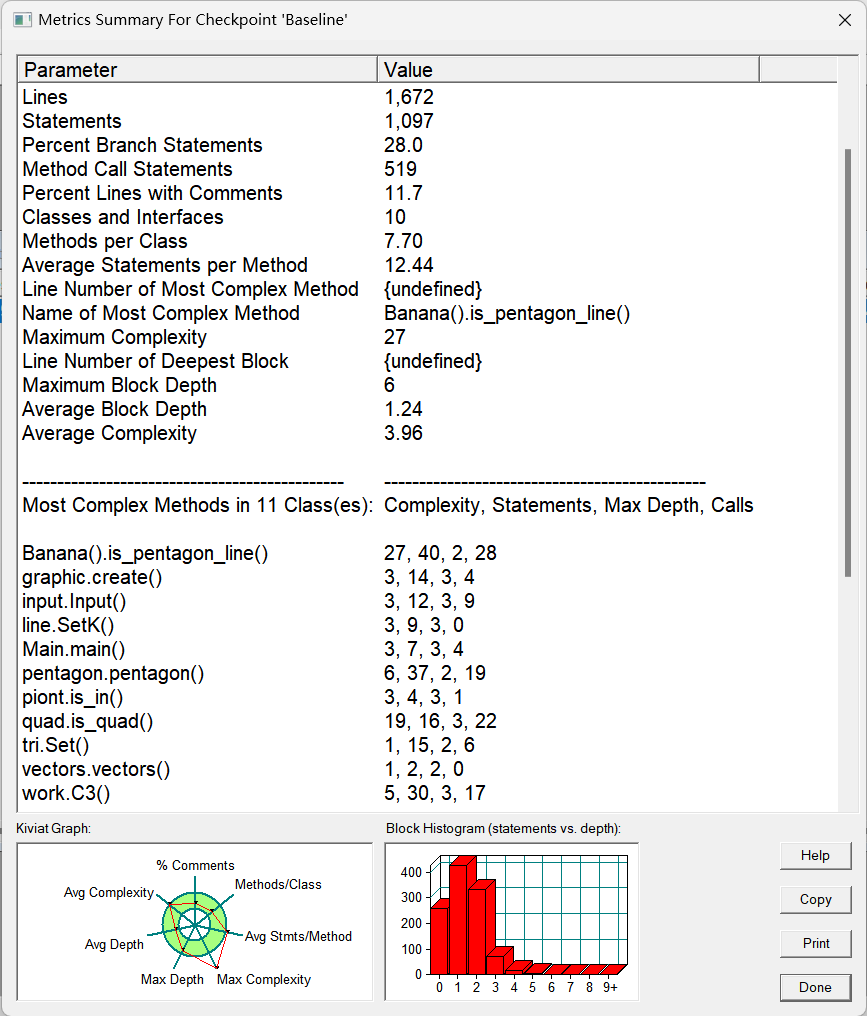
核心代码
鞋带定理求面积
//鞋带定理求面积
//https://zhuanlan.zhihu.com/p/110025234
static double super_s(piont[] psii) {
//多边形面积
double sum = 0;
//临时变量
double xTmp = 0;
double yTmp = 0;
//无论从哪开始第一个坐标的x,y必须是0,0 如果不从0,0 那么会出现误差
double xFirst = 0.0;
double yFirst = 0.0;
// 坐标必须封闭 从哪开始 到哪结束
piont[] psi = graphic.clone_pionts(psii);
work.super_permutation(psi);
piont[] ps = new piont[psi.length + 1];
for (int i = 0; i < ps.length; i++) {
if (i != ps.length - 1)
ps[i] = psi[i];
else
ps[i] = psi[0];
}
String[] arrs = new String[ps.length];
for (int i = 0; i < ps.length; i++)
arrs[i] = ps[i].x + "," + ps[i].y;
// String[] arrs = {"10,10", "40,10", "40,40", "10,40", "10,10"};
for (String s : arrs) {
// 读取当前坐标的x和y
String[] arr = s.split(",");
double xCurrent = Double.parseDouble(arr[0]);
double yCurrent = Double.parseDouble(arr[1]);
/*
* 计算面积:
* (xTmp,yTmp)代表上一行的坐标值
* (xCurrent,yCurrent)代表当前这一行的坐标值
*/
// 公式 sum += ((xTmp - xCurrent) * (yTmp + yCurrent)) * 0.5;
BigDecimal sub = new BigDecimal(xTmp).subtract(new BigDecimal(xCurrent));
BigDecimal add = new BigDecimal(yTmp).add(new BigDecimal(yCurrent));
BigDecimal mul = sub.multiply(add).multiply(new BigDecimal("0.5"));
sum = mul.add(new BigDecimal(sum)).doubleValue();
//计算完面积后,进入下一次循环前需要将“当前坐标”交换为“上一行的坐标”
xTmp = xCurrent;
yTmp = yCurrent;
}
//用最后读取的坐标与第一次读取的坐标进行一次面积运算
BigDecimal sub = new BigDecimal(xTmp).subtract(new BigDecimal(xFirst));
BigDecimal add = new BigDecimal(yTmp).add(new BigDecimal(yFirst));
BigDecimal mul = sub.multiply(add).multiply(new BigDecimal("0.5"));
sum = mul.add(new BigDecimal(sum)).doubleValue();
return Math.abs(sum);
}判断输入图形类型
//输入5点点组,输出 三角形、五边形、四边形点组
static piont[] kind(piont[] ps1) {
int k = 0, num = 0;
piont[] pionts = new piont[5];
piont[] ps = graphic.clone_pionts(ps1);
pionts[k++] = ps[0];
if (!ps[1].IsSame(pionts[0]))
pionts[k++] = ps[1];
if (!ps[2].IsSame(ps[0]) && !ps[2].IsSame(ps[1]))
pionts[k++] = ps[2];
if (!ps[3].IsSame(ps[0]) && !ps[3].IsSame(ps[1]) && !ps[3].IsSame(ps[2]))
pionts[k++] = ps[3];
if (!ps[4].IsSame(ps[0]) && !ps[4].IsSame(ps[1]) && !ps[4].IsSame(ps[2]) && !ps[4].IsSame(ps[3]))
pionts[k++] = ps[4];
if (k == 3)
return new piont[]{pionts[0], pionts[1], pionts[2]};
else if (k == 4)
return new piont[]{pionts[0], pionts[1], pionts[2], pionts[3]};
else {
// a0 b1 c2 d3 e4
line ac = new line();
ac.SetK(pionts[0], pionts[2]);
line bd = new line();
bd.SetK(pionts[1], pionts[3]);
line ce = new line();
ce.SetK(pionts[2], pionts[4]);
line da = new line();
da.SetK(pionts[3], pionts[0]);
line eb = new line();
eb.SetK(pionts[4], pionts[1]);
piont[] psv = new piont[5];//装是顶点的点
int psvk = 0;
if (!eb.IsOn(pionts[0]))
psv[psvk++] = pionts[0];
if (!ac.IsOn(pionts[1]))
psv[psvk++] = pionts[1];
if (!bd.IsOn(pionts[2]))
psv[psvk++] = pionts[2];
if (!ce.IsOn(pionts[3]))
psv[psvk++] = pionts[3];
if (!da.IsOn(pionts[4]))
psv[psvk++] = pionts[4];
if (psvk == 3)//三角形
return new piont[]{psv[0], psv[1], psv[2]};
else if (psvk == 4)//四边形
return new piont[]{psv[0], psv[1], psv[2], psv[3]};
else if (psvk == 5)
return new piont[]{psv[0], psv[1], psv[2], psv[3], psv[4]};//五边形
// else //if (psvk == 6)
// return new piont[]{psv[0], psv[1], psv[2], psv[3], psv[4], psv[5]};//五边形
else {
System.out.println("not a polygon");
System.exit(0);
}
}
return null;
}多边形类代码
class graphic {
// 所有图形类的父类
piont[] pionts;//顶点集
line[] lines;//线集
double[] ls;//线段长度
void create(piont[] pionts1) {
piont[] pionts = graphic.clone_pionts(pionts1);
this.pionts = pionts;
int num = 0;
line[] lines1 = new line[this.pionts.length];
for (int i = 0; i < pionts.length; i++) {
line line = new line();
line.SetK(pionts[i], pionts[(i + 1) % (pionts.length)]);
lines1[num++] = line;
}
lines = lines1;
int k = 0;
double[] lss = new double[lines.length];
for (line line : lines)
lss[k++] = line.Length();
ls = lss;
}
//判断是否构成多边形
boolean is_graphic() {
if (this.pionts.length == 5) {
piont[] kind = work.kind(this.pionts);
if (kind.length != this.pionts.length)
return false;
}
if (this.lines.length < 3)
return false;
if (this.lines.length == 3) {
line line1 = new line();
line line2 = new line();
line1.SetK(pionts[0], pionts[1]);
line2.SetK(pionts[1], pionts[2]);
return !line1.IsSame(line2);
}
for (int i = 0; i < this.lines.length; i++) {
for (int j = 0; j < this.lines.length; j++) {
if (i != j)
// 非相邻边不相交
if (j != (i + 1) % this.lines.length && j != (i - 1 + this.lines.length) % this.lines.length) {
if (this.lines[i].line_segment_banana(this.lines[j]))
return false;
// 临边不平行
else if (j == (i + 1) % this.lines.length || j == (i - 1 + this.lines.length) % this.lines.length) {
if (this.lines[i].IsNotBanana(this.lines[j]))
return false;
}
}
}
}
return true;
}
//判断是否凸多边形
boolean is_convex() {
piont[] ps = clone_pionts(pionts);
vectors[] vs = new vectors[lines.length];
int k = 0;
for (int i = 0; i < ps.length; i++) {
vectors v = new vectors(ps[i], ps[(i + 1) % ps.length]);
vs[k++] = v;
}
double mult = 0.0;
for (int i = 0; i < k; i++) {
if (mult * vs[i].fork_ride(vs[(i + 1) % vs.length]) < 0)
return false;
mult = vs[i].fork_ride(vs[(i + 1) % vs.length]);
}
return true;
}
//周长
double length() {
double sum = 0.0;
for (double l : ls) sum += l;
return sum;
}
//面积
double area() {
return work.super_s(pionts);
}
// 点在图形里面 包括在图形上
boolean is_in_on(piont piont) {
double sum = 0;
for (int i = 0; i < this.lines.length; i++)
sum += work.super_s(new piont[]{lines[i].x, lines[i].y, piont});
return Math.abs(sum - this.area()) < 1e-6;
}
// 点在图形上面
boolean is_on(piont piont) {
for (line line : lines)
if (line.IsOn(piont))
return true;
return false;
}
// 线段是否参与构造多边形
boolean is_graphic_line(line line) {
for (line line1 : lines)
if (line.IsSame(line1))
return true;
return false;
}
// 点是否在多边形上
boolean is_on_line(piont piont) {
if (this.is_piont(piont))
return true;
else {
for (int i = 0; i < this.lines.length; i++)
if (this.lines[i].IsOn(piont))
return true;
}
return false;
}
//点是否为多边形顶点
boolean is_piont(piont piont) {
for (piont piont1 : pionts)
if (piont1.IsSame(piont))
return true;
return false;
}
//线段是否与多边形有交点
boolean is_banana_by_segment(line line) {
for (line line1 : lines)
if (line1.line_segment_banana(line))
return true;
return false;
}
//线切割
void banana(line line) {
piont[] piontss = new piont[2];
int k = 0;
for (int i = 0; i < lines.length; i++) {
if (!lines[i].IsNotBanana(line)) {
piont tmp = lines[i].Banana(line);
if (!tmp.is_in(piontss, k) && lines[i].IsOn(tmp))
piontss[k++] = tmp;
}
}
if (k == 0) {
System.out.println("0");
return;
}
if (k == 1) {
System.out.println("1");
return;
}
piont[] ups = new piont[pionts.length], downs = new piont[pionts.length], ons = new piont[pionts.length];
int up = 0, down = 0, on = 0;
for (piont p : pionts) {
if (line.Direction(p) == -1)
ups[up++] = p;
if (line.Direction(p) == 0)
ons[on++] = p;
if (line.Direction(p) == 1)
downs[down++] = p;
}
piont[] points = new piont[up + 2];
for (int i = 0; i < up + 2; i++) {
if (i == 0)
points[i] = piontss[0];
else if (i == 1)
points[i] = piontss[1];
else points[i] = ups[i - 2];
}
double s1 = work.super_s(points);
double s2 = this.area() - s1;
if (s1 >= s2) {
System.out.println("2 " + work.Print(s2) + " " + work.Print(s1));
} else
System.out.println("2 " + work.Print(s1) + " " + work.Print(s2));
}
// 多边形相交返回交点组
piont[] banana(graphic graphic) {
piont[] ps = new piont[this.lines.length * graphic.lines.length];
int k = 0;
for (int i = 0; i < this.lines.length; i++)
for (int j = 0; j < graphic.lines.length; j++) {
if (this.lines[i].line_segment_banana(graphic.lines[j]) && !this.lines[i].IsNotBanana(graphic.lines[j])) {
piont p = this.lines[i].Banana(graphic.lines[j]);
if (!p.is_in(ps, k))
ps[k++] = p;
}
}
for (int i = 0; i < this.pionts.length; i++)
if (graphic.is_in_on(pionts[i]))
if (!pionts[i].is_in(ps, k))
ps[k++] = pionts[i];
for (int i = 0; i < graphic.pionts.length; i++)
if (this.is_in_on(graphic.pionts[i]))
if (!graphic.pionts[i].is_in(ps, k))
ps[k++] = graphic.pionts[i];
piont[] pss = new piont[k];
for (int i = 0; i < k; i++)
pss[i] = ps[i];
return pss;
}
// 多边形相交返回交点数目
int banana_point(graphic graphic) {
piont[] ps = new piont[this.lines.length * graphic.lines.length];
int k = 0;
for (int i = 0; i < this.lines.length; i++)
for (int j = 0; j < graphic.lines.length; j++) {
if (this.lines[i].line_segment_banana(graphic.lines[j]) && !this.lines[i].IsNotBanana(graphic.lines[j])) {
piont p = this.lines[i].Banana(graphic.lines[j]);
if (!p.is_in(ps, k))
ps[k++] = p;
}
}
for (int i = 0; i < this.pionts.length; i++)
if (graphic.is_in_on(pionts[i]))
if (!pionts[i].is_in(ps, k))
ps[k++] = pionts[i];
for (int i = 0; i < graphic.pionts.length; i++)
if (this.is_in_on(graphic.pionts[i]))
if (!graphic.pionts[i].is_in(ps, k))
ps[k++] = graphic.pionts[i];
return k;
}
//克隆点组
static piont[] clone_pionts(piont[] ps1) {
int num = 0;
piont[] ps = new piont[ps1.length];
for (piont piont : ps1) {//for(int i=0;i<ps1.length;i++) ps1[i]
ps[num] = new piont();
ps[num++].set(piont.x, piont.y);
}
return ps;
}
//克隆线组
static line[] clone_lines(line[] ps1) {
int num = 0;
line[] ps = new line[ps1.length];
for (line piont : ps1) {
ps[num] = new line();
ps[num++].SetK(piont.x, piont.y);
}
return ps;
}
}思路还是和第一次切割作业相同,都是先判断多边形多个点分别在线的哪一侧,让在同一侧的点与线的交点组成多边形,任何运用多边形类里面的方法,求出相应结果。
7-2 点线形系列5-凸五边形的计算-2
用户输入一组选项和数据,进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
4:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),判断它们两个之间是否存在包含关系(一个多边形有一条或多条边与另一个多边形重合,其他部分都包含在另一个多边形内部,也算包含)。
两者存在六种关系:1、分离(完全无重合点) 2、连接(只有一个点或一条边重合) 3、完全重合 4、被包含(前一个多边形在后一个多边形的内部)5、交错 6、包含(后一个多边形在前一个多边形的内部)。
各种关系的输出格式如下:
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon
5:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),输出两个多边形公共区域的面积。注:只考虑每个多边形被另一个多边形分割成最多两个部分的情况,不考虑一个多边形将另一个分割成超过两个区域的情况。
6:输入六个点坐标,输出第一个是否在后五个点所构成的多边形(限定为凸多边形,不考虑凹多边形),的内部(若是五边形输出in the pentagon/outof the pentagon,若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。输入入错存在冗余点要排除,冗余点的判定方法见选项5。如果点在多边形的某条边上,输出"on the triangle/on the quadrilateral/on the pentagon"。
以上4、5、6选项输入的五个点坐标可能存在冗余,假设多边形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如:x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z不与xy都相邻,如:z x y s、x z s y、x s z y
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
输出的数据若小数点后超过3位,只保留小数点后3位,多余部分采用四舍五入规则进到最低位。小数点后若不足3位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333,1.0按格式输出为1.0
输入样例:
在这里给出一组输入。例如:
4:0,0 6,0 7,1 8,3 6,6 0,0 6,0 7,1 8,3 6,6输出样例:
在这里给出相应的输出。例如:
the previous pentagon coincides with the following pentagon更多样例请查看附件:
点线形系列5-五边形题目详情.pdf
类图
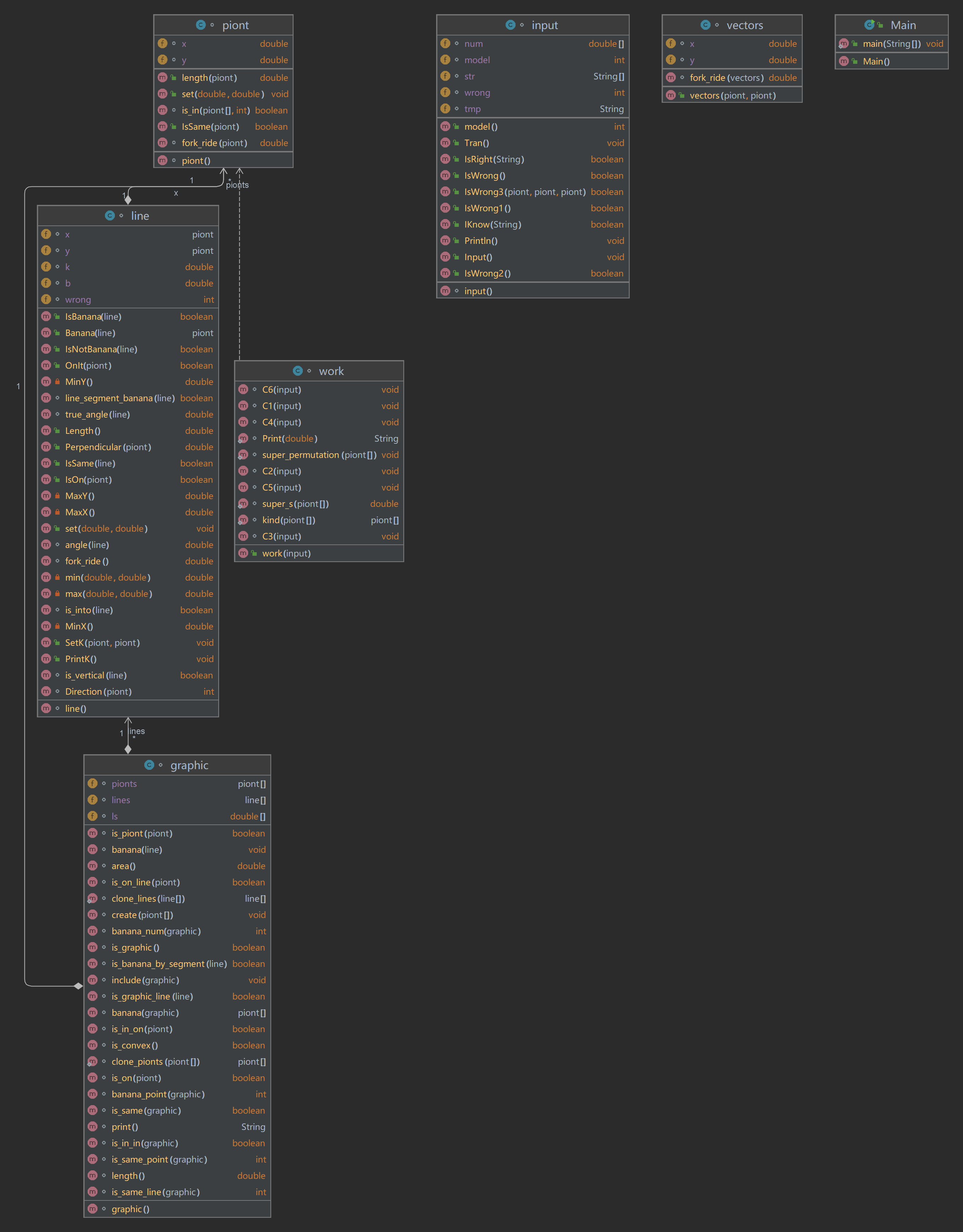
分析代码软件结果

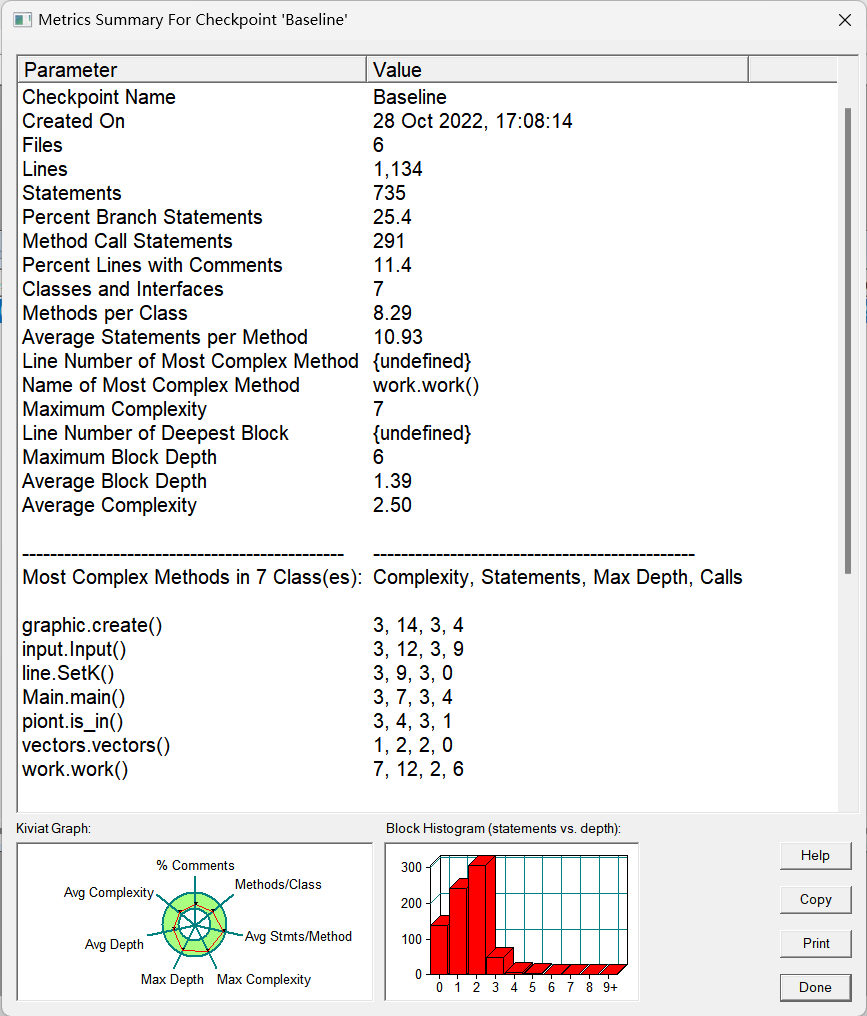
核心代码分析
多边形类
class graphic {
// 所有图形类的父类
piont[] pionts;//顶点集
line[] lines;//线集
double[] ls;//线段长度
void create(piont[] pionts1) {
piont[] pionts = graphic.clone_pionts(pionts1);
this.pionts = pionts;
int num = 0;
line[] lines1 = new line[this.pionts.length];
for (int i = 0; i < pionts.length; i++) {
line line = new line();
line.SetK(pionts[i], pionts[(i + 1) % (pionts.length)]);
lines1[num++] = line;
}
lines = lines1;
int k = 0;
double[] lss = new double[lines.length];
for (line line : lines)
lss[k++] = line.Length();
ls = lss;
}
//判断是否构成多边形
boolean is_graphic() {
if (this.pionts.length == 5) {
piont[] kind = work.kind(this.pionts);
if (kind.length != this.pionts.length)
return false;
}
if (this.lines.length < 3)
return false;
if (this.lines.length == 3) {
line line1 = new line();
line line2 = new line();
line1.SetK(pionts[0], pionts[1]);
line2.SetK(pionts[1], pionts[2]);
return !line1.IsSame(line2);
}
for (int i = 0; i < this.lines.length; i++) {
for (int j = 0; j < this.lines.length; j++) {
if (i != j)
// 非相邻边不相交
if (j != (i + 1) % this.lines.length && j != (i - 1 + this.lines.length) % this.lines.length) {
if (this.lines[i].line_segment_banana(this.lines[j]))
return false;
// 临边不平行
else if (j == (i + 1) % this.lines.length || j == (i - 1 + this.lines.length) % this.lines.length) {
if (this.lines[i].IsNotBanana(this.lines[j]))
return false;
}
}
}
}
return true;
}
//判断是否凸多边形
boolean is_convex() {
piont[] ps = clone_pionts(pionts);
vectors[] vs = new vectors[lines.length];
int k = 0;
for (int i = 0; i < ps.length; i++) {
vectors v = new vectors(ps[i], ps[(i + 1) % ps.length]);
vs[k++] = v;
}
double mult = 0.0;
for (int i = 0; i < k; i++) {
if (mult * vs[i].fork_ride(vs[(i + 1) % vs.length]) < 0)
return false;
mult = vs[i].fork_ride(vs[(i + 1) % vs.length]);
}
return true;
}
//周长
double length() {
double sum = 0.0;
for (double l : ls) sum += l;
return sum;
}
//面积
double area() {
return work.super_s(pionts);
}
// 点在图形里面 包括在图形上
boolean is_in_on(piont piont) {
double sum = 0;
for (int i = 0; i < this.lines.length; i++)
sum += work.super_s(new piont[]{lines[i].x, lines[i].y, piont});
return Math.abs(sum - this.area()) < 1e-6;
}
// 点在图形上面
boolean is_on(piont piont) {
for (line line : lines)
if (line.IsOn(piont))
return true;
return false;
}
// 线段是否参与构造多边形
boolean is_graphic_line(line line) {
for (line line1 : lines)
if (line.IsSame(line1))
return true;
return false;
}
// 点是否在多边形上
boolean is_on_line(piont piont) {
if (this.is_piont(piont))
return true;
else {
for (int i = 0; i < this.lines.length; i++)
if (this.lines[i].IsOn(piont))
return true;
}
return false;
}
//点是否为多边形顶点
boolean is_piont(piont piont) {
for (piont piont1 : pionts)
if (piont1.IsSame(piont))
return true;
return false;
}
//线段是否与多边形有交点
boolean is_banana_by_segment(line line) {
for (line line1 : lines)
if (line1.line_segment_banana(line))
return true;
return false;
}
//返回多边形与多边形的交点个数
int banana_num(graphic graphic) {
int num = 0;
for (line line1 : this.lines)
for (line line2 : graphic.lines)
if (line1.line_segment_banana(line2))
num++;
return num;
}
// 完全重合(点判断)
boolean is_same(graphic graphic) {
int num = 0;
for (piont piont : pionts)
for (piont piont1 : graphic.pionts)
if (piont.IsSame(piont1))
num++;
return num == graphic.pionts.length;
}
//this包含graohic(graphic在this里面)
boolean is_in_in(graphic graphic) {
for (int i = 0; i < graphic.pionts.length; i++) {
if (!this.is_in_on(graphic.pionts[i]))
return false;
}
return true;
}
//返回字符串类型的名字
String print() {
switch (this.pionts.length) {
case 3:
return "triangle";
case 4:
return "quadrilateral";
case 5:
return "pentagon";
}
return null;
}
//返回重合线个数
int is_same_line(graphic graphic) {
int num = 0;
for (line line1 : lines)
for (line line2 : graphic.lines)
if (line1.is_into(line2) || line2.is_into(line1))
num++;
return num;
}
//返回重合点个数
int is_same_point(graphic graphic) {
int num = 0;
for (piont piont : pionts)
for (piont piont1 : graphic.pionts)
if (piont.IsSame(piont1))
num++;
return num;
}
// // 两者存在六种关系:1、分离(完全无重合点) 2、连接(只有一个点或一条边重合) 3、完全重合 4、被包含(前一个多边形在后一个多边形的内部)
//// 5、交错 6、包含(后一个多边形在前一个多边形的内部)。(一个多边形有一条或多条边与另一个多边形重合,其他部分都包含在另一个多边形内部,也算包含)。
void include(graphic graphic) {
int model = 0;
if (this.is_same(graphic)) {
System.out.println("the previous " + print() + " coincides with the following " + graphic.print());//完全重合
return;
} else if (this.is_in_in(graphic)) {//包含(后一个多边形在前一个多边形的内部)。
System.out.println("the previous " + this.print() + " contains the following " + graphic.print());
return;
} else if (graphic.is_in_in(this)) {//被包含(前一个多边形在后一个多边形的内部)
System.out.println("the previous " + this.print() + " is inside the following " + graphic.print());
return;
} else if (this.banana_num(graphic) == 0) {//分离(完全无重合点)
System.out.println("no overlapping area between the previous " + print() + " and the following " + graphic.print());
return;
} else if ((this.is_same_line(graphic) == 1 && this.banana_point(graphic) == 2) || (this.is_same_point(graphic) == 1 && this.banana_point(graphic) == 1)) {//连接(只有一个点或一条边重合)
System.out.println("the previous " + print() + " is connected to the following " + graphic.print());
return;
} else {//交错
System.out.println("the previous " + print() + " is interlaced with the following " + graphic.print());
}
}
//线切割
void banana(line line) {
piont[] piontss = new piont[2];
int k = 0;
for (int i = 0; i < lines.length; i++) {
if (!lines[i].IsNotBanana(line)) {
piont tmp = lines[i].Banana(line);
if (!tmp.is_in(piontss, k) && lines[i].IsOn(tmp))
piontss[k++] = tmp;
}
}
if (k == 0) {
System.out.println("0");
return;
}
if (k == 1) {
System.out.println("1");
return;
}
piont[] ups = new piont[pionts.length], downs = new piont[pionts.length], ons = new piont[pionts.length];
int up = 0, down = 0, on = 0;
for (piont p : pionts) {
if (line.Direction(p) == -1)
ups[up++] = p;
if (line.Direction(p) == 0)
ons[on++] = p;
if (line.Direction(p) == 1)
downs[down++] = p;
}
piont[] points = new piont[up + 2];
for (int i = 0; i < up + 2; i++) {
if (i == 0)
points[i] = piontss[0];
else if (i == 1)
points[i] = piontss[1];
else points[i] = ups[i - 2];
}
double s1 = work.super_s(points);
double s2 = this.area() - s1;
if (s1 >= s2) {
System.out.println("2 " + work.Print(s2) + " " + work.Print(s1));
} else
System.out.println("2 " + work.Print(s1) + " " + work.Print(s2));
}
// 多边形相交返回交点组
piont[] banana(graphic graphic) {
piont[] ps = new piont[this.lines.length * graphic.lines.length];
int k = 0;
for (int i = 0; i < this.lines.length; i++)
for (int j = 0; j < graphic.lines.length; j++) {
if (this.lines[i].line_segment_banana(graphic.lines[j]) && !this.lines[i].IsNotBanana(graphic.lines[j])) {
piont p = this.lines[i].Banana(graphic.lines[j]);
if (!p.is_in(ps, k))
ps[k++] = p;
}
}
for (int i = 0; i < this.pionts.length; i++)
if (graphic.is_in_on(pionts[i]))
if (!pionts[i].is_in(ps, k))
ps[k++] = pionts[i];
for (int i = 0; i < graphic.pionts.length; i++)
if (this.is_in_on(graphic.pionts[i]))
if (!graphic.pionts[i].is_in(ps, k))
ps[k++] = graphic.pionts[i];
piont[] pss = new piont[k];
for (int i = 0; i < k; i++)
pss[i] = ps[i];
return pss;
}
// 多边形相交返回交点数目
int banana_point(graphic graphic) {
piont[] ps = new piont[this.lines.length * graphic.lines.length];
int k = 0;
for (int i = 0; i < this.lines.length; i++)
for (int j = 0; j < graphic.lines.length; j++) {
if (this.lines[i].line_segment_banana(graphic.lines[j]) && !this.lines[i].IsNotBanana(graphic.lines[j])) {
piont p = this.lines[i].Banana(graphic.lines[j]);
if (!p.is_in(ps, k))
ps[k++] = p;
}
}
for (int i = 0; i < this.pionts.length; i++)
if (graphic.is_in_on(pionts[i]))
if (!pionts[i].is_in(ps, k))
ps[k++] = pionts[i];
for (int i = 0; i < graphic.pionts.length; i++)
if (this.is_in_on(graphic.pionts[i]))
if (!graphic.pionts[i].is_in(ps, k))
ps[k++] = graphic.pionts[i];
return k;
}
//克隆点组
static piont[] clone_pionts(piont[] ps1) {
int num = 0;
piont[] ps = new piont[ps1.length];
for (piont piont : ps1) {//for(int i=0;i<ps1.length;i++) ps1[i]
ps[num] = new piont();
ps[num++].set(piont.x, piont.y);
}
return ps;
}
//克隆线组
static line[] clone_lines(line[] ps1) {
int num = 0;
line[] ps = new line[ps1.length];
for (line piont : ps1) {
ps[num] = new line();
ps[num++].SetK(piont.x, piont.y);
}
return ps;
}
}本次作业思路很明了,还是利用之前的成果拼凑出一个图形类,剔除掉了三角形、四边形、五边形类,统一合成图形类,使代码更加易读。
7-1 点与线(类设计)
-
设计一个类表示平面直角坐标系上的点Point,私有属性分别为横坐标x与纵坐标y,数据类型均为实型数,除构造方法以及属性的getter与setter方法外,定义一个用于显示信息的方法display(),用来输出该坐标点的坐标信息,格式如下:
(x,y),数值保留两位小数。为简化题目,其中,坐标点的取值范围设定为(0,200]。若输入有误,系统则直接输出Wrong Format -
设计一个类表示平面直角坐标系上的线Line,私有属性除了标识线段两端的点point1、point2外,还有一个字符串类型的color,用于表示该线段的颜色,同样,除构造方法以及属性的getter与setter方法外,定义一个用于计算该线段长度的方法getDistance(),还有一个用于显示信息的方法display(),用来输出线段的相关信息,输出格式如下:
``` The line's color is:颜色值 The line's begin point's Coordinate is: (x1,y1) The line's end point's Coordinate is: (x2,y2) The line's length is:长度值 ```其中,所有数值均保留两位小数,建议可用
String.format("%.2f", data)方法。设计类图如下图所示。
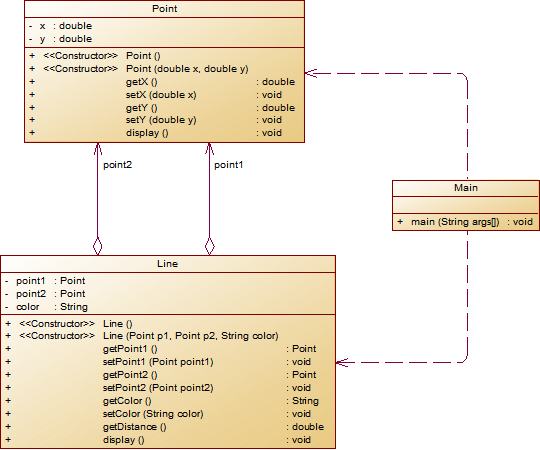
** 题目要求:在主方法中定义一条线段对象,从键盘输入该线段的起点坐标与终点坐标以及颜色,然后调用该线段的display()方法进行输出。**
- 以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭
输入格式:
分别输入线段的起点横坐标、纵坐标、终点的横坐标、纵坐标以及颜色,中间可用一个或多个空格、tab或者回车分隔。
输出格式:
The line's color is:颜色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:长度值输入样例1:
在这里给出一组输入。例如:
5
9.4
12.3
84
Red输出样例1:
在这里给出相应的输出。例如:
The line's color is:Red
The line's begin point's Coordinate is:
(5.00,9.40)
The line's end point's Coordinate is:
(12.30,84.00)
The line's length is:74.96输入样例2:
在这里给出一组输入。例如:
80.2356
352.12
24.5
100
Black输出样例2:
在这里给出相应的输出。例如:
Wrong Format分析
不难。
7-2 点线面问题重构(继承与多态)
在“点与线(类设计)”题目基础上,对题目的类设计进行重构,以实现继承与多态的技术性需求。
- 对题目中的点Point类和线Line类进行进一步抽象,定义一个两个类的共同父类Element(抽象类),将display()方法在该方法中进行声明(抽象方法),将Point类和Line类作为该类的子类。
- 再定义一个Element类的子类面Plane,该类只有一个私有属性颜色color,除了构造方法和属性的getter、setter方法外,display()方法用于输出面的颜色,输出格式如下:
The Plane's color is:颜色 - 在主方法内,定义两个Point(线段的起点和终点)对象、一个Line对象和一个Plane对象,依次从键盘输入两个Point对象的起点、终点坐标和颜色值(Line对象和Plane对象颜色相同),然后定义一个Element类的引用,分别使用该引用调用以上四个对象的display()方法,从而实现多态特性。示例代码如下:
element = p1;//起点Point element.display(); element = p2;//终点Point element.display(); element = line;//线段 element.display(); element = plane;//面 element.display();类结构如下图所示。
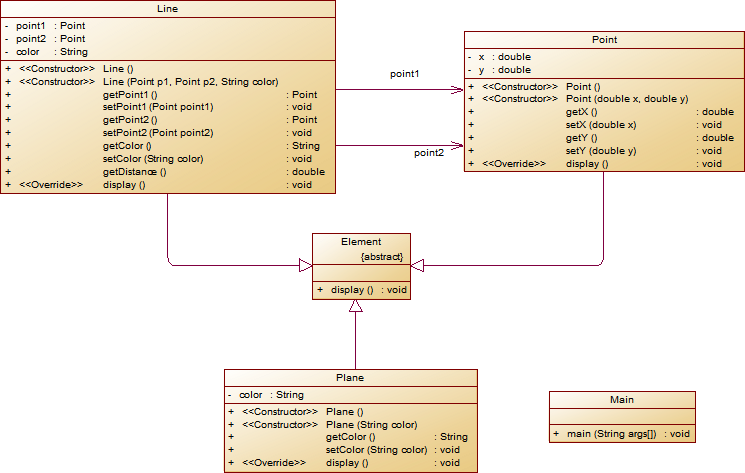
其中,所有数值均保留两位小数,建议可用String.format("%.2f", data)方法。
- 以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭
输入格式:
分别输入线段的起点横坐标、纵坐标、终点的横坐标、纵坐标以及颜色,中间可用一个或多个空格、tab或者回车分隔。
输出格式:
(x1,y1)
(x2,y2)
The line's color is:颜色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:长度值
The Plane's color is:颜色值输入样例1:
在这里给出一组输入。例如:
5
9.4
12.3
84
Red输出样例1:
在这里给出相应的输出。例如:
(5.00,9.40)
(12.30,84.00)
The line's color is:Red
The line's begin point's Coordinate is:
(5.00,9.40)
The line's end point's Coordinate is:
(12.30,84.00)
The line's length is:74.96
The Plane's color is:Red输入样例2:
在这里给出一组输入。例如:
5
9.4
12.3
845
Black输出样例2:
在这里给出相应的输出。例如:
Wrong Format分析
不难
7-3 点线面问题再重构(容器类)
在“点与线(继承与多态)”题目基础上,对题目的类设计进行重构,增加容器类保存点、线、面对象,并对该容器进行相应增、删、遍历操作。
- 在原有类设计的基础上,增加一个GeometryObject容器类,其属性为
ArrayList<Element>类型的对象(若不了解泛型,可以不使用<Element>) - 增加该类的
add()方法及remove(int index)方法,其功能分别为向容器中增加对象及删除第index - 1(ArrayList中index>=0)个对象 - 在主方法中,用户循环输入要进行的操作(choice∈[0,4]),其含义如下:
- 1:向容器中增加Point对象
- 2:向容器中增加Line对象
- 3:向容器中增加Plane对象
- 4:删除容器中第index - 1个数据,若index数据非法,则无视此操作
- 0:输入结束
choice = input.nextInt(); while(choice != 0) { switch(choice) { case 1://insert Point object into list ... break; case 2://insert Line object into list ... break; case 3://insert Plane object into list ... break; case 4://delete index - 1 object from list int index = input.nextInt(); ... } choice = input.nextInt(); }输入结束后,按容器中的对象顺序分别调用每个对象的display()方法进行输出。
类图如下所示:
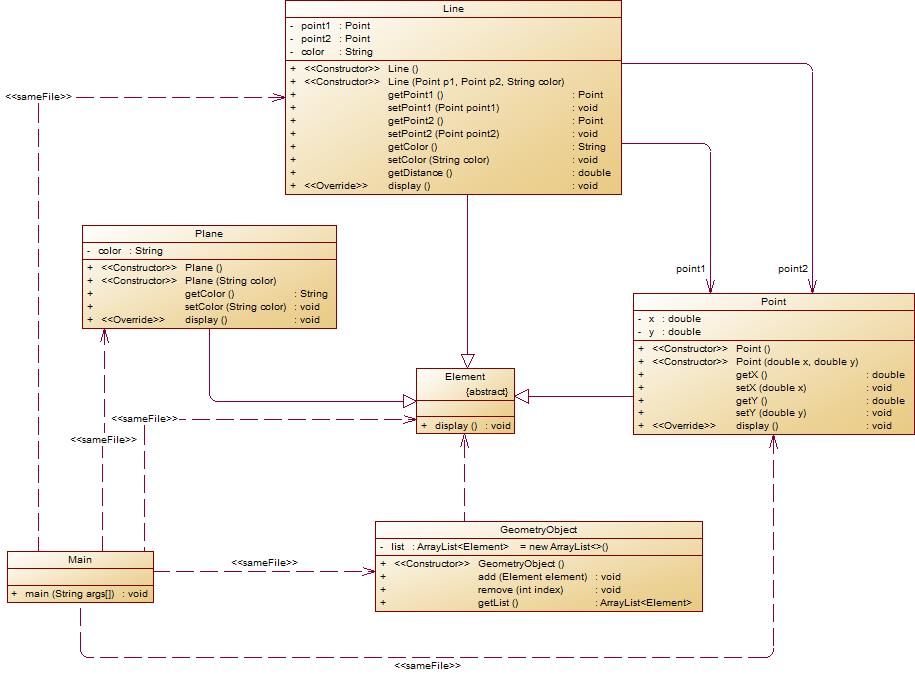
- 以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭
输入格式:
switch(choice) {
case 1://insert Point object into list
输入“点”对象的x,y值
break;
case 2://insert Line object into list
输入“线”对象两个端点的x,y值
break;
case 3://insert Plane object into list
输入“面”对象的颜色值
break;
case 4://delete index - 1 object from list
输入要删除的对象位置(从1开始)
...
}输出格式:
- Point、Line、Plane的输出参考题目2
- 删除对象时,若输入的index超出合法范围,程序自动忽略该操作
输入样例:
在这里给出一组输入。例如:
1
3.4
5.6
2
4.4
8.0
0.98
23.888
Red
3
Black
1
9.8
7.5
3
Green
4
3
0输出样例:
在这里给出相应的输出。例如:
(3.40,5.60)
The line's color is:Red
The line's begin point's Coordinate is:
(4.40,8.00)
The line's end point's Coordinate is:
(0.98,23.89)
The line's length is:16.25
(9.80,7.50)
The Plane's color is:Green分析
代码import java.util.ArrayList;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int choice;
String colour;
GeometryObject geometryObject = new GeometryObject();
for (; ; ) {
choice = sc.nextInt();
if (choice == 0)
break;
switch (choice) {
case 1://insert Point object into list
// 输入“点”对象的x,y值
double x, y;
x = sc.nextDouble();
y = sc.nextDouble();
if (is_in_law(x) && is_in_law(y))
geometryObject.add(new point(x, y));
else return;
break;
case 2://insert Line object into list
// 输入“线”对象两个端点的x,y值
double x1 = sc.nextDouble();
double y1 = sc.nextDouble();
double x2 = sc.nextDouble();
double y2 = sc.nextDouble();
colour = sc.next();
if (is_in_law(x1) && is_in_law(y1) && is_in_law(x2) && is_in_law(y2)) {
point p1 = new point(x1, y1);
point p2 = new point(x2, y2);
geometryObject.add(new line(p1, p2, colour));
} else return;
break;
case 3://insert Plane object into list
// 输入“面”对象的颜色值
colour = sc.next();
geometryObject.add(new plane(colour));
break;
case 4://delete index - 1 object from list
// 输入要删除的对象位置(从1开始)
int index = sc.nextInt();
geometryObject.remove(index);
break;
}
}
for (element element : geometryObject.getList())
element.display();
// x1 = sc.nextDouble();
// y1 = sc.nextDouble();
// x2 = sc.nextDouble();
// y2 = sc.nextDouble();
// colour = sc.next();
// if (is_in_law(x1) && is_in_law(y1) && is_in_law(x2) && is_in_law(y2)) {
// point p1 = new point(x1, y1);
// point p2 = new point(x2, y2);
// line line = new line(p1, p2, colour);
// plane plane = new plane(colour);
// element element;
// element = p1;//起点Point
// element.display();
//
// element = p2;//终点Point
// element.display();
//
// element = line;//线段
// element.display();
//
// element = plane;//面
// element.display();
}
static boolean is_in_law(double num) {
return num > 0 && num <= 200;
}
}
class point extends element {
private double x, y;
double getX() {
return x;
}
double getY() {
return y;
}
void setX(double x) {
this.x = x;
}
void setY(double y) {
this.y = y;
}
public point(double x, double y) {
this.x = x;
this.y = y;
}
public point() {
}
void display() {
System.out.println("(" + String.format("%.2f", getX()) + "," + String.format("%.2f", getY()) + ")");
}
}
class line extends element {
private point p1, p2;
private String color;
public line() {
}
public line(point x, point y, String colour) {
this.p1 = x;
this.p2 = y;
this.color = colour;
}
point getP1() {
return p1;
}
point getP2() {
return p2;
}
String getColor() {
return color;
}
void setP1(point p) {
p1 = p;
}
void setP2(point p) {
p2 = p;
}
void setColor(String colour) {
color = colour;
}
double getDistance() {
return Math.sqrt(Math.pow(p1.getY() - p2.getY(), 2) + Math.pow(p1.getX() - p2.getX(), 2));
}
void display() {
System.out.println("The line's color is:" + color);
System.out.println("The line's begin point's Coordinate is:");
p1.display();
System.out.println("The line's end point's Coordinate is:");
p2.display();
System.out.print("The line's length is:");
System.out.printf("%.2f%n", getDistance());
}
}
abstract class element {
abstract void display();
}
class plane extends element {
private String color;
public plane() {
}
public plane(String colour) {
color = colour;
}
void setColor(String colour) {
color = colour;
}
String getColor() {
return color;
}
void display() {
System.out.println("The Plane's color is:" + getColor());
}
}
class GeometryObject {
private ArrayList<element> list = new ArrayList<>();
public GeometryObject() {
}
void add(element element) {
list.add(element);
}
void remove(int index) {
if (index > this.getList().size() || index < 0)
return;
list.remove(index - 1);
}
ArrayList<element> getList() {
return list;
}
}注意判断非法index。(3个题目就因为这个没有都一遍过。X﹏X)
采坑心得
注意一开始最好合成一个图像类来写,要不写五边形切割的时候会非常麻烦。
因为刚开始的方法和思路非常清晰,所以一路上几乎没有踩什么坑。
注意五边形的那个有6个选项,修改正则表达式的选项判断。 ̄へ ̄
还要鞋带定理要把点排序,推荐用极坐标排序。
改进建议
刚开始就应该合成一个图形类,而不是后来等五边形了才开始合成一个图形类。(*  ̄︿ ̄)
合并后应该及时清理原来的已经没用的代码,增加可读性。
总结:
几次作业极大的提高了本人对面向对象编程的理解,且极大的提高了本人的代码能力。受益匪浅。
<( ̄︶ ̄)↗[GO!]


 浙公网安备 33010602011771号
浙公网安备 33010602011771号