STL小结

\(\mathcal{STL}(\mathcal{Standard\ Template\ Library})\)

---

1. \(queue\) (队列)：

   这是一种先进先出的数据结构。

   主要操作：

   操作	功能
   \(front()\)	返回队尾元素的值
   \(pop()\)	弹出队头元素
   \(push(x)\)	将 \(x\) 压入队尾
   \(empty()\)	如果队列为空,返回 \(true\)
   \(size()\)	返回当前队列内元素个数

   海港 \(\mathcal{OJ}\)

   这道题主要思路是用一个队列维护时间，再用一个队列记录这个人的国籍

   代码：

   #include <queue>
   #include <cstdio>
   using namespace std;
   const int TIME = 86400;
   int n, Countries_, t, k, x, f[ 100005 ];
   queue <int> Time, PeoPle;
   int main () {
       scanf ("%d", &n);
       for (int i = 1; i <= n; i ++) {
           scanf ("%d %d", &t, &k);
           while (k --) {
               Time.push(t);
               scanf ("%d", &x);
               PeoPle.push(x);
               Countries_ += f[ x ] == 0 ? 1 : 0;//当这个人是该国家唯一到达的人时，国家数加加
               f[ x ] ++;
           }
           while (Time.empty() == false and t - Time.front() >= TIME) {//在每艘船到达后，维护队列，将不满足条件的人弹出队列，并判断该国是否有人在24小时内到达
               Time.pop();
               if (-- f[ PeoPle.front() ] == 0) {
                   Countries_ --;
               }
               PeoPle.pop();
           }
           printf ("%d\n", Countries_);
       }
       return 0;
   } 
   

---

2. \(stack(\)栈\()\)：

   在我看来，栈与队列相当于孪生兄弟，但是队列 \(pop()\) 弹出队头元素，先进先出；栈 \(pop()\) 弹出栈顶元素，先进后出
   

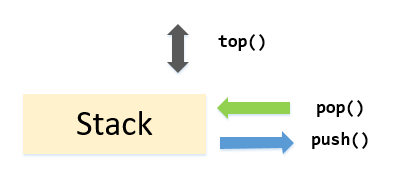
   主要操作：

   操作	功能
   \(top()\)	返回栈顶元素的值
   \(pop()\)	弹出栈顶元素
   \(push(x)\)	将 \(x\) 压入栈顶
   \(empty()\)	如果栈顶元素为空,返回 \(true\)
   \(size()\)	返回当前栈内元素个数

   例题 表达式括号匹配 \(\mathcal{OJ}\)

   思路：如果当前第i位是右括号， 则判断如果前面有左括号且并未用过。若有，将其弹出栈，否则直接输出 \(NO\)
   代码：

   #include <stack>
   #include <cstdio>
   using namespace std;
   stack <char> s;
   int n;
   char c;
   int main () {
   	while (scanf ("%c", &c) != EOF && c != '@') {
   		if (c == '(') {//如果c是左括号，将其push进栈，以便于后面判断
   			s.push(c);
   		}
   		else if (c == ')') {
   			if (s.empty() == true) {//如果栈为空，即前方无可用左括号，则输出"NO"
   				puts("NO");
   				return 0;
   			}
   			s.pop();//若有可用左括号，将左括号弹出，当成已用过
   		}
   	}
   	if (s.empty() == true) {//如果左括号用完，输出"YES"
   		puts("YES");
   		return 0;
   	}
   	puts("NO");
   	return 0;
   } 
   

---

3. \(vector\)(顺序容器,不定长数组)：

   和数组差不多，但比数组优越。特征是相当于可分配拓展的数组。它的随机访问、在末端插入和删除快，但在中间插入和删除慢。

   主要操作：

   操作	功能
   \(push\_back(x)\)	在 \(vector\) 的末尾插入变量 \(x\)
   \(pop\)_\(back()\)	去掉 \(vector\) 的末尾数据
   \(front()\)	返回 \(vector\) 第一个元素
   \(begin()\)	返回 \(vector\) 头的指针
   \(end()\)	返回 \(vector\) 最后一个单元 \(+1\) 的指针
   \(clear()\)	清除 \(vector\) 所有数据
   \(empty()\)	如果 \(vector\) 为空,返回 \(true\)
   \(erase(t)\)	删除t位置的数据
   \(erase(Begin, End)\)	删除 \([Begin, End)\) 区间的数据
   \(size()\)	返回当前\(vector\)中数据个数
   \(insert(t, data)\)	在t处插入数据\(data\)

---

4. \(map\)(关联容器、有序无重复)：

   它提供一对一（其中第一个称为关键字，每个关键字只在 \(map\) 中出现一次，第二个称为该关键字的值）的数据处理能力

   注意：

   1. \(map\) 内部所有的数据都是有序的（红黑树）
   2. 对于迭代器来说，可以修改实值，但不能修改 \(key\)。

   例题 词典 \(\mathcal{OJ}\)

   代码：

   #include <map> 
   #include <cstdio>
   #include <iostream>
   using namespace std;
   map <string, string> Dictionary;
   string s, s2;
   char a[ 155 ], b[ 155 ];
   int main () {
   	while (getline(cin, s, '\n')) {
   		if (s == "") {
   			break;
   		}
   		sscanf(s.c_str(), "%s %s", a, b);
   		Dictionary[ b ] = a;
   	}
   	while (cin >> s) {
   		if (Dictionary[ s ] == "\0") {
   			puts("eh");
   		}
   		else {
   			cout << Dictionary[ s ] << endl;
   		}
   	}
   	return 0;
   }
   

---

5. \(set\)(关联容器,集合)：

   \(set\)是“集合”的意思，\(set\) 中元素都是唯一的，默认情况下会对元素自动进行升序排列，如果需要集合中的元素允许重复那么可以使用 \(multiset\)。

   主要操作：

   操作	功能
   \(begin()\)	返回 \(set\) 中的第一个元素
   \(end()\)	返回 \(set\) 中的最后一个元素
   \(clear()\)	删除 \(set\) 中的所有数据
   \(empty()\)	如果 \(set\) 为空,返回 \(true\)
   \(insert()\)	插入一个元素
   \(erase()\)	删除一个元素
   \(size()\)	返回当前\(set\)中元素个数
   \(count()\)	返回\(set\)中某个值元素的个数
   \(find()\)	返回一个指向被查找到元素的迭代器
   \(lower\_bound()\)	返回指向第一个 \(\geq\) 某个值的元素的迭代器
   \(upper\_bound()\)	返回第一个>某个值的元素的迭代器

   提示：若想让 \(set\) 以降序排序，可使用 \(set<int,\ greater\ < int >\ >\)

---

6. \(priority\_queue\)(优先队列)

   定义：任何时刻，队首元素一定是当前队列中优先级最高（优先值最大）的那一个（大根堆），也可以是最小的那一个（小根堆），可以不断向优先队列中添加某个优先级的元素，也可以不断弹出优先级最高的元素，每次操作会自动调整结构，始终保证队首元素的优先级最高。(懵逼 )

   主要操作：

   操作	功能	时间复杂度
   \(push()\)	将 \(x\) 加入优先队列	\(O(log_2{n}),n\) 为元素个数
   \(pop()\)	队首元素出队	\(O(log_2{n}),n\) 为元素个数
   \(top()\)	获得队首元素	\(O(1)\)
   \(empty()\)	如果优先队列为空,返回 \(true\)	\(O(1)\)
   \(size()\)	返回 \(priority\_queue\) 内元素的个数	\(O(1)\)
   重点：

   \(priority\_queue<int>\ q\ <=>\ priority\_queue<int,\ vector<int>,\ less<int>\ >\ q\) (升序)
   \(priority\_queue<int,\ vector<int>,\ greater<int>\ >\ q\) (降序)

   例题 合并果子 \(\mathcal{OJ}\)

   代码：

   #include <cstdio>
   #include <queue> 
   #include <vector>
   using namespace std;
   priority_queue <int,vector<int>,greater<int> > q;//升序
   int n, a, tot;
   int main () {
       scanf ("%d", &n);
       for (int i = 1; i <= n; i ++) {
           scanf ("%d", &a);
           q.push (a);
       }
       for (int i = 1; i < n; i ++) {//贪心
           int x = q.top ();
           q.pop ();
           x += q.top ();
           q.pop ();
           q.push (x);
           tot += x;
       }
       printf ("%d\n", tot);
       return 0;
   }
   

---