暑假信息培训第一期小结

在七月烈日似火然而太阳未经常露面的重庆，我们进行了二十余天的集训，对二叉树、图论、并查集、数据结构等进行了学习但是一脸懵逼

下面对学习的各种知识进行梳理:

1)\(\mathcal{STL}\)(\(\mathcal{Standard\ Template\ Library}\))

\(queue\)(队列)：

这是一种先进先出的数据结构，主要操作有

操作	功能
\(\mathcal{front()}\)	返回队尾元素的值
\(\mathcal{pop()}\)	弹出队头元素
\(\mathcal{push(x)}\)	将\(x\)压入队尾
\(\mathcal{empty()}\)	如果队列为空,返回\(\mathcal{true}\)
\(\mathcal{size()}\)	返回当前队列内元素个数

例题海港 \(\mathcal{OJ}\)

这道题主要思路是用一个队列维护时间，再用一个队列记录这个人的国籍

代码：

#include <queue>
#include <cstdio>
using namespace std;
const int TIME = 86400;
int n, Countries_, t, k, x, f[ 100005 ];
queue <int> Time, PeoPle;
int main () {
    scanf ("%d", &n);
    for (int i = 1; i <= n; i ++) {
        scanf ("%d %d", &t, &k);
        while (k --) {
            Time.push(t);
            scanf ("%d", &x);
            PeoPle.push(x);
            Countries_ += f[ x ] == 0 ? 1 : 0;//当这个人是该国家唯一到达的人时，国家数加加
            f[ x ] ++;
        }
        while (Time.empty() == false and t - Time.front() >= TIME) {//在每艘船到达后，维护队列，将不满足条件的人弹出队列，并判断该国是否有人在24小时内到达
            Time.pop();
            if (-- f[ PeoPle.front() ] == 0) {
                Countries_ --;
            }
            PeoPle.pop();
        }
        printf ("%d\n", Countries_);
    }
    return 0;
}

\(\mathcal{stack}(\)栈\()\)：

在我看来，栈与队列相当于孪生兄弟，但是队列\(pop()\)弹出队头元素，先进先出；栈\(pop()\)弹出栈顶元素，先进后出

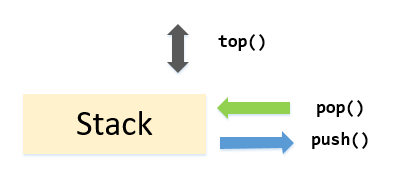
主要操作：

操作	功能
\(\mathcal{top()}\)	返回栈顶元素的值
\(\mathcal{pop()}\)	弹出栈顶元素
\(\mathcal{push(x)}\)	将\(x\)压入栈顶
\(\mathcal{empty()}\)	如果栈顶元素为空,返回\(true\)
\(\mathcal{size()}\)	返回当前栈内元素个数

例题表达式括号匹配 \(\mathcal{OJ}\)

思路：如果当前第i位是右括号，则判断如果前面有左括号且并未用过。若有，将其弹出栈；否则直接输出\(\mathcal{'NO'}\)

重点：要在最后判断左括号是否用完！！！

代码：

#include <stack>
#include <cstdio>
using namespace std;
stack <char> s;
int n;
char c;
int main () {
	while (scanf ("%c", &c) != EOF && c != '@') {
		if (c == '(') {//如果c是左括号，将其push进栈，以便于后面判断
			s.push(c);
		}
		else if (c == ')') {
			if (s.empty() == true) {//如果栈为空，即前方无可用左括号，则输出"NO"
				puts("NO");
				return 0;
			}
			s.pop();//若有可用左括号，将左括号弹出，当成已用过
		}
	}
	if (s.empty() == true) {//如果左括号用完，输出"YES"
		puts("YES");
		return 0;
	}
	puts("NO");
	return 0;
}

\(\mathcal{vector}\)(顺序容器,不定长数组)：

和数组差不多，但比数组优越。特征是相当于可分配拓展的数组。它的随机访问、在末端插入和删除快，但在中间插入和删除慢

主要操作：

操作	功能
\(push\_back(x)\)	在\(vector\)的末尾插入变量\(x\)
\(pop\)_\(back()\)	去掉\(vector\)的末尾数据
\(front()\)	返回\(vector\)第一个元素
\(begin()\)	返回\(vector\)头的指针
\(end()\)	返回\(vector\)最后一个单元\(\ +\ 1\)的指针
\(clear()\)	清除\(vector\)所有数据
\(empty()\)	如果\(vector\)为空,返回\(true\)
\(erase(t)\)	删除t位置的数据
\(\mathcal{erase(Begin, End)}\)	删除\(\mathcal{[Begin, End)}\)区间的数据
\(size()\)	返回当前\(vector\)中数据个数
\(insert(t, data)\)	在t处插入数据\(data\)

\(map\)(关联容器、有序无重复)：

它提供一对一（其中第一个称为关键字，每个关键字只在map中出现一次，第二个称为该关键字的值）的数据处理能力

注意：

\(map\)内部所有的数据都是有序的（红黑树）
对于迭代器来说，可以修改实值，但不能修改\(key\)。

例题词典 \(\mathcal{OJ}\)

代码：

#include <map> 
#include <cstdio>
#include <iostream>
using namespace std;
map <string, string> Dictionary;
string s, s2;
char a[ 155 ], b[ 155 ];
int main () {
	while (getline(cin, s, '\n')) {
		if (s == "") {
			break;
		}
		sscanf(s.c_str(), "%s %s", a, b);
		Dictionary[ b ] = a;
	}
	while (cin >> s) {
		if (Dictionary[ s ] == "\0") {
			puts("eh");
		}
		else {
			cout << Dictionary[ s ] << endl;
		}
	}
	return 0;
}

\(set\)(关联容器,集合)：

\(se\)t是“集合”的意思，\(set\)中元素都是唯一的，默认情况下会对元素自动进行升序排列，如果需要集合中的元素允许重复那么可以使用\(multiset\)。

主要操作：

操作	功能
\(begin()\)	返回\(set\)中的第一个元素
\(end()\)	返回\(set\)中的最后一个元素
\(clear()\)	删除\(set\)中的所有数据
\(empty()\)	如果\(set\)为空,返回\(true\)
\(insert()\)	插入一个元素
\(erase()\)	删除一个元素
\(size()\)	返回当前\(set\)中元素个数
\(count()\)	返回\(set\)中某个值元素的个数
\(find()\)	返回一个指向被查找到元素的迭代器
\(lower\_bound()\)	返回指向第一个\(\geq\) 某个值的元素的迭代器
\(upper\_bound()\)	返回第一个>某个值的元素的迭代器

提示：

若想让\(set\)以降序排序，可使用\(set<int,\ greater\ < int >\ >\)

\(priority\_queue\)(优先队列)

定义：任何时刻，队首元素一定是当前队列中优先级最高（优先值最大）的那一个（大根堆），也可以是最小的那一个（小根堆），可以不断向优先队列中添加某个优先级的元素，也可以不断弹出优先级最高的元素，每次操作会自动调整结构，始终保证队首元素的优先级最高。(懵逼 )

主要操作：

操作	功能	时间复杂度
\(push()\)	将\(x\)加入优先队列	\(\mathcal{O(log_2{n}),n}\)为元素个数
\(pop()\)	队首元素出队	\(\mathcal{O(log_2{n}),n}\)为元素个数
\(top()\)	获得队首元素	\(\mathcal{O(1)}\)
\(empty()\)	如果优先队列为空,返回\(true\)	\(\mathcal{O(1)}\)
\(size()\)	返回\(priority\_queue\)内元素的个数	\(\mathcal{O(1)}\)

重点：

\(\mathcal{priority\_queue<int>\ q\ <=>\ priority\_queue<int,\ vector<int>,\ less<int>\ >\ q}\) (升序)
\(priority\_queue<int,\ vector<int>,\ greater<int>\ >\ q\) (降序)

例题合并果子 \(\mathcal{OJ}\)

代码

#include <cstdio>
#include <queue> 
#include <vector>
using namespace std;
priority_queue <int,vector<int>,greater<int> > q;//升序
int n, a, tot;
int main () {
    scanf ("%d", &n);
    for (int i = 1; i <= n; i ++) {
        scanf ("%d", &a);
        q.push (a);
    }
    for (int i = 1; i < n; i ++) {//贪心
        int x = q.top ();
        q.pop ();
        x += q.top ();
        q.pop ();
        q.push (x);
        tot += x;
    }
    printf ("%d\n", tot);
    return 0;
}

\(\mathcal{STL}\)完结 (手断)

2)可爱又可恨的图论：

术语:

无向图

术语	含义
相邻点	两个顶点之间如果有边连接，那么就视为两个顶点相邻
路径	相邻顶点的序列
圈	起点和终点重合的路径
有向路径	相邻顶点的序列
度	顶点连接的边数
树	没有圈的连通图
森林	没有圈的非连通图

在无向图中，边是双向的，\(\mathcal{So}\)他们的邻接性是双向的。

有向图

术语	含义
出度	以顶点为弧尾的边的数目
入度	以顶点为弧头的边的数目
度	一个顶点的入度与出度之和
有向路径	相邻顶点的序列
有向环	一条至少含有一条边且起点和终点相同的有向路径
有向无环图(\(\mathcal{DAG}\))	没有环的有向图

在有向图中，边是单向的,\(\mathcal{So}\)他们的邻接性是单向的。

存储方式：

邻接矩阵：

说白了，就是一个二维矩阵，看上去简单明了，只是空间复杂度高达n * n（MLE危险）
邻接表：

运用了\(\mathcal{STL}\)当中的\(\mathcal{vector}\)（不定长数组），每次将节点以近似链表的方式接在后方，即使在稀疏图的情况下，也不会有较大的浪费，空间复杂度\(\mathcal{(n + m)}\) (\(\mathcal{LF}\)再也不用担心我\(\mathcal{MLE}\)了)

具体实现：
- 定义一个结构体，在其中放入所需的变量
- 打构造函数 (构造函数应与结构体同名), 为结构体元素赋值

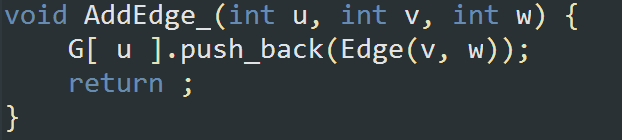
写一个函数\(\mathcal{AddEdge}\)存储信息：

有向图：

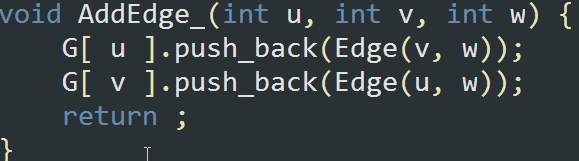
无向图：
输入并调用函数

例题：

模板有向图的\(\mathcal{DFS}\) \(\mathcal{OJ}\)

没什么好说的，一个\(\mathcal{easy}\)的模板，注意顺序！！！

坑点：数据不保证是一个连通图

代码：

#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
int n, m, s, t;
bool f[ 205 ];
vector <int> G[ 205 ];
void DFS(int x) {
	sort (G[ x ].begin(), G[ x ].end());
	for (int i = 0; i < G[ x ].size(); i ++) {
		if (f[ G[ x ][ i ] ] == false) {//如果未遍历过
			printf ("%d ", G[ x ][ i ]);
			f[ G[ x ][ i ] ] = true;//标记为遍历过
			DFS(G[ x ][ i ]);
		}
	}
	return ;
}
int main () {
	scanf ("%d %d", &n, &m);
	for (int i = 1; i <= m; i ++) {
		scanf ("%d %d", &s, &t);
		G[ s ].push_back(t);//有向图
		//无向图加上G[ t ].push_back(s);
	}
	for (int i = 1; i <= n; i ++) {
		if (f[ i ] == false) {
			f[ i ] = true;
			printf ("%d ", i);
		} 
		DFS(i);
	}
	return 0;
}
//快乐AC不用愁

模板有向图的\(\mathcal{BFS}\) \(\mathcal{OJ}\)

为不懂BFS的小盆友们默哀

坑点：数据不保证是一个连通图, \(\mathcal{too}\)

代码：

#include <queue>
#include <vector>
#include <cstdio>
#include <algorithm>
using namespace std;
int n, m, s, t;
bool f[ 205 ];
vector <int> G[ 205 ];
queue <int> q;
void BFS(int x) {//BFS模板
	q.push(x);
	f[ x ] = true;
	while (q.empty() == false) {
		x = q.front();
		printf ("%d ", x);
		q.pop();
		sort(G[ x ].begin(), G[ x ].end());
		for (int i = 0; i < G[ x ].size(); i ++) {
			if (f[ G[ x ][ i ] ] == false) {
				f[ G[ x ][ i ] ] = true;
				q.push(G[ x ][ i ]);
			}
		}
	}
	return ;
}
int main () {
	scanf ("%d %d", &n, &m);
	for (int i = 1; i <= m; i ++) {
		scanf ("%d %d", &s, &t);
		G[ s ].push_back(t);
		//无向图加上G[ t ].push_back(s);
	}
	for (int i = 1; i <= n; i ++) {
		if (f[ i ] == false) {
			BFS(i);
		} 
	}
	return 0;
}
//快乐AC不用愁,too

寻找道路 \(\mathcal{OJ}\)

思路（超纲）现存一个正向图\(\mathcal{G1}\)，再将边反向，存一个反向图\(\mathcal{G2}\)。利用\(\mathcal{G2}\)图从终点开始跑一遍\(\mathcal{BFS}\)，记录这些点能否到达终点。再枚举每一个点，判断这个点是否满足条件，并进行标记。最后运用(超纲知识)\(dijkstra\)跑一遍最短路，最后输出结果，轻松\(\mathcal{AC(138ms)}\)

不懂\(dijkstra\)的小盆友可以点击链接。\(\mathcal{Dijkstra}\)算法图文详解

丑陋的代码：

#include <queue>
#include <cstdio>
#include <vector>
using namespace std;
int n, m, Dis[ 10005 ], x, y, z;
bool f[ 10005 ], f2[ 10005 ];
vector <int> G1[ 10005 ], G2[ 10005 ];
queue <int> Q;
void BFS(int x) {//进行一波预处理（忽略函数名）
	f[ x ] = true;
	Q.push(x);
	while (Q.empty() == false) {
		x = Q.front();
		Q.pop();
		for (int i = 0; i < G1[ x ].size(); i ++) {
			//printf ("%d\n", G1[ x ][ i ]);
			if (f[ G1[ x ][ i ] ] == false) {
				f[ G1[ x ][ i ] ] = true;//标记可以走到终点
				Q.push(G1[ x ][ i ]);//加入队列
			}
		}
	}
	for (int i = 1; i <= n; i ++) {//处理是否符合条件
		for (int j = 0; j < G2[ i ].size(); j ++) {
			if (f[ G2[ i ][ j ] ] == false) {
				//printf ("\n%d %d\n", i, G2[ i ][ j ]);
				f2[ i ] = true;
				break;
			}
		}
		f2[ i ] = f2[ i ] == true ? false : true;
	}
}
void Dijkstra(int s) {//Dijkstra模板
	for (int i = 1; i <= n; i ++) {
		Dis[ i ] = 1e9;
	}
	Dis[ s ] = 0;
	Q.push(s);
	while (Q.empty() == false) {
		int t = Q.front();
		Q.pop();
		for (int i = 0; i < G2[ t ].size(); i ++) {
			if (Dis[ G2[ t ][ i ] ] > Dis[ t ] + 1 and f2[ G2[ t ][ i ] ] == true) {//松弛操作
				Dis[ G2[ t ][ i ] ] = Dis[ t ] + 1;
				Q.push(G2[ t ][ i ]);
			}
		}
	}
	return ;
}
int main() {
//	freopen ("road.in", "r", stdin);
//	freopen ("road.out", "w", stdout);
	scanf ("%d %d", &n, &m);
	while (m --) {
		scanf ("%d %d", &x, &y);
		if (x != y) {//处理自环
			G1[ y ].push_back(x);
			G2[ x ].push_back(y);
		}
	}
	scanf ("%d %d", &x, &y);
	BFS(y);
	Dijkstra(x);
/*	for (int i = 1; i <= n; i ++) {
		printf ("%d ", f2[ i ]);
	}*/
	printf ("%d\n", Dis[ y ] == 1e9 ? -1 : Dis[ y ]);//判断能否走到
	return 0;
}

3) 树(二叉树为主)

概念：

树是\(\mathcal{n（n≥0）}\)个结点的有限集合\(\mathcal{T(Tree)}\)。当\(\mathcal{n=0}\)时，称为空树；当\(\mathcal{n>0}\)时，该集合满足如下条件：
1. 其中必有一个称为根\(\mathcal{（root）}\)的特定结点，它没有直接前驱，但有零个或多个直接后继。
2. 其余n-1个结点可以划分成\(m（m≥0）\)个互不相交的有限集\(\mathcal{T_1，T_2，T_3，…，T_m}\)，其中\(\mathcal{T_i}\)又是一棵树，称为根\(root\)的子树。每棵子树的根结点有且仅有一个直接前驱，但有零个或多个直接后继。
  
  ~~就是一个有n-1条边且没有环的图~~

术语被吃掉了

存储：
1. 顺序存储结构(如图)：

在这里插入图片描述

顺序存储相当于是二叉树的\(\mathcal{BFS}\)序，但要将那些空节点一起放入数组，空间复杂度\(\mathcal{2^{n}}\)(\(n\)为树的最大深度)，容易\(\mathcal{MLE}\)

结构体数组：

这种方法是小编所推崇的。首先定义一个结构体，在其中放入需要的变量(父亲节点、儿子节点、值等)，再定义一个该类型的数组，进行处理

 struct node {
 	int Father, data;
 	vector<int> Children;
 }Tree[ 105 ];
 //多叉树
 struct node {
 	int Father, data, Left_Child, Right_Child;
 }Tree[ 105 ];
 //二叉树

遍历：

先序遍历：

若二叉树为空，则空操作，否则依次执行如下3个操作：

(1) 访问根结点；

(2) 按先序遍历左子树；

(3) 按先序遍历右子树。
中序遍历：

若二叉树为空，则空操作，否则依次执行如下3个操作：

(1) 按先序遍历左子树；

(2) 访问根结点；

(3) 按先序遍历右子树。
后序遍历：

若二叉树为空，则空操作，否则依次执行如下3个操作：

(1) 按先序遍历左子树；

(3) 按先序遍历右子树。

(2) 访问根结点；
BFS序：

每层节点按从左往右的顺序遍历

代码：

void PreOrderTravel(int x) { //先序遍历+输出
	if (x == 0) {
		return ;
	}
	printf ("%d ", x);
	PreOrderTravel(Binary_Tree[ x ].Left_Son);
	PreOrderTravel(Binary_Tree[ x ].Right_Son);
	return ;
}
void InOrderTravel(int x) { //中序遍历+输出
	if (x == 0) {
		return ;
	}
	InOrderTravel(Binary_Tree[ x ].Left_Son);
	printf ("%d ", x);
	InOrderTravel(Binary_Tree[ x ].Right_Son);
	return ;
}
void TailOrderTravel(int x) { //后序遍历+输出
	if (x == 0) {
		return ;
	}
	TailOrderTravel(Binary_Tree[ x ].Left_Son);
	TailOrderTravel(Binary_Tree[ x ].Right_Son);
	printf ("%d ", x);
	return ;
}
void BFS(int Root) { //BFS序+输出
	queue <int> Q;
	Q.push(Root);
	while (Q.empty() == false) {
		int x = Q.front();
		printf ("%d ", x);
		Q.pop();
		if (Binary_Tree[ x ].Left_Son != 0) {
			Q.push(Binary_Tree[ x ].Left_Son);
		}
		if (Binary_Tree[ x ].Right_Son != 0) {
			Q.push(Binary_Tree[ x ].Right_Son);
		}
	}
}

例题：

二叉树遍历 \(\mathcal{OJ}\)

过于\(easy\)，直接上代码：

#include <cstdio>
#include <cstring>
int Len, a[ 105 ];
char s1[ 105 ], s2[ 105 ];
void Tree(int Left,int Right) {
	if (Left > Right) {
		return;
	}
	int Min = 0x3f3f3f3f, Root;
	for (int i = Left; i <= Right; i ++) {
		if (a[ s1[ i ] ] < Min) {
			Min = a[ s1[ i ] ];
			Root = i;
		}
	}
	printf ("%c", s1[ Root ]);
	Tree(Left, Root - 1);
	Tree(Root + 1, Right);
}
int main() {
	scanf("%s %s", s1, s2);
	Len = strlen(s2);
	int i;
	for(i = 0; i < Len; i ++) {
		a[ s2[ i ] ] = i;
	}
	Tree(0, Len - 1);
	return 0;
}

4) 并查集：

定义：如果给出各个元素之间的联系，要求将这些元素分成几个集合，每个集合中的元素直接或间接有联系。在这类问题中主要涉及的是对集合的合并和查找，因此将这种集合称为并查集(就像一棵树)。

三大函数：

\(\mathcal{MakeSet}\)(预处理)：

将每个节点的父亲设为自己(总感觉哪里不大对)
```
void MakeSet(int n) {
	for (int i = 1; i <= n; i ++) {
		Father[ i ] = i;
	}
	return ;
}
```

 2. ### $\mathcal{FindSet}$(找爸爸)：
  	#### 找到该节点的祖先
  	#### 朴素代码：
  	```cpp
  	int FindSet(int x) {
  		while (Father[ x ] != x) {
  			x = Father[ x ];
  		}
  		return x;
  	}
  	```
  	#### $\mathcal{But}$，这样查找过于耗费时间，若变成了一棵退化的树，那么单次查询时间为$\mathcal{O(i)}$，若全部查找一遍，时间复杂度高达$\mathcal{O(n^2)}$，相当于线性表。
  	#### $\mathcal{So}$,路径压缩登场了
  	#### 由于并查集的定义，我们可将这个点的父亲节点接到根节点上，从而降低树的深度，进而将时间复杂度将低。
  	#### 代码：
  	```cpp
  	int FindSet(int x) {
  		if (x != Father[ x ]) {
  			Father[ x ] = FindSet(Father[ x ]);
  		}
  		return Father[ x ];
  	}
  	```

\(\mathcal{UnionSet}\)(合并)

合并两个集合

代码：

void UnionSet(int x, int y) {
	int u = FindSet(x), v = FindSet(y);
	if (u != v) {
		Father[ u ] = v;
	}
}

5) \(\mathcal{DP}\)(动态规划)：

特点：
1. 最优子结构
  
  如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质
2. 无后效性
  
  当前的若干个状态值一旦确定，则此后过程的演变就只和这若干个状态的值有关，和之前是采取哪几个状态演变到当前的这若干个状态，没有关系

解决问题步骤：
1. 状态表示:用一个式子表示划分好的状态
2. 找出答案:找到答案在数组中的下标
3. 状态转移:用子问题的结果得到父亲问题的结果
4. 确定边界:问题初始状态是什么,如何初始化,最小子问题的最优解
神马时候使用\(\mathcal{DP}\)，搜索，贪心，递推：
1. 如果每个阶段都只有一个状态——递推
2. 如果每个阶段的最优解都是由上一个阶段的最优解得到的——贪心
3. 如果每个阶段的最优解是有之前所有的阶段的状态的某种组合得到的——搜索
4. 如果每个阶段的最优解是由之前某个阶段或某些状态直接得到的且不管这些之前的状态是如何得到的——动态规划

经典例题：
1. 简单背包问题 \(\mathcal{OJ}\)
  
  显而易见，爆搜秒秒钟超时。当然，正解有至少两种思路，记忆化搜索与\(\mathcal{DP}\)。接下来，我们就来谈一谈\(\mathcal{DP}\)。
  
  根据经验，这道题是一道明显的完全背包(这还用说吗)。仍然按照解01背包时的思路，令\(\mathcal{DP[ i ][ v ]}\)表示前i种物品恰好放入一个容量为v的背包的最大值。仍然可以按照每种物品不同的策略写出状态转移方程：\(\mathcal{DP[ i ][ v ] = max(DP[ i - 1 ][ v - k * w[ i ] ] + k * c[ i ])\ (0 <= k * w[ i ] <= v)}\)。
  
  \(\mathcal{But,}\)如果我们将01背包内层循环的\(\mathcal{V-0}\)改为\(\mathcal{0-V}\),并运用\(\mathcal{0-1}\)背包转移方程，结果却是对的。\(\mathcal{So}\),我们可以得到转移方程\(\mathcal{DP[ i ][ v ] = max(DP[ i - 1 ][ v - w[ i ] ] + c[ i ])，v从w[ i ]到V}\)
  
  \(\mathcal{Easy}\)的代码(至于输出物品，请开动自己的大脑去理解)：
```
#include <cstdio>
int n, dp[ 45 ][ 45 ], Next[ 45 ][ 1005 ], a[ 45 ], s;
void Print(int x, int y) {
	if (dp[ x ][ y ] == a[ x ]) {
		printf ("%d", a[ x ]);
		return ;
	}
	if (Next[ x ][ y ] == -1) {
		Print(x - 1, y);
	}
	else {
		Print(x - 1, y - a[ x ]);
		printf (" %d", a[ x ]); 
	}
}
int main () {
	scanf ("%d %d", &s, &n);
	for (int i = 1; i <= n; i ++) {
		scanf ("%d", &a[ i ]);
	}
	for (int i = 1; i <= n; i ++) {
		for (int j = s; j >= 1; j --) {
			if (j < a[ i ] or dp[ i - 1 ][ j ] > dp[ i - 1 ][ j - a[ i ] ] + a[ i ]) {
				dp[ i ][ j ] = dp[ i - 1 ][ j ];
				Next[ i ][ j ] = -1;
			}
			else {
				dp[ i ][ j ] = dp[ i - 1 ][ j - a[ i ] ] + a[ i ];
				Next[ i ][ j ] = -2;
			}
		}
	}
	if (s == dp[ n ][ s ]) {
		Print(n, s);
	}
	else {
		puts("Failed!");
	}
	return 0;
}
```

6)分治：

概念：

把一个任务，分为形式和原任务相同，但是规模更小的几个部分任务，分别完成，或只需要选一部分完成。然后再处理完成后的这一个或几部分的结果，实现整个任务的完成。

例题：

模板快速幂 \(\mathcal{OJ}\)

二话不说上代码：

#include <cstdio>
long long Ans_ = 1, t = 2, n;
void qkpow(int n) {
	while (n > 0) {
		if (n % 2 == 1) {
			Ans_ *= t;
		}
		n >>= 1;
		t *= t;
	}
	return ;
}
int main() {
	scanf ("%lld", &n);
	qkpow(n);
	printf ("%lld\n", Ans_);
	return 0;
}

二分法求函数的零点 \(\mathcal{OJ}\)

虽说我曾经硬算出过答案(借助电脑)，但还是来发一波代码吧

#include <cstdio>
bool Check(double x) {
	return x * x * x * x * x - 15 * x * x * x * x + 85 * x * x * x - 225 * x * x + 274 * x - 121 > 0;
}
double Left_ = 1.5, Right_ = 2.4, Mid_;
int main() {
	while(Right_ - Left_ > 0.0000001) {
		Mid_ = (Right_ + Left_) / 2;
		if(Check(Mid_)) {
			Left_ = Mid_;
		}
		else {
			Right_ = Mid_;
		}
	}
	printf("%lf\n", Mid_);
	return 0;
}

好了,分治就讲到这里 (毕竟我也不怎么会)

祝愿各位\(\mathcal{CSP2019.RP++!}\)

完结撒花

\(\mathcal{Update\ 2020.01.12:}\) 修改了一些不能用的链接，美化了字体

posted @ 2020-07-19 22:03 佐世保の时雨酱阅读(244) 评论(1) 收藏举报

刷新页面返回顶部

佐世保の时雨酱

暑假信息培训第一期小结

在七月烈日似火然而太阳未经常露面的重庆，我们进行了二十余天的集训，对二叉树、图论、并查集、数据结构等进行了学习但是一脸懵逼

下面对学习的各种知识进行梳理:

1)\(\mathcal{STL}\)(\(\mathcal{Standard\ Template\ Library}\))

\(queue\)(队列)：

这是一种先进先出的数据结构，主要操作有

例题 海港 \(\mathcal{OJ}\)

这道题主要思路是用一个队列维护时间，再用一个队列记录这个人的国籍

代码：

\(\mathcal{stack}(\)栈\()\)：

在我看来，栈与队列相当于孪生兄弟，但是队列\(pop()\)弹出队头元素，先进先出；栈\(pop()\)弹出栈顶元素，先进后出

主要操作：

例题 表达式括号匹配 \(\mathcal{OJ}\)

思路：如果当前第i位是右括号， 则判断如果前面有左括号且并未用过。若有，将其弹出栈；否则直接输出\(\mathcal{'NO'}\)

重点：要在最后判断左括号是否用完！！！

代码：

\(\mathcal{vector}\)(顺序容器,不定长数组)：

和数组差不多，但比数组优越。特征是相当于可分配拓展的数组。它的随机访问、在末端插入和删除快，但在中间插入和删除慢

主要操作：

\(map\)(关联容器、有序无重复)：

它提供一对一（其中第一个称为关键字，每个关键字只在map中出现一次，第二个称为该关键字的值）的数据处理能力

注意：

\(map\)内部所有的数据都是有序的（红黑树）

对于迭代器来说，可以修改实值，但不能修改\(key\)。

例题 词典 \(\mathcal{OJ}\)

代码：

\(set\)(关联容器,集合)：

\(se\)t是“集合”的意思，\(set\)中元素都是唯一的，默认情况下会对元素自动进行升序排列，如果需要集合中的元素允许重复那么可以使用\(multiset\)。

主要操作：

提示：

若想让\(set\)以降序排序，可使用\(set<int,\ greater\ < int >\ >\)

\(priority\_queue\)(优先队列)

主要操作：

重点：

例题 合并果子 \(\mathcal{OJ}\)

代码

\(\mathcal{STL}\)完结 (手断)

2)可爱又可恨的图论：

术语:

无向图

在无向图中，边是双向的，\(\mathcal{So}\)他们的邻接性是双向的。

有向图

在有向图中，边是单向的,\(\mathcal{So}\)他们的邻接性是单向的。

存储方式：

邻接矩阵：

说白了，就是一个二维矩阵， 看上去简单明了， 只是空间复杂度高达n * n（MLE危险）

邻接表：

运用了\(\mathcal{STL}\)当中的\(\mathcal{vector}\)（不定长数组），每次将节点以近似链表的方式接在后方，即使在稀疏图的情况下，也不会有较大的浪费，空间复杂度\(\mathcal{(n + m)}\) (\(\mathcal{LF}\)再也不用担心我\(\mathcal{MLE}\)了)

具体实现：

定义一个结构体，在其中放入所需的变量

打构造函数 (构造函数应与结构体同名), 为结构体元素赋值

写一个函数\(\mathcal{AddEdge}\)存储信息：

有向图：

无向图：

输入并调用函数

例题：

模板 有向图的\(\mathcal{DFS}\) \(\mathcal{OJ}\)

没什么好说的，一个\(\mathcal{easy}\)的模板，注意顺序！！！

坑点：数据不保证是一个连通图

代码：

模板 有向图的\(\mathcal{BFS}\) \(\mathcal{OJ}\)

为不懂BFS的小盆友们默哀

坑点：数据不保证是一个连通图, \(\mathcal{too}\)

代码：

寻找道路 \(\mathcal{OJ}\)

不懂\(dijkstra\)的小盆友可以点击链接。\(\mathcal{Dijkstra}\)算法图文详解

丑陋的代码：

3) 树(二叉树为主)

概念：

树是\(\mathcal{n（n≥0）}\)个结点的有限集合\(\mathcal{T(Tree)}\)。当\(\mathcal{n=0}\)时，称为空树；当\(\mathcal{n>0}\)时， 该集合满足如下条件：

其中必有一个称为根\(\mathcal{（root）}\)的特定结点，它没有直接前驱，但有零个或多个直接后继。

其余n-1个结点可以划分成\(m（m≥0）\)个互不相交的有限集\(\mathcal{T_1，T_2，T_3，…，T_m}\)，其中\(\mathcal{T_i}\)又是一棵树，称为根\(root\)的子树。 每棵子树的根结点有且仅有一个直接前驱，但有零个或多个直接后继。

就是一个有n-1条边且没有环的图

术语 被吃掉了

存储：

顺序存储结构(如图)：

顺序存储相当于是二叉树的\(\mathcal{BFS}\)序，但要将那些空节点一起放入数组，空间复杂度\(\mathcal{2^{n}}\)(\(n\)为树的最大深度)，容易\(\mathcal{MLE}\)

结构体数组：

这种方法是小编所推崇的。首先定义一个结构体，在其中放入需要的变量(父亲节点、儿子节点、值等)，再定义一个该类型的数组，进行处理

例题海港 \(\mathcal{OJ}\)

例题表达式括号匹配 \(\mathcal{OJ}\)

思路：如果当前第i位是右括号，则判断如果前面有左括号且并未用过。若有，将其弹出栈；否则直接输出\(\mathcal{'NO'}\)

例题词典 \(\mathcal{OJ}\)

例题合并果子 \(\mathcal{OJ}\)

说白了，就是一个二维矩阵，看上去简单明了，只是空间复杂度高达n * n（MLE危险）

模板有向图的\(\mathcal{DFS}\) \(\mathcal{OJ}\)

模板有向图的\(\mathcal{BFS}\) \(\mathcal{OJ}\)

树是\(\mathcal{n（n≥0）}\)个结点的有限集合\(\mathcal{T(Tree)}\)。当\(\mathcal{n=0}\)时，称为空树；当\(\mathcal{n>0}\)时，该集合满足如下条件：

其余n-1个结点可以划分成\(m（m≥0）\)个互不相交的有限集\(\mathcal{T_1，T_2，T_3，…，T_m}\)，其中\(\mathcal{T_i}\)又是一棵树，称为根\(root\)的子树。每棵子树的根结点有且仅有一个直接前驱，但有零个或多个直接后继。

术语被吃掉了

模板快速幂 \(\mathcal{OJ}\)

\(\mathcal{Update\ 2020.01.12:}\) 修改了一些不能用的链接，美化了字体