二叉搜索树（BST）

① 为什么要有二叉搜索树？

当我们用有序数组查找元素时，使用二分查找，复杂度是 O(log n) 的。

当我们在其中插入元素或删除时，复杂度是 O(n) 的。

针对这个问题，就有了二叉搜索树的存在。

② 什么是二叉搜索树？

首先明确二叉搜索树存在的目的：以 O(log n) 的复杂度高效地维护查找、插入、删除的操作。

二叉搜索树的特点：对于任意节点，左子树 < 根节点 < 右子树。

通俗的讲，对于每个节点，其左子树的任意一个节点均小于该节点，其右子树的任意一个节点均大于该节点。

不难发现，二叉搜索树存在的三点性质：

1. 对于具有这样特点的树进行中序遍历，得出的序列必然是有序的。因为，中序遍历就是按照左子树、根、右子树的顺序依次进行的。
2. 二叉搜索树的左右子树均是二叉搜索树。
3. 二叉搜索树的最小值为其左链的顶点，最大值为其右链的顶点。

特殊地，空树是二叉搜索树。

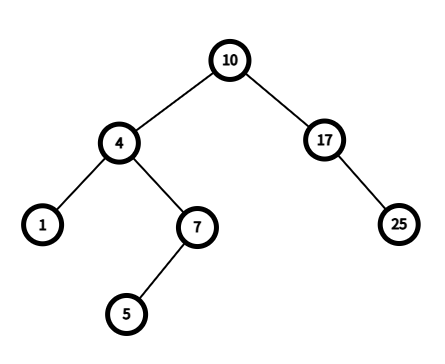
下图是一个典型的二叉搜素树：



class BST {
    public:
    ll key;
    BST* ls, rs;
    BST (ll v) {
        : key (v), ls (nullptr), rs (nullptr) {}
    }
};
// 遍历操作
void inor (BST* u) {
    if (u == nullptr) {
        return;
    }
    inor (u -> ls);
    printf ("%lld", u -> key);
    inor (u -> rs);
}
// 最值查询操作
ll find_min (BST* u) {
    if (u == nullptr) {
        return -1;
    }
    while (u -> ls != nullptr) {
        u = u -> ls;
    } 
    return u -> key;
}
ll find_max (BST* u) {
    if (u == nullptr) {
        return -1;
    }
    while (u -> rs != nullptr) {
        u = u -> rs;
    } 
    return u -> key;   
}

③二叉搜索树的查找

根据二叉搜索树的性质和特点，不难得到以下操作：

从根节点开始查找元素 x，与当前节点对比，（令当前节点元素为 v）若 x < v，在其左子树继续查找；若 x > v 在其右子树继续查找。

重复上述操作，直至找到 x 或查询到叶子节点（即没有元素 x）。

在搜索树均衡的情况下，查找操作的复杂度是 O (log n) 的。

bool search (BST* u, ll x) {
    if (u == nullptr) {
        return false;
    }
    if (u -> key == x) {
        return true;
    } else if (x < u -> key) {
        return search (u -> ls, x);
    } else {
        return search (u -> rs, x);
    }
}

④二叉搜索树的插入

以 u 为根节点的二叉搜索树中插入一个值为 x 的节点。

分类讨论：

若 u 为空， 直接新增节点。

（令 u 的值为 v）若 v > x，在 u 的左子树中继续执行插入操作。

（令 u 的值为 v）若 v < x，在 u 的右子树中继续执行插入操作。

此处不考虑有重复元素的情况。

在搜索树均衡的情况下，查找操作的复杂度是 O (log n) 的。

BST* insert (BST* u, ll v) {
    if (u == nullptr) {
        return new BST (v);
    }
    if (v < u -> key) {
        u -> ls = insert (u -> ls, v);
    } else if (v > u -> key) {
        u -> rs = insert (u -> rs, v);
    }
    return u;
}

⑤二叉搜索树的删除

以 u 为根节点的二叉搜索树中插入一个值为 x 的节点。

令 u 的值为 v，分类讨论：

若 u 为叶子节点，直接删除该节点。

若 u 为链节点，即只有一个儿子的节点，返回这个儿子。

若 u 有两个非空子节点，用其左子树的最大值（即做最靠右的节点）或右子树的最小值（即做最靠左的节点）。

对于第 3 个情况稍加解释，根据二叉搜索树的第 1 条性质：对于具有这样特点的树进行中序遍历，得出的序列必然是有序的。我们不难得到这个序列，而第 3 种情况就是找到该节点在这个序列中的 直接前驱（前者） 或 直接后继（后者）

BST* remove (BST* u, ll v) {
    if (u == nullptr) {
        return u;
    }
    if (v < u -> key) {
        u -> ls = remove (u -> ls, v);
    } else if (v > u -> key) {
        u -> rs = remove (u -> rs, v);
    } else {
        if (u -> ls == nullptr) {
            BST* tmp = u -> rs;
            delete u;
            return tmp;
        } else if (u -> rs == nullptr) {
             BST* tmp = u -> rs;
            delete u;
            return tmp;           
        } else {
            BST* s = find_min (u -> rs);
            u -> key = s -> key;
               u -> rs = remove (u -> rs, s -> key);
        }
    }
    return u;
}