线性代数 矩阵消元

以下是本次我们要讨论的方程组例题：

\( \begin{cases} \,\,\,x+2y+z=2\\ 3x+8y+z=12\\ \,\,\,\,\,\,\,\,\,\,\,\,\,4y+z=2 \end{cases} \,\,\,\,\,\,\,\,\,\,A = \begin{bmatrix} 1&2&1\\ 3&8&1\\ 0&4&1\\ \end{bmatrix} \)

如果消元法奏效，方程的根就出来了。一般来说，消元法是可以解出来的，只要方程组的矩阵 \(A\) 是一个好矩阵，比如上面这个。

对于好矩阵可以粗略理解为非奇异且可逆（总之就是具有一切美好的性质

实际上，对于消元的概念，大家很容易想到。话说高斯先想到这个概念可能是因为他出生早，emm \(\dots\) 当然他逝得也早，消元概念其实很自然（

了解了消元概念以后，我将要做的是用矩阵语言描述消元法。毕竟对于整一个章节来说，核心概念是“矩阵变换”。

好好好，现在我们来看这个方程：三个方程三个未知数，然后是 \(3\times3\) 的矩阵 \(A\) , 方程组表示为 \(A\)X \(=b\) 。

话说在消元的时候大部分时间都是快乐的，不过呢在方程里不断重复加号和等号会很痛苦，所以我会用矩阵表示，这些都能表示为矩阵。

先不管矩阵，回想一下在幼儿园的时候我们是怎么完成消元的？第一步怎么做？我们使第一个方程成立，用该方程乘以某个数，然后从方程二中将它减去，目的是抵消掉里面的一个未知数从而简化方程。

很显然，重点是我们乘以一个什么数可以达到目的，这里的目的是抵消方程二中的 \(x\) ,这里还是用矩阵运算，矩阵更加简洁。

方程一乘以多然后用方程二减去？首先，这个 \(1\) 是消元的关键，它被称为主元。我让第一行不变因为它是主元行，但我将使用它，那么消元乘数取多少？很显然是 \(3\) ， \(1\times3=3\) 可以消掉下面的 \(3x\)。

于是 \(\dots\)

\[\begin{bmatrix} 1&2&1\\ 3&8&1\\ 0&4&1\\ \end{bmatrix} \rightarrow \begin{bmatrix} 1&2&1\\ 0&2&-2\\ 0&4&1\\ \end{bmatrix} \]

有人可能会问：那右侧向量呢？是不是也应该放在后面？实际上 \(MatLab\) 是先算完左侧矩阵，再回头算右侧向量的。

Ok,言归正传。下一步消元是什么？严格来说这里消元的位置应该是 \((2,1)\) 即行二列一，然后用 \((3,1)\) 去抵消成 \(0\)，但是我们已经有 \(0\) 了，所以取 \(0\) 个方程减下来就可以了。

接下来我们继续消元，第二个主元在 \((2,2)\) 的位置，消元乘数是多少？很显然是 \(2\) 很容易理解理解不了的话还是 退役吧 。

\[\begin{bmatrix} 1&2&1\\ 0&2&-2\\ 0&4&1\\ \end{bmatrix} \rightarrow \begin{bmatrix} 1&2&1\\ 0&2&-2\\ 0&0&5\\ \end{bmatrix} \]

好的，我们来还原一下整个变换过程：

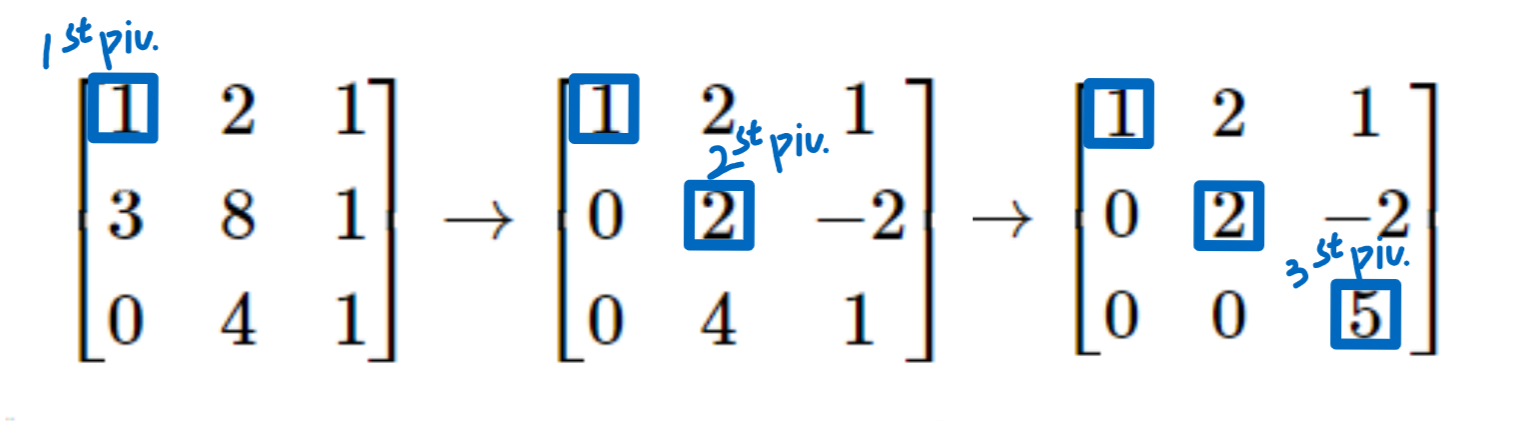
从矩阵 \(A\) 通过消元得到的矩阵记作 \(U\) , \(U\) 表示上三角矩阵，\(U=\begin{bmatrix} 1&2&1\\ 0&2&-2\\ 0&0&5\\ \end{bmatrix}\) 。

因此，这里的消元目的是从 \(A\) 得到 \(U\) ，毫不夸张，这是计算科学中最普遍的运算。顺便提一下，主元不能为 \(0\) 。

好好好，接下来我们讨论一下消元法失效的情况，失效指的是不能得到三个主元。

话说如果第一个数是 \(0\) , \(A = \begin{bmatrix} 0&2&1\\ 3&8&1\\ 0&4&1\\ \end{bmatrix}\) 就已经陷入麻烦，方程就是 \(\begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,2y+z=2\\ 3x+8y+z=12\\ \,\,\,\,\,\,\,\,\,\,\,\,\,4y+z=2 \end{cases}\)

这难道意味着我无法解方程？显然不是。怎么办？行交换即可。这很好理解。不理解的评论问我就行（虽然可能没人会看这篇文章。

然后我突然意识到一个问题，交换行只可以解决主元为 \(0\) 的 “暂时性失效” ，但如果它不暂时的话就麻烦了，比如说：

\(A = \begin{bmatrix} 0&2&1\\ 3&8&1\\ 0&4&-4\\ \end{bmatrix}\) 方程是 \(\begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,2y+\,\,z=2\\ 3x+8y+\,\,z=12\\ \,\,\,\,\,\,\,\,\,\,\,\,\,4y-4z=2 \end{cases}\)

这样就会造成无法摆脱的麻烦，我指的是主元三为 \(0\) ，最后一个主元为 \(0\) 就没地方换了，算到这里就可以确定消元法失效了。所以说，没有方法是万能的。

好，接下来还是讨论回消元法有效的情况。下一个主题是 “回代” 。

什么是“回代”？现在就得把右侧向量带入了。

\(MatLab\) 会怎么做呢？我们照着他来就行了。我们引入右侧向量作为新的一列 \(b=\begin{bmatrix} 2\\12\\2 \end{bmatrix}\) 。

有：

\[\begin{bmatrix} 1&2&1&2\\ 3&8&1&12\\ 0&4&-4&2 \end{bmatrix}\]

我将把他称为 “增广矩阵（\(Augmented\,Matrix\)）”,可以想象，对方程进行消元的时候，右侧向量也会随之变化。

接着，我们按照之前的方式对新的矩阵进行消元：

\[\begin{bmatrix} 1&2&1&2\\ 3&8&1&12\\ 0&4&-4&2 \end{bmatrix} \rightarrow \begin{bmatrix} 1&2&1&2\\ 0&2&-2&6\\ 0&4&1&2\\ \end{bmatrix} \rightarrow \begin{bmatrix} 1&2&1&2\\ 0&2&-2&6\\ 0&0&5&-10\\ \end{bmatrix} \]

那么,我最终得到的右侧向量, 即 \(U\) 对应的 \(b\) 为 \(\begin{bmatrix} 2\\6\\-10 \end{bmatrix}\) 。我们将它记作 \(c\) ，这是固定记号。所以 \(c\) 是 \(b\) 的最终结果，就像 \(U\) 对于 \(A\) 样。

所以，所谓的“回代”就是指将右侧向量带回原方程，有：

\[\begin{cases} x+2y+z=2\\ \,\,\,\,\,\,\,\,\,\,2y-2z=6\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,5z=-10 \end{cases} \]

这就是矩阵 \(U\) 和 \(c\) 的方程含义，也就是 \(U\)X\(=c\) 。最后，方程解得 \( \begin{cases} x=2\\y=1\\z=-2 \end{cases} \) 。

所以你会发现“回代”就是一个很简单的东西，他是反向求解方程的简单步骤。

好的，现在讷我需要铺垫一点东西：

当我们进行矩阵变换的时候，我们可以看到大图。上一章，再讲矩阵乘以右侧向量的时候，我提到过大图。

我们随便假设一个矩阵：

\[\begin{bmatrix} \dots&\dots&\dots\\ \dots&\dots&\dots\\ \dots&\dots&\dots\\ \end{bmatrix} \begin{bmatrix} 3\\4\\5 \end{bmatrix} = \begin{bmatrix} 3 \times col_1\\+\\4 \times col_2\\+\\5 \times col_3 \end{bmatrix} \]

我记得在上一章的时候，我建议大家在计算的时候用列计算。而接下来的计算用的不是列，而是行，为什么？因为这一集的文章讲的都是行变换。因此，上述列的形式是现在不需要的。所以接下来讲一下行表示法。

我还是假设一下我挚爱的矩阵：

\[\begin{bmatrix} 1&2&7 \end{bmatrix} \begin{bmatrix} \dots&\dots&\dots\\ \dots&\dots&\dots\\ \dots&\dots&\dots\\ \end{bmatrix} \]

如图，这是一个 \(1 \times 3\) 的矩阵乘上 \(3 \times 3\) 的矩阵，结果是什么？矩阵乘以一列等于一列，但在这里我用一行乘以一个矩阵应该是这样：

\[\begin{bmatrix} 1&2&7 \end{bmatrix} \begin{bmatrix} \dots&\dots&\dots\\ \dots&\dots&\dots\\ \dots&\dots&\dots\\ \end{bmatrix} = \begin{bmatrix} 1 \times row_1\\+\\2 \times row_2\\+\\3 \times row_3 \end{bmatrix} \]

接下来进入第二部分。

在第二部分中，我们将引入矩阵。

现在我要引入消元矩阵的概念。

从第一步开始，取矩阵：

\[\begin{bmatrix} 1&2&1\\ 3&8&1\\ 0&4&1\\ \end{bmatrix} \]

我的问题是，第一步需要一个什么矩阵？需要一个从第二行中减去三倍的行一，其他行不变。

\[\begin{bmatrix} \dots&\dots&\dots\\ \dots&\dots&\dots\\ \dots&\dots&\dots\\ \end{bmatrix} \begin{bmatrix} 1&2&1\\ 3&8&1\\ 0&4&1\\ \end{bmatrix} = \begin{bmatrix} 1&2&1\\ 0&2&-2\\ 0&4&1\\ \end{bmatrix} \]

好的先在就问未知的矩阵长什么样。很显然，第一行是 \([1,0,0]\)

\[\begin{bmatrix} 1&0&0\\ \dots&\dots&\dots\\ \dots&\dots&\dots\\ \end{bmatrix} \begin{bmatrix} 1&2&1\\ 3&8&1\\ 0&4&1\\ \end{bmatrix} = \begin{bmatrix} 1&2&1\\ 0&2&-2\\ 0&4&1\\ \end{bmatrix} \]

那最后一行是什么？我们只需要 \(1\) 个第 \(3\) 行，于是 \(\dots\)

\[\begin{bmatrix} 1&0&0\\ \dots&\dots&\dots\\ 0&0&1\\ \end{bmatrix} \begin{bmatrix} 1&2&1\\ 3&8&1\\ 0&4&1\\ \end{bmatrix} = \begin{bmatrix} 1&2&1\\ 0&2&-2\\ 0&4&1\\ \end{bmatrix} \]

这里提一个概念叫 “单位矩阵” ，用上面这个例子，如果第二行是 \([0,1,0]\) 的话 \(\dots\)

\[\begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1\\ \end{bmatrix} \begin{bmatrix} 1&2&1\\ 3&8&1\\ 0&4&1\\ \end{bmatrix} = \begin{bmatrix} 1&2&1\\ 3&8&1\\ 0&4&1\\ \end{bmatrix} \]

很显然，乘了就和没乘一样，这个矩阵 \(\begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1\\ \end{bmatrix}\) 就相当于数字 \(1\) 一样，它叫做 “单位矩阵”。那我们简单做一个推广：

如果这是一个 \(n \times n\) 的矩阵，那他的单位矩阵是什么？很显然是对角线是 \(1\) 其他地方是 \(0\) 的矩阵。

长这样:

\[\begin{bmatrix} 1&0&\dots&0\\ 0&1&\dots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&\dots&0&1 \end{bmatrix}\]

好好好，能看懂就行。我们继续上面的话题。

我们这里并不是要让他不改变，那怎样才能得出正确的结果？

很显然 \(\dots\)

\[\begin{bmatrix} 1&0&0\\ -3&1&0\\ 0&0&1\\ \end{bmatrix} \begin{bmatrix} 1&2&1\\ 3&8&1\\ 0&4&1\\ \end{bmatrix} = \begin{bmatrix} 1&2&1\\ 0&2&-2\\ 0&4&1\\ \end{bmatrix} \]

这样就解决了。这样的矩阵相当于三倍的第一行加上一倍的第二行加上零个第三行——这不就是我们想要的吗？

你很容易发现这里的矩阵形式很简单，求矩阵乘法也很顺心，所以它被称作“初等矩阵”，记作 \(E\) 。

\(E_{2,1}\) 表示在位置 \((2,1)\) 上的变换，有\(E_{2,1}=\begin{bmatrix} 1&0&0\\ -3&1&0\\ 0&0&1\\ \end{bmatrix}\)，而接下来我需要用矩阵语言来描述整一个消元的过程。

接下来第二步是什么？用第三行减去两倍的第二行，同样的，什么矩阵能达到目的？

同样的：

\[\begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&-2&1\\ \end{bmatrix} \begin{bmatrix} 1&2&1\\ 0&2&-2\\ 0&4&1\\ \end{bmatrix} = \begin{bmatrix} 1&2&1\\ 0&2&-2\\ 0&0&5\\ \end{bmatrix} \]

好，因为要修正的位置是 \((3,2)\) ，所以 \(E_{3,2}=\begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&-2&1\\ \end{bmatrix}\) 。

OKey，我来简单总结一下我们目前为止干了些什么：

\[E_{3,2}(E_{2,1}A)=U \]

所以现在知道我为什么喜欢矩阵了，它很简洁，放到网上也可以节省空间（

好接下来我要讲一些矩阵的重要性质：

假设我有矩阵 \(A\) 想要得到矩阵 \(U\) ，什么矩阵可以一次性做到？

这个答案很简单，但是非常重要。

\[(E_{3,2}·E_{2,1})A=U \]

先把这些 \(E\) 乘起来。这就是矩阵有乘法结合律。

既然讲到了初等矩阵，那就来看看另一类初等矩阵——“置换矩阵”，话说就是交换行的矩阵。

我举一个置换矩阵的例子：

行交换

（交换第一行和第二行）

\[\begin{bmatrix} 0&1\\1&0 \end{bmatrix} \begin{bmatrix} a&b\\ c&d\\ \end{bmatrix} = \begin{bmatrix} c&d\\a&b \end{bmatrix} \]

\(\begin{bmatrix} 0&1\\1&0 \end{bmatrix}\) 这种矩阵被称为 \(P\) 。

列交换

\[\begin{bmatrix} a&b\\ c&d\\ \end{bmatrix} \begin{bmatrix} 0&1\\1&0 \end{bmatrix} = \begin{bmatrix} b&a\\d&c \end{bmatrix} \]

一定要注意，列变换的时候矩阵右乘。至于为什么左变换的时候左乘而右变换相反可以自行体会，很容易理解。

我们还是讨论回行变换，但是要强调的一点是两个矩阵 \(A\) 和 \(B\)，\(A \times B \neq B \times A\) 。

回到：

\[E_{3,2}(E_{2,1}A)=U \]

我们把矩阵 \(E_{3,2}\) 和 \(E_{2,1}\) 相乘就可以得到致命一击的消元矩阵，但这个你们可以自己去做，不过多讲解，因为那是非常好理解的。

OKey，话说我不讲的原因是还有更好的方法。这个方法不是关于如何从 \(A\) 变成 \(U\) ,而是如何从 \(U\) 变回 \(A\) 。所以，下面进行逆变换。这里用到了“逆”，这就是了解逆矩阵的第一步。

至今为止，提到的所有矩阵都是可逆的。接下来，我先讲一下可逆的含义。

我举个例子：

就拿这个 \(E_{2,1}=\begin{bmatrix} 1&0&0\\ -3&1&0\\ 0&0&1\\ \end{bmatrix}\) 来说。

我们一开始是通过这个矩阵乘上系数矩阵来达到消元的目的：

\[\begin{bmatrix} 1&0&0\\ -3&1&0\\ 0&0&1\\ \end{bmatrix} \begin{bmatrix} 1&2&1\\ 3&8&1\\ 0&4&1\\ \end{bmatrix} = \begin{bmatrix} 1&2&1\\ 0&2&-2\\ 0&4&1\\ \end{bmatrix} \]

而现在我想取消这次消元应该拿什么样的矩阵去乘可以达到目的？这是问题的关键。

很显然（emm\(\dots\)也许不显然），

\[\begin{bmatrix} 1&0&0\\ 3&1&0\\ 0&0&1\\ \end{bmatrix} \begin{bmatrix} 1&0&0\\ -3&1&0\\ 0&0&1\\ \end{bmatrix} = \begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1\\ \end{bmatrix} \]

而矩阵 \(\begin{bmatrix} 1&0&0\\ 3&1&0\\ 0&0&1\\ \end{bmatrix}\) 就是它的逆矩阵，也就是说这个矩阵乘以它可以得到单位矩阵。

如果矩阵\(\begin{bmatrix} 1&0&0\\ -3&1&0\\ 0&0&1\\ \end{bmatrix}\)记作 \(E\) ，矩阵 \(\begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1\\ \end{bmatrix}\) 记作 \(I\) ,则矩阵 \(\begin{bmatrix} 1&0&0\\ 3&1&0\\ 0&0&1\\ \end{bmatrix}\) 记作 \(E^{-1}\) ，即 \(E\) 的逆元，至少你可以这样理解。

本章内容到此结束。

预告：下一章将 \(A\) 的 \(LU\) 分解展开分析。