线性代数 方程组的几何解释

本次，我们将讲述线性代数的基础 —— 求线性方程组，下面从方程组讲起，它有 \(n\) 个未知数以及 \(n\) 个方程，方程数量与未知数个数相等，这是最普遍的状况。

我们会了解到 “行图像（\(RowPictrue\))” 和 “列图像（\(ColumnsPictrue\)）”，行图像想必大家都见过就是两个方程的函数图像交于一点的形式，而列图像大家可能是第一次见到。

接下来，以此方程为例：

\[\begin{cases} 2x\,-y=0 \\ -x+2y=3 \end{cases} \]

现在立马就有矩阵的概念了，准确来说应该是方程的系数矩阵。

\[ \begin{bmatrix} -2&-1\\ -1&-2\\ \end{bmatrix} \begin{bmatrix} x\\y \end{bmatrix} = \begin{bmatrix} 0\\3 \end{bmatrix} \]

一般来说，我们会用字母 \(A\) , X 和 \(b\) 来给上面 \(3\) 的矩阵命名。

\[A=\begin{bmatrix} -2&-1\\ -1&-2\\ \end{bmatrix} ,X=\begin{bmatrix} x\\y \end{bmatrix} ,b=\begin{bmatrix} 0\\3 \end{bmatrix} \]

\(A\) 是系数矩阵，后面是未知数和向量。这里已经有 \(2\) 个未知数，而以后我们可能会碰到更多的未知数。

未知数向量我们一般用加粗的 X 来表示。

最右侧也是向量，用 \(b\) 表示。

所以，线性方程组可以写成 \(A\)X\(=b\)

下面，做本例的行图像：

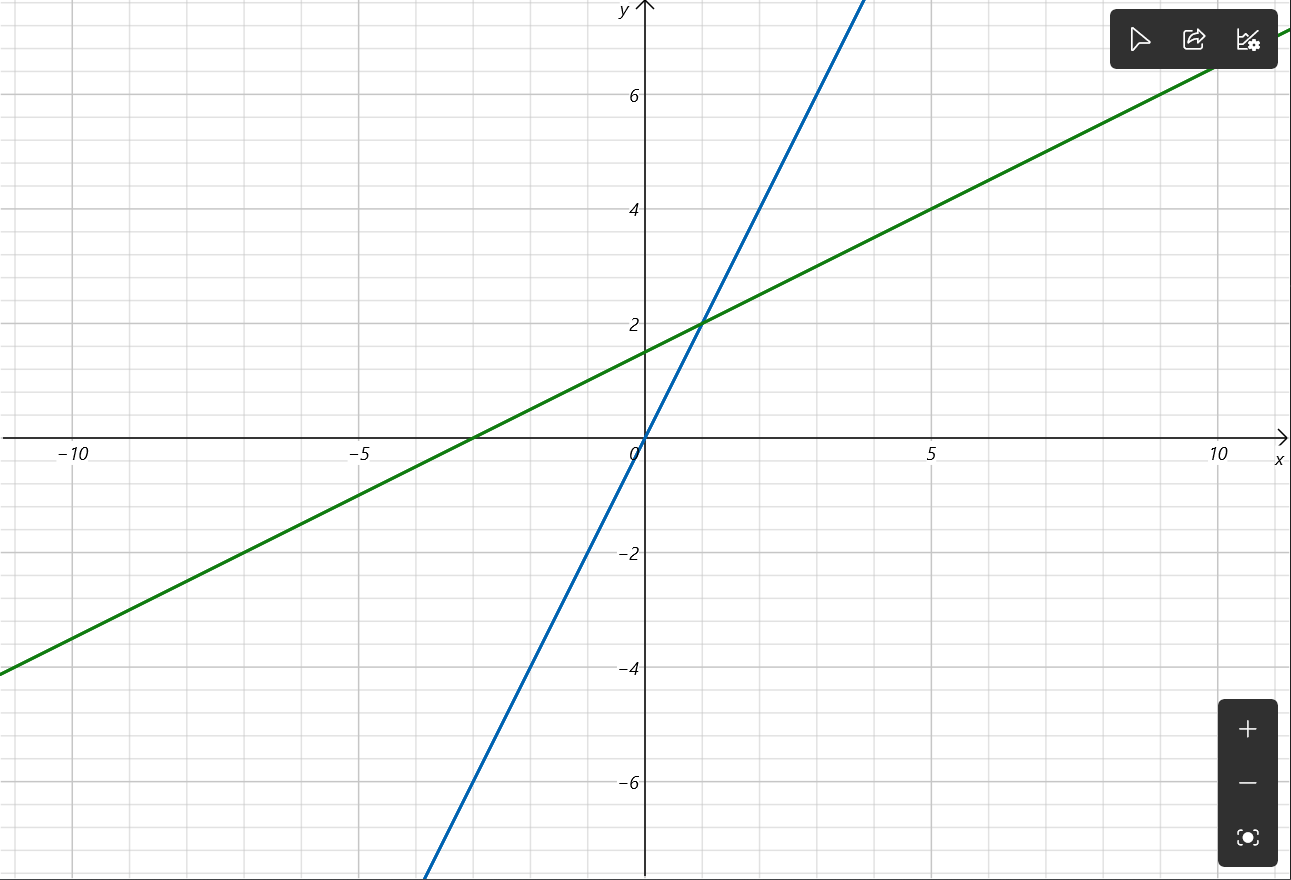
两个函数表达式分别是 \(2x-y=0\) 和 \(-x+2y=3\) 。

观察行图像，两条直线的交点就是我们关注的焦点，很显然该点应该是 \((1，2)\)。

显然，该方程的解为: \( \begin{cases} x=1\\ y=2 \end{cases} \) 检验成立。

下面我们进入列图像。注意，列图像才是关键。

\[x\begin{bmatrix} 2\\-1 \end{bmatrix} +y\begin{bmatrix} -1\\2 \end{bmatrix} =\begin{bmatrix} 0\\3 \end{bmatrix} \]

这个方程的目的是寻找如何将向量\(\begin{bmatrix} 2\\-1 \end{bmatrix}\) 和 \(\begin{bmatrix} -1\\2 \end{bmatrix}\) 正确组合从而得到 \(\begin{bmatrix} 0\\3 \end{bmatrix}\) , 这就需要正确的线性组合。

“线性组合(\(Linear\,Combination\,of\,columns)\)” 是贯穿整个文章集合的基本方法。

显然，这些向量有两个分量可以这样作图：

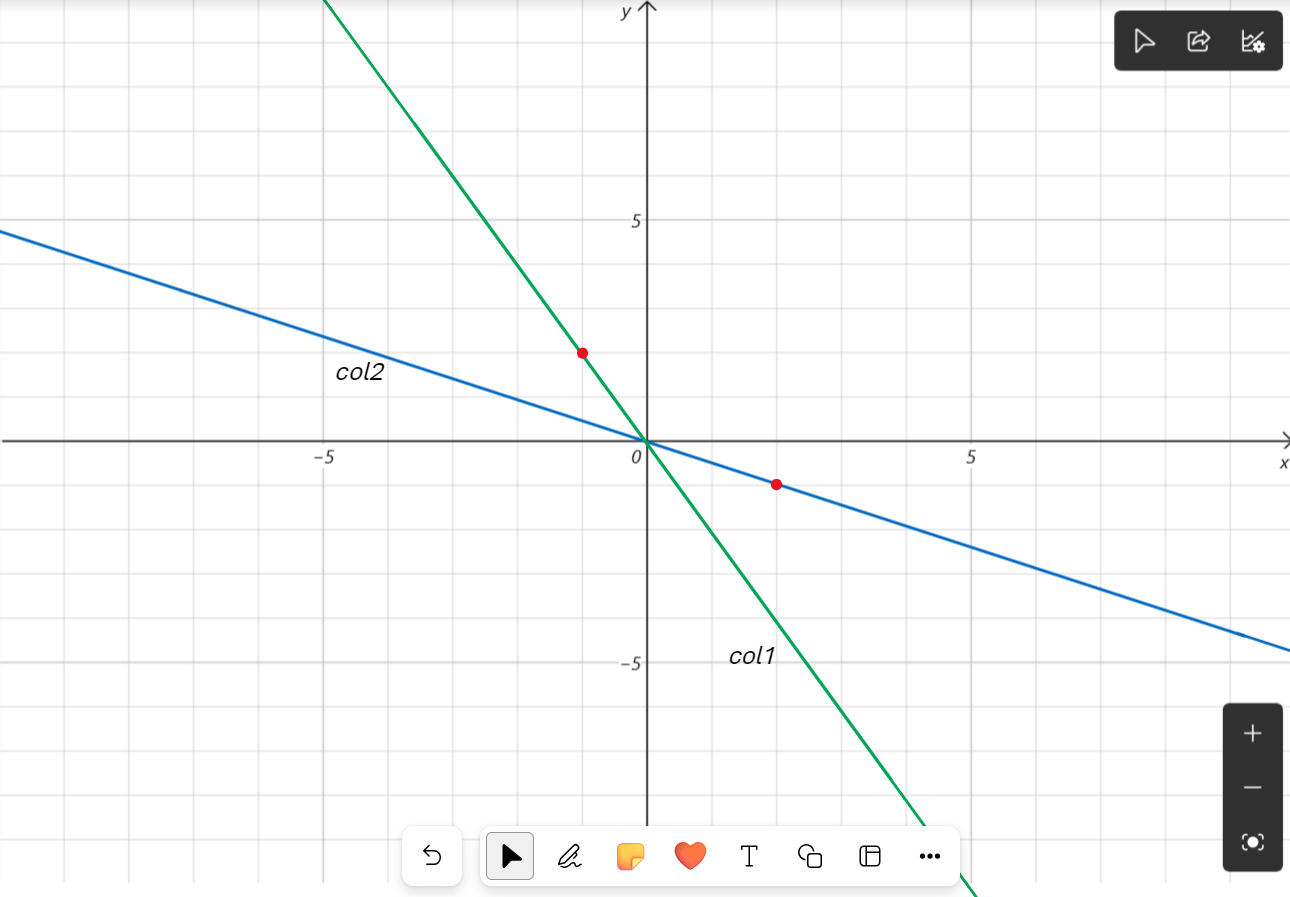
根据图像我们得出正确的组合应该是 \(1\) 个列 \(1\) 和 \(2\) 个列 \(2\)。

即有：

\[1\begin{bmatrix} 2\\-1 \end{bmatrix} +2\begin{bmatrix} -1\\2 \end{bmatrix} =\begin{bmatrix} 0\\3 \end{bmatrix} \]

然后，我们操作 \(+\begin{bmatrix} 2\\-1 \end{bmatrix}\) ,直观一点就是向左移动一位然后向上移动一位。

如图：

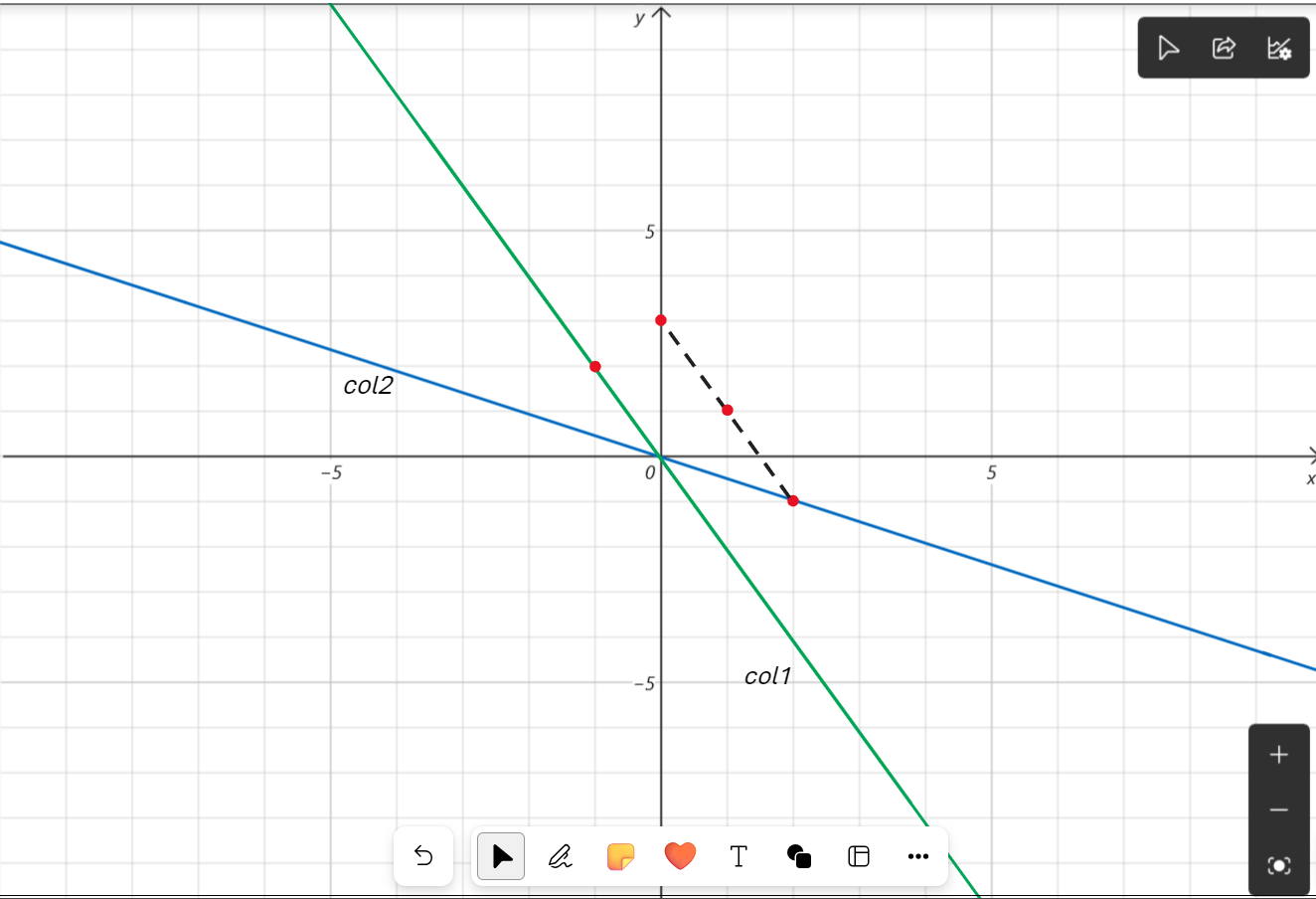
然而很显然，图中的蓝点就是我们所求的 \(b\)

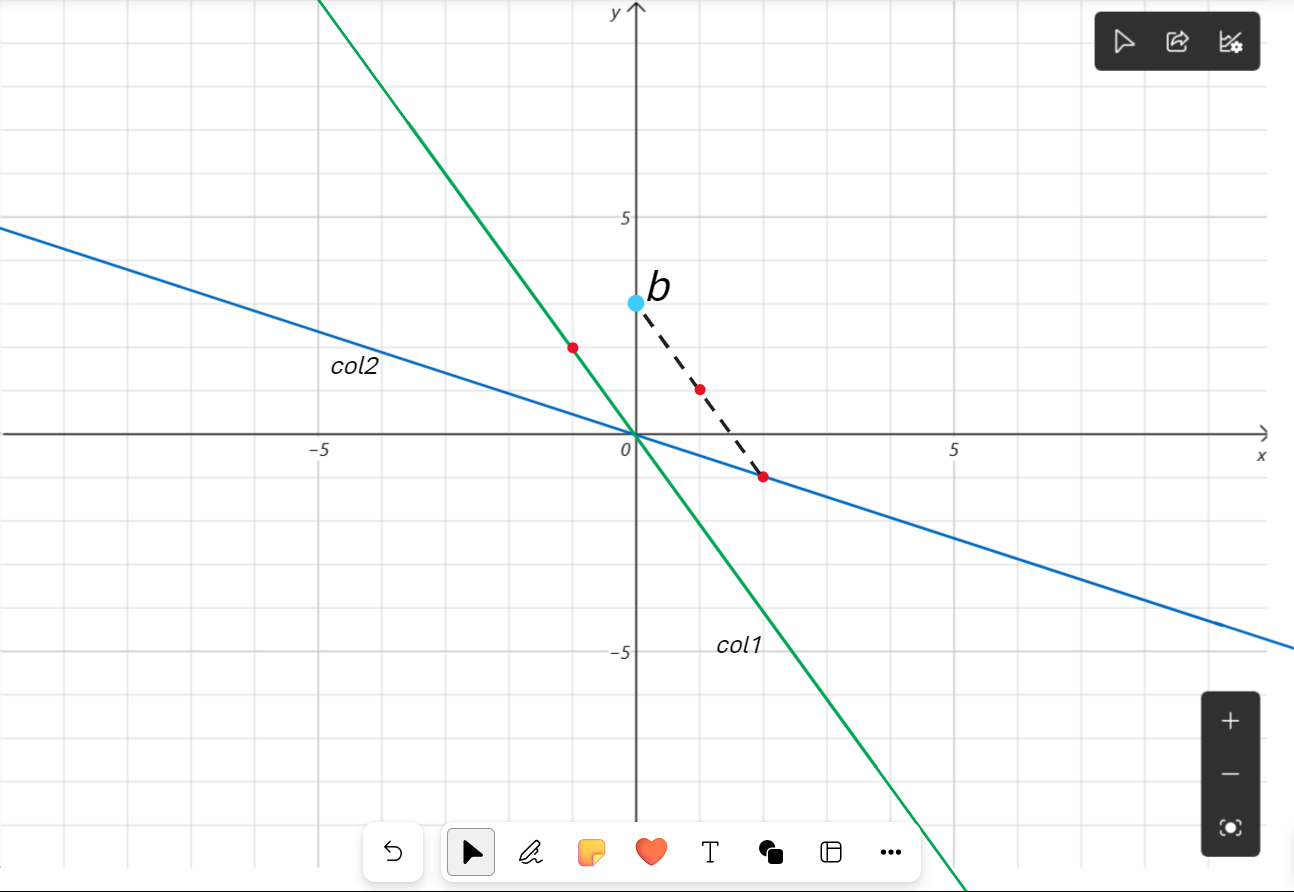
它是怎么得来的？对于第一个分量，\(2\) 和 \((-2)\) 组合得到 \(0\) , 对于第二个分量 ,\(-1\) 和 \(4\) 组合得到 \(3\)。看这个图象，我用两列进行组合，从而得到 \(b\) 即 \((0,3)\)。

因此，线性组合非常关键。

现在，我们思考一个问题，所有的线性组合是什么？

我们回到 \(x\) 和 \(y\) ：\( x\begin{bmatrix} 2\\-1 \end{bmatrix} +y\begin{bmatrix} -1\\2 \end{bmatrix} =\begin{bmatrix} 0\\3 \end{bmatrix} \) 。

问题就变成，我们选取所有的 \(x\) 和 \(y\) , 所有的组合，结果会如何？结果是我们会得到任意的右侧向量，这两个向量组合会布满整个坐标平面。这个问题以后还会遇到，到时候再深入研究。

线性组合可以求出 \(b\) , 而所有的线性组合可以求出所有可能的右侧向量,这是本章的基本思想。

接下来，我们来看三元一次方程的情况：

\[\begin{cases} 2x \, -y \, \, \, \, \, \, \, \, \, \, \, \, \, =0\\ -x+2y-z =-1\\ \, \, \, \, \, \, \, \, \, \, -3y+4z=4 \end{cases} \]

我们可以知道

\[A=\begin{bmatrix} 2&-1&0\\ -1&2&-1\\ 0&3&4 \end{bmatrix} ,b=\begin{bmatrix} 0\\-1\\4 \end{bmatrix} \]

如何解决它呢？行图像是一种方法，列图像又是另外一种方法。记住矩阵形式，它可以使问题简化。

我们先来看行图像：

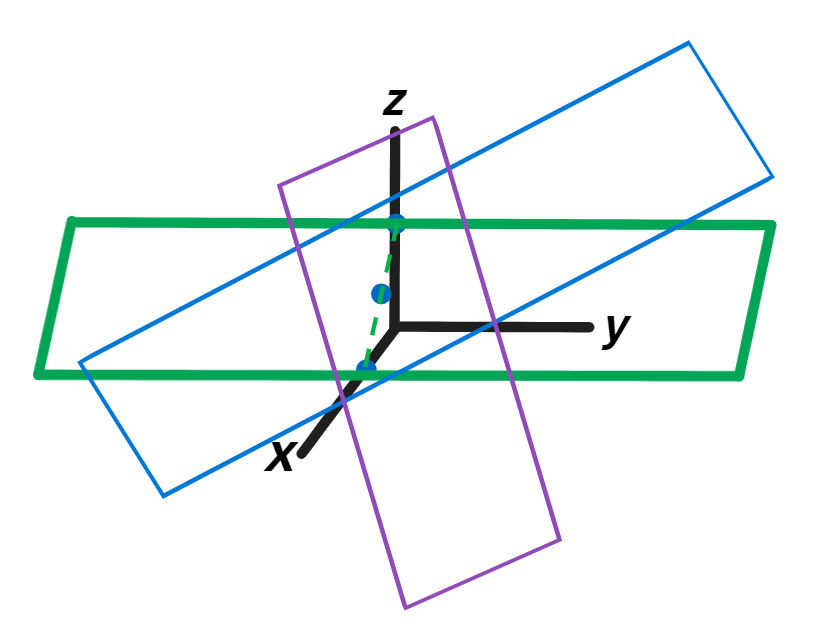
我们可以看到这是一个三维的坐标系，两个平面交于一线，三个平面交于一点而这个点就是答案。你会发现多维的行图像画起来非常复杂，看上去十分抽象，如果这是四维的话就更难表达，所以我一般更倾向于列图像。

移步到列图像：

\[x\begin{bmatrix} 2\\-1\\0 \end{bmatrix} +y\begin{bmatrix} -1\\2\\-3 \end{bmatrix} +z\begin{bmatrix} 0\\-1\\4 \end{bmatrix} =\begin{bmatrix} 0\\-1\\4 \end{bmatrix} \]

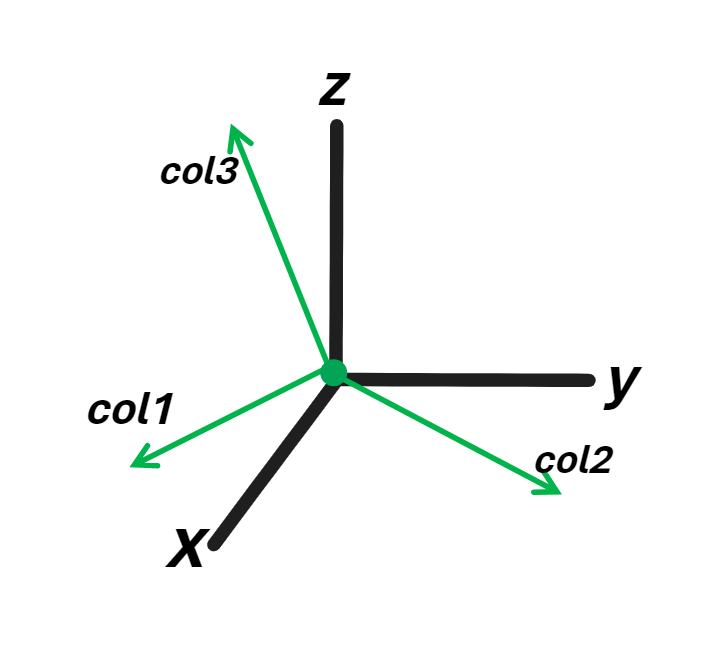
这道题，我们发现左侧的第三个向量和右侧的向量是相同的，所以我们只需要留下\(z\begin{bmatrix} 0\\-1\\4 \end{bmatrix} \)即可。

很显然, \(x=0,y=1,z=1\) 即为答案，而图中向量 \(col_3\) 的顶点即为所求 \(b\)。

我们在下一章会讲解如何求所有情况下的\(x\),\(y\),\(z\),下面回来讨论大图。

"大图"是指保证左侧矩阵不变，考虑不同右侧向量。

我换了一个右侧向量：\( x\begin{bmatrix} 2\\-1\\0 \end{bmatrix} +y\begin{bmatrix} -1\\2\\-3 \end{bmatrix} +z\begin{bmatrix} 0\\-1\\4 \end{bmatrix} =\begin{bmatrix} 1\\1\\-3 \end{bmatrix} \)

虽然换了一个右侧向量，它仍然十分特殊，我把它换成了前两列之和。

很显然，对于新的有右侧向量，答案是 \(x=1,y=1,z=0\)。

这样一来，行图像中就有 \(3\) 个不同的平面，交于点 \((1,1,0)\) ，而列图像三列没有变化只需要重新组合。

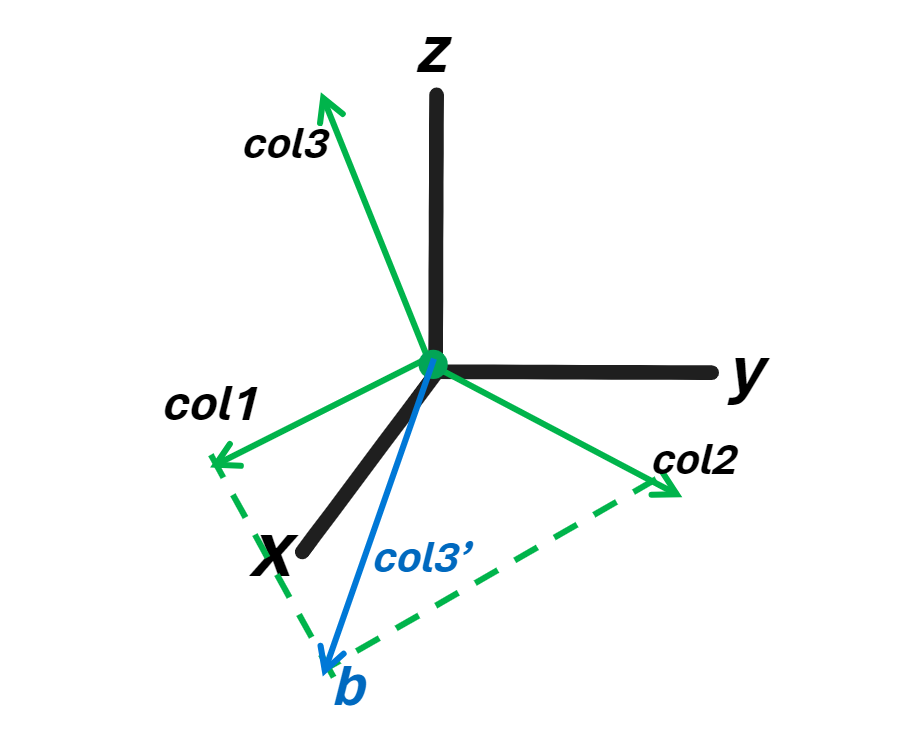
现在思考所有的 \(b\) 的值，对于任意的值 \(b\) 都有解吗？

也就是代数问题：对于任意 \(b\) , 是否都能求解 \(A\)X\(=b\) ?

而用线性组合的语言来说就是：对于任意向量 \(b\) ，列的线性组合是否能覆盖整个三维空间？

\(A\)x 指的是矩阵 \(\times\) 向量。

显然，对于这个矩阵 \(A\) 答案是肯定的。这个矩阵是一个非奇异且可逆的矩阵。然而，对于其他的一些矩阵，答案很可能是否定的。

什么时候会这样？举个例子吧，如果三个列向量同属于一个平面，那组合也出现在这个平面上，问题就出现了。

假如 \(col_3 = col_1 + col_2\) 答案就会是否定的。因为如果列 \(3\) 等于列 \(2\) 和列 \(1\) 的和，无论怎么组合，都得不出平面以外的向量。所能得到的右侧向量 \(b\) 必然属于这个平面内。因此，当 \(b\) 处在平面内，方程组有解，但大部分不在平面内的 \(b\) 均是无法构造的。

这种情况称作奇异，矩阵并非可逆。不是任何 \(b\) 都有解 。

我们原来问题的答案显然是否定的。

接下来，我们来思考一个有趣的问题：

假设有 \(9\) 个方程 \(9\) 个未知数，这样我们就会有 \(9\) 列,每一列都是 \(9\) 维空间的向量，然后额可以考虑它的线性组合，这样就得到了九维空间中九个向量的线性组合，我们通过线性组合得到正确的右侧向量 \(b\)，同样的问题：是否对于任意的右侧向量都有解？

当然，这还是取决于九个列向量。有时答案是肯定的，比如随机矩阵，答案就是肯定的 \(MatLab\) 中使用随机命令，随机取一个 \(9 \times 9\) 的矩阵,这个矩阵将具有非奇异、可逆，一切美好的性质。但如果我选择一些互不独立的列向量，比如 \(9\) 列向量相当于 \(8\) 列向量有一列向量毫无贡献,这样就会有一些 \(b\) 无法求得。

想象一下 \(9\) 维空间中 \(9\) 个向量的组合，这是线性代数中必须掌握的中心内容。九个列向量及其组合将能够覆盖整个九维空间，但如果第九列碰巧等于第八列，这时的线性组合就只能覆盖某种平面，只能覆盖九维空间中的某八维平面，最后的求解只能在这个八维平面上展开。

但现在，我们还是集中关注非奇异矩阵的情况，这种情况下只要正确组合就可以得到任何的 \(b\) ,接下来要讲到的是方程组的矩阵形式。

现在我先构造一个矩阵:\(\begin{bmatrix} 2&5\\1&3 \end{bmatrix} \begin{bmatrix} 1\\2 \end{bmatrix} \)

它们如何相乘？我令 \(A_{i,j}\) 表示 \(A\) 矩阵的第 \(i\) 行第 \(j\) 列，理解意思就行，这里可能不是特别严谨。

它们相乘简单表示就是：

\[c_{i,j} = \sum ^ {n}_{k=1} a_{i,k} \times b_{k,j} \]

这一点很好理解，不过多赘述。不过还是提醒一点，大家计算时可以将 \(A\)X 看作是 \(A\) 各列的线性组合，这样的话在向量数量较多的情况下会更加方便一点。

本章到此结束。

预告：在下一章节，我会说到使用 "消元法" 来解决问题。