(十五)从零开始学人工智能-深度学习基础2
一、循环神经网络基础
在前面的文章中,介绍了全连接神经网络(DNN)和卷积神经网络(CNN),以及它们的训练和使用。回忆一下,它们都是能单独的处理一个个的输入,前一个输入和后一个输入是完全没有关系的。然后,现实当中是,某些任务需要能够更好的处理序列性质的信息,即前面的输入和后面的输入是有关系的。例如,当我们理解一句话意思时,孤立的理解这句话的每个词都是不够的,我们需要处理这些词连接起来的整个序列;当我们处理视频时,也不能只单独的去分析每一帧,而要分析这些帧连接起来的整个序列。这时,使用我们前文介绍的DNN和CNN是不够的,而需要用到深度学习领域中另一类非常重要的神经网络:循环神经网络(Recurrent Neural Network, RNN)。RNN种类繁多,过程繁琐,本部分首先对其结构进行剥茧抽丝,以理解RNNs及其训练算法;进一步地,介绍两中常见的RNN类型:长短时记忆网络(Long Short-Term Memory Network,LSTM),门控循环单元(Gated Recurrent Unit, GRU)。
1.1 从语言模型开始
为什么要从语言模型开始呢?因为,RNN是在自然语言处理领域中最先被用起来的,例如,RNN可以构建语言模型。那什么是语言模型呢?
我们可以让电脑做这样一个练习:写出一个句子前面的一些词,然后,让电脑帮我们写出接下来的一个词。比如下面这句话:
我昨天上学迟到了,老师批评了____。
在这个句子中,接下来的词最有可能的是“我”,而不是“小明”,更不会是“吃饭”。
在这个例子中,语言模型是这样的一个东西:给定一个一句话前面的部分,预测接下来最有可能的一个词是什么。
语言模型是对一种语言的特征进行建模,它有很多用处。比如在语音转文本(STT)的应用中,声学模型输出的结果,往往是若干个可能的候选词,这时候就需要语言模型来从这些候选词中选择一个最有可能的。当然,它同样也可以用在图像到文本的识别中国(OCR)。
在使用RNN之前,语言模型主要采用N-Gram算法。N是一个自然数,比如2或者3.它的含义是:假设一个词出现的概率只与前面N个词相关。我们以2-Gram为例,对这句话给出部分进行分词:
我|昨天|上学|迟到|了|,|老师|批评|了|____。
如果用2-Gram进行建模,那么电脑在预测的时候,只会看到前面的“了”,然后,电脑会在语料库中,搜索“了”后面最有可能的一个词。不管最后电脑选择的是不是“我”,显然这个模型是不靠谱的,因为“了”前面说了那么一大推实际上是没有用到的。如果使用3-Gram模型呢,会搜索“批评了”后面最有可能的词,感觉比2-Gram靠谱了不少,但还是远远不够的。因为这句话最关键的信息“我”,远在9个词之前。
看到这儿,大家可能会想,可以继续提升N的值呀,比如4-Gram、5-Gram、\(\dots\)。实际上,大家再深入想一下就会发现,这个想法是没有实用性的,因为当我们想处理任意长度的句子时,N设为多少都是不合适的;另外,模型的大小和N的关系是指数级的,4-Gram模型就会占用海量的存储空间。
所以,就该轮到RNN出场了,RNN理论上可以往前看(或往后看)任意多个词。
1.2 什么是循环神经网络?
循环神经网络种类繁多,我们先从最简单的基础循环神经网络开始吧~
1.2.1 基本循环神经网络
下图是一个简单的循环神经网络,它由输入层、一个隐藏层和一个输出层组成:
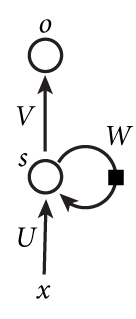
循环神经网络的实在是太难画出来了,网上所有大神们都不得不用了这种抽象的手法。不过,仔细看的话,如果把上面有\(W\)的那个带箭头的圈去掉,它就变成了最普通的全连接网络了。\(x\)是一个向量,它表示输入层的值(这里没有画出来表示输入层神经元节点的圆圈),\(s\)是一个向量,它表示隐藏层的值(这里隐藏层画了一个节点,你也可以想象这一层其实是多个节点,节点数目与向量\(s\)的维度相同);\(U\)是输入层到隐藏层的权重矩阵;\(O\)也是一个向量,它表示输出层的值;\(V\)是隐藏层到输出层的权重矩阵。那么,现在我们来看看\(W\)是什么,循环神经网络的隐藏层的值\(s\)不仅仅取决于当前这次输入\(x\),还取决于上一次隐藏层的值\(s\)。权重矩阵\(W\)就是隐藏层上一次的值作为这一次的输入的权重。
如果我们把上面的图展开,循环神经网络的也可以画成下面的样子:

现在看上去就比较清晰了,这个网络在\(t\)时刻接收到输入\(x_t\)之后,隐藏层的值是\(s_t\),输出值是\(o_t\)。关键一点是,\(s_t\)的值不仅仅取决于\(x_t\),还取决于\(s_{t-1}\)。我们可以用下面的公式来表示循环神经网络的计算方法:
$$o_t=g(Vs_t) \tag{1}$$
$$s_t = f(Ux_t+Ws_{t-1}) \tag{2}$$
式1是输出层的计算公式,输出层是全连接层,也就是它的节点都是和隐藏层的每个节点相连。\(V\)是一个输出层的权重矩阵,\(g\)是激活函数。式2是隐藏层的计算公式,它是循环层。\(U\)是输入\(x\)的权重矩阵,\(W\)是上一次输出值\(s_{t-1}\)作为这一次输入的权重矩阵,\(f\)是激活函数。
从上面的公式我们可以看出,循环层和全连接层的区别就是循环层多了一个权重矩阵\(W\)。
如果反复把式2带入到式1,我们可以得到:
$$\begin{aligned}o_t &=g(Vs_t) \ &=Vf(Ux_1+Ws_{t-1})\ &=Vf(Ux_t+Wf(Ux_{t-1}+Ws_{t-2}))\&=Vf(Ux_t+Wf(Ux_{t-1}+Wf(Ux_{t-2}+Ws_{t-3})))\ &=Vf(Ux_t+Wf(Ux_{t-1}+Wf(Ux_{t-2}+Wf(Ux_{t-3}+\dots)))) \end{aligned}$$
从上面可以看出,循环神经网络的输出值\(o_t\),是受前面历次输入值\(X_t\)、\(X_{t-1}\)、\(X_{t-2}\)、\(\dots\)影响的,这也是为什么循环神经网络可以往前看任意多个输入值的原因。
1.2.2 双向循环神经网络
对于语言模型来说,很多时候光看前面的词是不够的,比如下面这句话:
我的手机坏了,我打算____一部新手机。
可以想象的是,如果我们只看到横线前面的词,手机坏了,那么我是打算修一修?换一部新的手机?还是哭哭?这些都是无法确定的。但是如果我们还看到横线后面的词是“一部新手机”,那么,横线上的词填“买”的概率就大得多了。
在上一节中的基本循环神经网络是无法对此进行建模的,因此,我们需要双向循环神经网络,如下图所示:

当遇到这种从未来穿越回来的场景时,难免处于懵逼的状态。不过我们还是可以用屡试不爽的老办法:先分析一个特殊场景,然后再总结一般的规律。我们先考虑上图中,\(y_2\)的计算。
从上图可以看出,双向循环神经网络的隐藏层要保存两个值,一个\(A\)参与正向计算,另一个值\(A'\)参与计算。最终的输出值\(y_2\)取决于\(A_2\)和\(A_2'\)。其计算方法为:
\(y_2=g(VA_2+V'A_2')\)
其中\(A_2\)和\(A_2'\)的计算为:
\(A_2=f(WA_1+UX_2)\)
\(A_2'=f(W'A_3'+U'X_2)\)
至此,我们已经可以看出一般的规律:正向计算时,隐藏层的值\(S_t\)与\(S_{t-1}\)有关;反向计算时,隐藏层的值\(S_t'\)与\(S_{t+1}'\)有关;最终的输出取决于正向和反向计算的加和。现在,我们仿照式1和式2,写出双向循环神经网络的计算方法:
\(O_t=g(VS_t+V'S_t')\)
\(S_t=f(UX_t+WS_{t-1})\)
\(S_t'=f(U'X_t+W'S_{t+1}')\)
从上面的三个公式可以看到,正向计算和反向计算不共享权重,也就是说\(U\)和\(U'\),\(W\)和\(W'\),\(V\)和\(V'\)都是不同的权重矩阵。
1.2.3 深度循环神经网络
前面我们介绍的循环神经网络只有一个隐藏层,当然了,也可以堆叠两个以上的隐藏层,这样就得到了深度循环神经网络。如下图所示:

我们把第\(i\)个隐藏层的值表示为\(S_t^{(i)}\)、\(S_t'^{(i)}\),则深度循环神经网络的计算方式可以表示为:
\(O_t=g(V^{(i)}S_t^{(i)}+V'^{(i)}S_t'^{(i)})\)
\(S_t^{(i)}=f(U^{(i)}S_t^{i-1}+W^{(i)}S_{t-1})\)
\(S_t'^{(i)}=f(U'^{(i)}S_t'^{(i-1)}+W'^{(i)}S_{t+1}')\)
\(\cdots\)
\(S_t^{(1)}=f(U^{(1)}X_t+W^{(1)}S_{t-1})\)
\(S_t'^{(1)}=f(U'^{(1)}X_t+W'^{(1)}S_{t+1}')\)
1.3 循环神经网络的训练
1.3.1 循环神经网络的训练算法:BPTT
\(BPTT\)算法是针对循环层的训练算法,它的基本原理和\(BP\)算法是一样的,也包含同样的三个步骤:
前向计算每个神经元的输出值;
反向计算每个神经元的误差项\(\delta_j\)值,它是误差函数\(E\)对神经元\(j\)的加权输入\(net_j\)的偏导数;
计算每个权重的梯度。
循环层如下图所示:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-a8kYlBqb-1583227061275)(./img2/5.png)]
最后再用随机梯度下降算法更新权重。
前向计算
使用前面的式2对循环层进行前向计算:
\(S_t=f(UX_t+WS_{t-1})\)
注意:上面的\(S_t\)、\(X_t\)、\(S_{t-1}\)都是向量,用黑体字母表示(在这里都用大写替代表示了😂,将就看吧❤️);而\(U\)、\(V\)是矩阵,用大写字母表示。向量的下标表示时刻,例如,\(S_t\)表示在\(t\)时刻向量\(S\)的值。
我们假设输入向量\(X\)的维度是\(m\),输出向量\(S\)的维度是\(n\),则矩阵\(U\)的维度是\(n\) x \(m\),矩阵\(W\)的维度是\(n\) x \(n\)。下面是我们上式展开成矩阵的样子,看起来更直观一些:
$$\left[ \begin{matrix} s_1^t \ s_2^t \ \vdots \ s_n^t \end{matrix} \right]=f(\left[ \begin{matrix} u_{11} & u_{12} & \cdots & u_{1m}\ u_{21} & u_{22} & \cdots & u_{2m} \ \vdots & \vdots & \ddots & \vdots \ u_{n1} & u_{n2} & \cdots & u_{nm} \end{matrix} \right]\left[ \begin{matrix} x_1 \ x_2 \ \vdots \ x_m \end{matrix} \right]+\left[ \begin{matrix} w_{11} & w_{12} & \cdots & w_{1n}\ w_{21} & w_{22} & \cdots & w_{2n} \ \vdots & \vdots & \ddots & \vdots \ w_{n1} & w_{n2} & \cdots & w_{nm} \end{matrix} \right]\left[ \begin{matrix} s_1^{t-1} \ s_2^{t-1} \ \vdots \ s_n^{t-1} \end{matrix} \right]) $$
上式中,手写体字母表示向量的一个元素,它的下标表示它是这个向量的第几个元素,它的上标表示第几个时刻。例如,\(s_j^t\)表示向量\(S\)的第\(j\)个元素在\(t\)时刻的值;\(u_{ji}\)表示输入层第\(i\)个神经元到循环层第\(j\)个神经元的权重;\(w_{ji}\)表示循环层第\(t-1\)时刻的第\(i\)个神经元到循环层第\(t\)个时刻的第\(j\)个神经元的权重。
误差项的计算
\(BTPP\)算法将第\(l\)层\(t\)时刻的误差项\(\delta_t^l\)值沿两个方向传播,一个方向是其传递到上一层网络,得到\(\delta_t^{l-1}\),这一部分只和权重矩阵\(U\)相关;另一个方向是将其沿时间线传递到初始时刻\(t_1\),得到\(\delta_1^l\),这部分只和权重矩阵\(W\)相关。
我们用向量\(net_t\)表示神经元在\(t\)时刻的加权输入,得到:
\(net_t=UX_t+WS_{t-1}\)
\(S_{t-1}=f(net_{t-1})\)
因此:
\(\frac{\partial net_t}{\partial net_{t-1}}=\frac{\partial net_t}{\partial S_{t-1}}\frac{\partial S_{t-1}}{\partial net_{t-1}}\)
约定:我们使用\(a\)表示列向量,用\(a^T\)表示行向量。
上式第一项是向量函数对向量求导,其结果为\(Jacobian\)矩阵:
$$\begin{aligned}\frac{\partial net_t}{\partial S_{t-1}} &=\left[ \begin{matrix} \frac{\partial net_1^t}{\partial S_1^{t-1}} & \frac{\partial net_1^t}{\partial S_2^{t-1}} & \cdots & \frac{\partial net_1^t}{\partial S_n^{t-1}} \ \frac{\partial net_2^t}{\partial S_1^{t-1}} & \frac{\partial net_2^t}{\partial S_2^{t-1}} & \cdots & \frac{\partial net_2^t}{\partial S_n^{t-1}} \ \vdots & \vdots & \ddots & \vdots \ \frac{\partial net_n^t}{\partial S_1^{t-1}} & \frac{\partial net_n^t}{\partial S_2^{t-1}} & \cdots & \frac{\partial net_n^t}{\partial S_n^{t-1}} \end{matrix} \right] \ &=\left[ \begin{matrix} w_{11} & w_{12} & \cdots & w_{1n}\ w_{21} & w_{22} & \cdots & w_{2n} \ \vdots & \vdots & \ddots & \vdots \ w_{n1} & w_{n2} & \cdots & w_{nm} \end{matrix} \right]\ &=W \end{aligned}$$
同理,上式第二项也是一个\(Jacobian\)矩阵:
$$\begin{aligned}\frac{\partial S_{t-1}}{\partial net_{t-1}} &=\left[ \begin{matrix} \frac{\partial S_1^{t-1}}{\partial net_1^{t-1}} & \frac{\partial S_1^{t-1}}{\partial net_2^{t-1}} & \cdots & \frac{\partial S_1^{t-1}}{\partial net_n^{t-1}} \ \frac{\partial S_2^{t-1}}{\partial net_1^{t-1}} & \frac{\partial S_2^{t-1}}{\partial net_2^{t-1}} & \cdots & \frac{\partial S_2^{t-1}}{\partial net_n^{t-1}} \ \vdots & \vdots & \ddots & \vdots \ \frac{\partial S_n^{t-1}}{\partial net_1^{t-1}} & \frac{\partial S_n^{t-1}}{\partial net_2^{t-1}} & \cdots & \frac{\partial S_n^{t-1}}{\partial net_n^{t-1}} \end{matrix} \right] \ &=\left[ \begin{matrix} f'(net_1^{t-1}) & 0 & \cdots & 0 \ 0 & f'(net_2^{t-1}) & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & f'(net_n^{t-1}) \end{matrix} \right]\ &=diag[f'(net_{t-1})] \end{aligned}$$
\(diag[a]\)表示根据向量\(a\)创建一个对角矩阵,即
$$\begin{aligned}diag(a) &=\left[ \begin{matrix} a_1 & 0 & \cdots & 0 \ 0 & a_2 & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & a_n \end{matrix} \right] \end{aligned}$$
最后,将两项合在一起,得到:
$$\begin{aligned}\frac{\partial net_t}{\partial net_{t-1}} &=\frac{\partial net_t}{\partial S_{t-1}}\frac{\partial S_{t-1}}{\partial net_{t-1}} \ &=Wdiag[f'(net_{t-1})] \
&=\left[ \begin{matrix} w_{11}f'(net_1^{t-1}) & w_{12}f'(net_2^{t-1}) & \cdots & w_{1n}f'(net_n^{t-1})\ w_{21}f'(net_1^{t-1}) & w_{22}f'(net_2^{t-1}) & \cdots & w_{2n}f'(net_n^{t-1}) \ \vdots & \vdots & \ddots & \vdots \ w_{n1}f'(net_1^{t-1}) & w_{n2}f'(net_2^{t-1}) & \cdots & w_{nm}f'(net_n^{t-1}) \end{matrix} \right] \end{aligned}$$
上式描述了将\(\delta\)沿着时间往前传递一个时刻的规律,有了这个规律,我们就可以求得任意时刻\(k\)的误差项\(\delta_k\):
$$\begin{aligned}\delta_k^T &=\frac{\partial E}{\partial net_k} \
&=\frac{\partial E}{\partial net_t}\frac{\partial net_t}{\partial net_k} \
&=\frac{\partial E}{\partial net_t}\frac{\partial net_t}{\partial net_{t-1}}\frac{\partial net_{t-1}}{\partial net_{t-2}} \cdots \frac{\partial net_{k+1}}{\partial net_k} \
&=Wdiag[f'(net_{t-1})]Wdiag[f'(net_{t-2})] \cdots Wdiag[f'(net_k)]\delta_t^l \
&=\delta_tT\prod_{i=k}Wdiag[f'(net_i)]
\end{aligned} \tag{3} $$
上式就是将误差沿时间反向传播的算法。
误差项传递到上一层
循环层将误差项反向传播到上一层网络,与普通的全连接是完全一样的,这在全面的文章中已经详细介绍过,此处仅简要介绍:
循环层的加权输入\(net^l\)与上一层的加权输入\(net^{l-1}\)关系如下:
\(net_t^l=Ua_t^{l-1}+WS_{t-1}\)
\(a_t^{l-1}=f^{l-1}(net_t^{l-1})\)
上式中的\(net_t^l\)是第\(l\)层神经元的加权输入(假设第\(l\) 层是循环层);\(net_t^{l-1}\)是第\(l-1\)层神经元的加权输入;\(a_t^{l-1}\)是第\(l-1\)层神经元的输出;\(f^{l-1}\)是第\(l-1\)层的激活函数。
$$\begin{aligned}\frac{\partial net_t^l}{\partial net_t^{l-1}} &=\frac{\partial net^l}{\partial a_t^{l-1}}\frac{\partial a_t^{l-1}}{\partial net_t^{l-1}} \
&=Udiag[f'{l-1}(net_t)]
\end{aligned}$$进一步地,
$$\begin{aligned}(\delta_t{l-1})T &=\frac{\partial E}{\partial net_t^{l-1}} \
&=\frac{\partial E}{\partial net_t^l}\frac{\partial net_t^l}{\partial net_t^{l-1}} \
&=(\delta_tl)TUdiag[f'{l-1}(net_t)]
\end{aligned}$$该式即为将误差传递到上一层的算法。
权重梯度的计算
现在,终于来到了\(BPTT\)算法的最后一步:计算每个权重的梯度。
首先,我们计算误差函数\(E\)对权重矩阵\(W\)的梯度\(\frac{\partial E}{\partial W}\)。

上图展示了我们到目前为止,在前面两步计算得到的量,包括每个时刻\(t\)的循环输出值\(S_t\),以及误差项\(\delta_t\)。
回忆一下全连接网络的权重梯度计算算法:只要知道了任意一个时刻的误差项\(\delta_t\),以及上一个时刻循环层的输出值\(S_{t-1}\),就可以按照下面的公式求出权重矩阵在\(t\)时刻的梯度\(\nabla_{W_t}E\):
$$\begin{aligned}\nabla_{W_t}E &=\left[ \begin{matrix} \delta_1ts_1 & \delta_1ts_2 & \cdots & \delta_1ts_n \ \delta_2ts_1 & \delta_2ts_2 & \cdots & \delta_2ts_n \ \vdots & \vdots & \ddots & \vdots \ \delta_nts_1 & \delta_nts_2 & \cdots & \delta_nts_n \end{matrix} \right] \end{aligned} \tag{4}$$
式中,\(\delta_i^t\)表示\(t\)时刻误差项向量的第\(i\)个分量;\(s_i^{t-1}\)表示\(t-1\)时刻循环层第\(i\)个神经元的输出值。
式4推导
由前文知\(net_t=UX_t+WS_{t-1}\),即
$$\begin{aligned}\left[ \begin{matrix} net_1^t \ net_2^t \ \vdots \ net_n^t \end{matrix} \right]
&=UX_t+\left[ \begin{matrix} w_{11} & w_{12} & \cdots & w_{1n}\ w_{21} & w_{22} & \cdots & w_{2n} \ \vdots & \vdots & \ddots & \vdots \ w_{n1} & w_{n2} & \cdots & w_{nm} \end{matrix} \right]\left[ \begin{matrix} s_1^{t-1} \ s_2^{t-1} \ \vdots \ s_n^{t-1} \end{matrix} \right] \
&=UX_t+\left[ \begin{matrix} w_{11}s_1^{t-1} & w_{12}s_2^{t-1} & \cdots & w_{1n}s_n^{t-1}\ w_{21}s_1^{t-1} & w_{22}s_2^{t-1} & \cdots & w_{2n}s_n^{t-1} \ \vdots & \vdots & \ddots & \vdots \ w_{n1}s_1^{t-1} & w_{n2}s_2^{t-1} & \cdots & w_{nm}s_n^{t-1} \end{matrix} \right]
\end{aligned}$$因为对\(W\)求导与\(UX_t\)无关,我们不再考虑。现在,我们考虑对权重\(w_{ji}\)求导。通过观察上式我们可以看到\(w_{ji}\)只与\(net_j^t\)有关,所以:
$$\begin{aligned}\frac{\partial E}{\partial w_{ji}} &=\frac{\partial E}{\partial net_j^t}\frac{\partial net_j^t}{\partial w_{ji}} \
&=\delta_jts_i
\end{aligned}$$按照上面的规律就可以生成式4里面的矩阵。
我们已经求得了权重矩阵\(W\)在\(t\) 的梯度\(\nabla_{W_t}E\),最终的梯度\(\nabla_WE\)是各个时刻的梯度之和:
$$\begin{aligned}\nabla_WE &= \Sigma_{i=1}^t\nabla_{W_t}E \
&=\left[ \begin{matrix} \delta_11s_10 & \delta_11s_20 & \cdots & \delta_11s_n0 \ \delta_21s_10 & \delta_21s_20 & \cdots & \delta_21s_n0 \ \vdots & \vdots & \ddots & \vdots \ \delta_n1s_10 & \delta_n1s_20 & \cdots & \delta_n1s_n0 \end{matrix} \right]+\cdots+\left[ \begin{matrix} \delta_1ts_1 & \delta_1ts_2 & \cdots & \delta_1ts_n \ \delta_2ts_1 & \delta_2ts_2 & \cdots & \delta_2ts_n \ \vdots & \vdots & \ddots & \vdots \ \delta_nts_1 & \delta_nts_2 & \cdots & \delta_nts_n \end{matrix} \right]
\end{aligned}\tag5{} $$
式5就是计算循环层权重矩阵\(W\)梯度的公式。
前面已经介绍了\(\nabla_WE\)的计算方法,看上去还是比较直观的。然而,读者也许会困惑,为什么最终的梯度是各个时刻的梯度之和呢?我们前面只是直接用了这个结论,实际上这里面是有道理的,只是这个数学推导比较绕脑子。感兴趣的同学可以仔细阅读接下来这一段,它用到了矩阵对矩阵求导、张量与向量相乘运算的一些法则。
式5推导
我们还是从这个式子开始:
\(net_t=UX_t+Wf(net_{t-1})\)
因为\(UX_t\)与\(W\)完全无关,我们把它看作常量。现在,考虑第一个式子加号右边的部分,因为\(W\)和\(f(net_{t-1})\)都是\(W\)的函数,因此我们要用到大学里学过的复合函数求导方法:
\((uv)'=u'v+uv'\)
因此,上面的式子写成:
\(\frac{\partial net_t}{\partial W}=\frac{\partial W}{\partial W}f(net_{t-1})+W\frac{\partial f(net_{t-1})}{\partial W}\)
我们最终需要计算的是\(\nabla_WE\):
$$\begin{aligned}\nabla_WE &=\frac{\partial E}{\partial W} \
&=\frac{\partial E}{\partial net_t}\frac{\partial net_t}{\partial W} \
&=\delta_t^T\frac{\partial W}{\partial W}f(net_{t-1})+\delta_t^TW\frac{\partial f(net_{t-1})}{\partial W}
\end{aligned} \tag{6}$$先计算式6加号左边部分。\(\frac{\partial W}{\partial W}\)是矩阵对矩阵求导,其结果是一个四维张量(tensor):
$$\begin{aligned}\frac{\partial W}{\partial W} &=\left[ \begin{matrix} \frac{\partial w_{11}}{\partial W} & \frac{\partial w_{12}}{\partial W} & \cdots & \frac{\partial w_{1n}}{\partial W} \ \frac{\partial w_{21}}{\partial W} & \frac{\partial w_{22}}{\partial W} & \cdots & \frac{\partial w_{2n}}{\partial W} \ \vdots & \vdots & \ddots & \vdots \ \frac{\partial w_{n1}}{\partial W} & \frac{\partial w_{n2}}{\partial W} & \cdots & \frac{\partial w_{nn}}{\partial W} \end{matrix} \right] \
&=\left[\begin{matrix}\left[ \begin{matrix} \frac{\partial w_{11}}{\partial w_{11}} & \frac{\partial w_{11}}{\partial w_{12}} & \cdots & \frac{\partial w_{11}}{\partial w_{1n}} \ \frac{\partial w_{11}}{\partial w_{21}} & \frac{\partial w_{11}}{\partial w_{22}} & \cdots & \frac{\partial w_{11}}{\partial w_{2n}} \ \vdots & \vdots & \ddots & \vdots \ \frac{\partial w_{11}}{\partial w_{n1}} & \frac{\partial w_{11}}{\partial w_{n2}} & \cdots & \frac{\partial w_{11}}{\partial w_{nn}} \end{matrix} \right] & \left[ \begin{matrix} \frac{\partial w_{12}}{\partial w_{11}} & \frac{\partial w_{12}}{\partial w_{12}} & \cdots & \frac{\partial w_{12}}{\partial w_{1n}} \ \frac{\partial w_{12}}{\partial w_{21}} & \frac{\partial w_{12}}{\partial w_{22}} & \cdots & \frac{\partial w_{12}}{\partial w_{2n}} \ \vdots & \vdots & \ddots & \vdots \ \frac{\partial w_{12}}{\partial w_{n1}} & \frac{\partial w_{12}}{\partial w_{n2}} & \cdots & \frac{\partial w_{12}}{\partial w_{nn}} \end{matrix} \right] \cdots \ \vdots & \vdots
\end{matrix} \right] \ &=\left[\begin{matrix}\left[ \begin{matrix} 1 & 0 & \cdots & 0 \ 0 & 0 & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & 0 \end{matrix} \right] & \left[ \begin{matrix} 0 & 1 & \cdots & 0 \ 0 & 0 & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & 0 \end{matrix} \right] \cdots \ \vdots & \vdots \end{matrix} \right]
\end{aligned} $$接下来,我们知道\(S_{t-1}=f(net_{t-1})\),它是一个列向量。让上面的四维张量与这个向量相乘,得到一个三维张量,再左乘行向量\(\delta_t^T\),最终得到一个矩阵:
$$\begin{aligned}\delta_t^T\frac{\partial W}{\partial W}f(net_{t-1}) &=\delta_t^T\frac{\partial E}{\partial W}S_{t-1} \
&=\delta_t^T \left[\begin{matrix}\left[ \begin{matrix} 1 & 0 & \cdots & 0 \ 0 & 0 & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & 0 \end{matrix} \right] & \left[ \begin{matrix} 0 & 1 & \cdots & 0 \ 0 & 0 & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & 0 \end{matrix} \right] \cdots \ \vdots & \vdots \end{matrix} \right] \left[ \begin{matrix} s_1^{t-1} \ s_2^{t-1} \ \vdots \ s_n^{t-1} \end{matrix} \right] \
&=\delta_t^T \left[\begin{matrix}\left[ \begin{matrix} s_1^{t-1} \ 0 \ \vdots \ 0 \end{matrix} \right] & \left[ \begin{matrix} s_2^{t-1} \ 0 \ \vdots \ 0 \end{matrix} \right] \cdots \ \vdots & \vdots \end{matrix} \right] \
&= \left[ \begin{matrix}\delta_1^t & \delta_2^t & \cdots & \delta_n^t \end{matrix} \right]\left[\begin{matrix}\left[ \begin{matrix} s_1^{t-1} \ 0 \ \vdots \ 0 \end{matrix} \right] & \left[ \begin{matrix} s_2^{t-1} \ 0 \ \vdots \ 0 \end{matrix} \right] \cdots \ \vdots & \vdots \end{matrix} \right] \
&=\left[ \begin{matrix} \delta_1ts_1 & \delta_1ts_2 & \cdots & \delta_1ts_n \ \delta_2ts_1 & \delta_2ts_2 & \cdots & \delta_2ts_n \ \vdots & \vdots & \ddots & \vdots \ \delta_nts_1 & \delta_nts_2 & \cdots & \delta_nts_n \end{matrix} \right] \
&=\nabla_{W_t}E
\end{aligned} $$先计算式6加号右边部分
\[\begin{aligned}\delta_t^TW\frac{\partial f(net_{t-1})}{\partial W} &=\delta_t^TW\frac{\partial f(net_{t-1})}{\partial net_{t-1}}\frac{\partial net_{t-1}}{\partial W} \\ &=\delta_t^T Wf'(net_{t-1})\frac{\partial net_{t-1}}{\partial W} \\ &=\delta_t^T\frac{\partial net_t}{\partial net_{t-1}}\frac{\partial net_{t-1}}{\partial W} \\ &=\delta_{t-1}^T\frac{\partial net_{t-1}}{\partial W} \end{aligned} \]于是,我们得到了如下递推公式:
$$\begin{aligned}\nabla_WE &=\frac{\partial E}{\partial W} \
&=\frac{\partial E}{\partial net_t}\frac{\partial net_t}{\partial W} \
&=\nabla_{W_t}E+\delta_{t-1}^T\frac{\partial net_{t-1}}{\partial W} \
&=\nabla_{W_t}E+\nabla_{W_{t-1}}E+\delta_{t-2}^T\frac{\partial net_{t-2}}{\partial W} \
&=\nabla_{W_t}E+\nabla_{W_{t-1}}E+\cdots+\nabla_{W_1}E \
&=\Sigma_{k=1}^t \nabla_{W_k}E
\end{aligned}$$以上过程证明了:最终的梯度\(\nabla_WE\)是各个时刻的梯度之和。
同权重矩阵\(W\)类似,我们可以得到权重矩阵\(U\)的计算方法:
$$\begin{aligned}\nabla_{U_t}E &=\left[ \begin{matrix} \delta_1tx_1t & \delta_1tx_2t & \cdots & \delta_1tx_mt \ \delta_2tx_1t & \delta_2tx_2t & \cdots & \delta_2tx_mt \ \vdots & \vdots & \ddots & \vdots \ \delta_ntx_1t & \delta_nts_2t & \cdots & \delta_ntx_mt \end{matrix} \right] \end{aligned} $$
上式是误差函数\(E\)在\(t\)时刻对权重矩阵\(U\)的梯度。和权重矩阵\(W\)一样,最终的梯度也是各个时刻的梯度之和:
\(\nabla_UE=\Sigma_{i=1}^t\nabla_{U_i}E\)
具体证明不再赘述,感兴趣的同学可以练习推导。
1.3.2 \(RNN\)的梯度爆炸和消失问题
不幸的是,实践中前面介绍的几种\(RNNs\)并不能很好的处理较长的序列。纳尼?!这不是和前面说的矛盾吗,前面不是说能任意长么,大家可以回头看一眼,前面说的是[理论上]可以任意上,现实和理想还是有一定距离的。一个主要的原因是,\(RNN\)在训练中很容易发生梯度爆炸和梯度消失,这导致训练时梯度不能在较长序列中一直传递下去,从而使\(RNN\)无法捕捉到长距离的影响。
为什么\(RNN\)会产生梯度爆炸和消失呢?我们接下来将详细分析一下原因。我们根据式3可得:
\(\delta_k^T=\delta_t^T\prod_{i=k}^{t-1}Wdiag[f'(net_i)]\)
$$\begin{aligned} \parallel \delta_k^T \parallel &\leq \parallel \delta_t^T \parallel \prod_{i=k}^{t-1}\parallel W \parallel \parallel diag[f'(net_i)] \parallel \
&\leq \parallel \delta_t^T \parallel(\beta_W\beta_f)^{t-k}
\end{aligned} $$
上式的\(\beta\)定义为矩阵的摸的上界。因为上式是一个指数函数,如果\(t-k\)很大的话(也就是向前看很远的时候),会导致对应的误差项的值增长或缩小得非常快,这样就会导致相应的梯度爆炸和梯度消失问题(取决于\(\beta\)大于1还是小于1)。
通常来说,梯度爆炸更容易处理一些。因为梯度爆炸的时候,运行代码会收到\(NaN\)错误。我们也可以设置一个梯度阈值,当梯度超过这个阈值的时候可以直接截取。
梯度消失更难检测,而且也更难处理一些。总的来说,我们有三种方法应对梯度消失问题:
- 1.合理的初始化权重值。初始化权重,使每个神经元尽可能不要取极大或极小值,以避开梯度消失的区域;
- 2.使用\(relu\)代替\(sigmoid\)和\(tanh\)作为激活函数。原理之前的文章里已有所提及;
- 3.使用其他结构的\(RNNs\),比如长短时记忆网络(LSTM)和Gated Recurrent Unit(GRU),这是最流行的网络结构。我们将在后续内容介绍这两种网络。
1.4 \(RNN\)的应用举例——基于\(RNN\)的语言模型
现在,引入一个例子,开篇提过的语言模型,不过现在是基于\(RNN\)的语言模型。我们首先把词依次输入到循环神经网络中,每输入一个词,循环神经网络就输出截止目前为止,下一个最有可能的词。如,当我们依次输入:
我 昨天 上学 迟到 了
神经网络的输出如下图所示:

图中,\(s\)和\(e\)是两个特殊的词,分别表示一个序列的开始和结束。
神经网络的输入和输出都是向量,为了让语言模型能够被神经网络处理,我们必须把词表达为向量的形式,这样神经网络才能处理它。
1.4.1 向量化
神经网络的输入是词,我们可以用以下步骤对输入进行向量化:
1.建立一个包含所有词的词典,每个词在词典里面有一个唯一的编号;
2.任意一个词都可以用一个\(N\)维的\(one-hot\)向量来表示。其中,\(N\)是词典中包含的词的个数。假设一个词在词典中的编号是\(i\),\(v\)是这个词的向量,\(v_j\)是向量的第\(j\)元素,则:
$$v_j= \begin{cases}
1 && j=i\
0 && j\neq i\
\end{cases}$$
上面这个公式的含义,可以用下面的图来直观的表示:
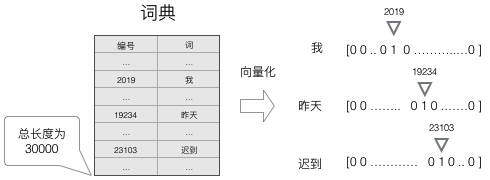
使用这种向量化方法,我们就得到了一个高维、稀疏的向量(稀疏是指绝大部分元素的值都是0)。处理这样的向量会导致我们的神经网络有很多的参数,带来庞大的计算量。因此,往往会需要使用一些降维方法,将高维的稀疏向量转变为低维的稠密向量。
不过这个话题我们就不再这篇文章中讨论了。
语言模型要求的输出是下一个最可能的词,我们可以让循环神经网络计算计算词典中每个词是下一个词的概率,这样,概率最大的词就是下一个最可能的词。因此,神经网络的输出向量也是一个\(N\)维向量,向量中的每个元素对应着词典中相应的词是下一个词的概率。如下图所示:
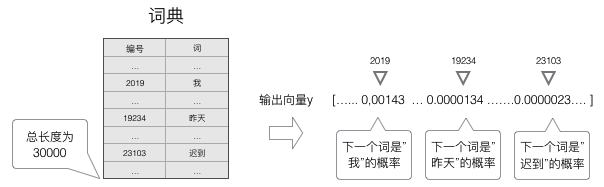
前面提到,语言模型是对下一个词出现的概率进行建模。那么,怎样让神经网络输出概率呢?方法就是用\(softmax\)层作为神经网络的输出层。
1.4.2 \(Softmax\)层
我们先来看一下\(softmax\)函数的定义:
\(g(z_i)=\frac{e^{z_i}}{\Sigma_ke^{z_k}}\)
这个公式看起来可能很晕,举例说明一下,\(Softmax\)层如下图所示:

从上图我们可以看到,\(Softmax\) \(layer\)的输入是一个向量,输出也是一个向量,两个向量的维度是一样的(在这个例子里面是4)。输入向量x=[1 2 3 4]经过\(softmax\)层之后,经过上面的\(softmax\)函数计算,转变为输出向量y=[0.03 0.09 0.24 0.64]。计算过程为:
\(y_1=\frac{e^{x_1}}{\Sigma_ke^{x_k}}=\frac{e^1}{e^1+e^2+e^3+e^4}=0.03\)
\(y_2=\frac{e^2}{e^1+e^2+e^3+e^4}=0.09\)
\(y_3=\frac{e^3}{e^1+e^2+e^3+e^4}=0.24\)
\(y_4=\frac{e^4}{e^1+e^2+e^3+e^4}=0.64\)
总结一下输出向量\(y\)的特征:
1.每一项为取值为0-1之间的正数;
2.所有项的总和为1。
不难发现,这些特征和概率的特征是一样的,因此我们可以把它们看做是概率。对于语言模型来说,我们可以认为模型预测下一个词是词典中第一个词的概率是0.03,是词典中第二个词的概率是0.09,以此类推。
1.4.3 语言模型的训练
可以使用监督学习的方法对语言模型进行训练,首先,需要准备训练数据集。接下来,我们介绍怎样把语料转换成语言模型的训练数据集。
我 昨天 上学 迟到 了
首先,我们获取输入-标签对:
| 输入 | 标签 |
|---|---|
| s | 我 |
| 我 | 昨天 |
| 昨天 | 上学 |
| 上学 | 迟到 |
| 迟到 | 了 |
| 了 | e |
然后,使用前面介绍过的向量化方法,对输入x和标签y进行向量化。这里面有意思的是,对标签y进行向量化,其结果也是一个one-hot向量。例如,我们对标签『我』进行向量化,得到的向量中,只有第2019个元素的值是1,其他位置的元素的值都是0。它的含义就是下一个词是『我』的概率是1,是其它词的概率都是0。
最后,我们使用交叉熵误差函数作为优化目标,对模型进行优化。
注:在实际工程中,我们可以使用大量的语料来对模型进行训练,获取训练数据和训练的方法都是相同的。
1.4.4 交叉熵误差
一般来说,当神经网络的输出层是\(Softmax\)层时,对应的误差函数E通常选择交叉熵误差函数,其定义如下:
\(L(y,o)=-\frac{1}{N}\Sigma_{n\in N}y_nlogo_n\)
在上式中,\(N\)是训练样本的个数,向量\(y_n\)是样本的标记,向量\(o_n\)是网络的输出。标记\(y_n\)是一个one-hot向量,例如\(y_1=[1,0,0,0]\),如果网络的输出\(o=[0.03,0.09,0.24,0.64]\),那么,交叉熵误差是(假设只有一个训练样本,即N=1):
$$\begin{aligned}L(y,o) &=-\frac{1}{N}\Sigma_{n\in N}y_nlogo_n \
&= -y_1logo_1 \
&= -(1log0.03+0log0.09+0log0.24+0log0.64) \
&= 3.51
\end{aligned} $$
我们当然可以选择其他函数作为我们的误差函数,比如最小平方误差函数(MSE)。不过对概率进行建模时,选择交叉熵误差函数更make sense。具体原因,感兴趣的读者请阅读参考文献5。
1.5 小结
上述文章中,我们介绍了循环神经网络以及它的训练算法。同时也介绍了循环神经网络很难训练的原因,这导致了它在实际应用中,很难处理长距离的依赖。在本部分,我们将介绍一种改进之后的循环神经网络:长短时记忆网络(\(LSTM\)),它成功的解决了原始循环神经网络的缺陷,成为当前最流行的\(RNN\),在语音识别、图片描述、自然语言处理等许多领域中成功应用。但不幸的一面是,\(LSTM\)的结构很复杂,因此,我们需要花上一些力气,才能把\(LSTM\)以及它的训练算法弄明白。在搞清楚\(LSTM\)之后,我们再介绍一种\(LSTM\)的变体:\(GRU\)。 它的结构比\(LSTM\)简单,而效果却和\(LSTM\)一样好,因此,它正在逐渐流行起来。
1.6 什么是\(LSTM\)网络?
1.6.1 普通\(RNN\)回顾
前述文中介绍了很多\(RNN\)的内容,涉及很多公式计算,该部分以图片形式简要回顾一下,普通\(RNN\)的主要形式如下图所示:

图中,
\(x\)为当前状态下数据的输入,\(h\)表示接收到的上一个节点的输入。
\(y\)为当前节点状态下的输出,而\(h'\)为传递到下一个节点的输出。
通过上图的公式可以看到,输出\(h'\)与\(x\)和\(h\)的值都相关。
而\(y\)则常常使用\(h'\)投入到一个线性层(主要是进行维度映射)然后使用\(softmax\)进行分类得到需要的数据。
对这里的\(y\)如何通过\(h'\)计算得到往往看具体模型的使用方式。
通过序列形式的输入,我们能够得到如下形式的\(RNN\):

1.6.2 \(LSTM\)-特殊的\(RNN\)
长短期记忆(\(LSTM\))是一种特殊的\(RNN\),主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说,就是相比普通的\(RNN\),\(LSTM\)能够在更长的序列中有更好的表现。
\(LSTM\)结构(图右)和普通\(RNN\)的主要输入输出区别如下所示。

相比\(RNN\)只有一个传递状态\(h^t\) ,\(LSTM\)有两个传输状态,一个\(c^t\) (cell state),和一个 \(h^t\)(hidden state)。(\(Tips:RNN\)中的\(h^t\)对于\(LSTM\)中的\(c^t\))
其中对于传递下去的\(c^t\)改变得很慢,通常输出的\(c^t\)是上一个状态传过来的\(c^{t-1}\)加上一些数值。
而\(h^t\)则在不同节点下往往会有很大的区别。
1.6.3 深入\(LSTM\)结构
下面具体对\(LSTM\)的内部结构来进行剖析。
首先使用\(LSTM\)的当前输入\(x^t\)和上一个状态传递下来的\(h^{t-1}\)拼接训练得到四个状态。


其中,\(z^f\),\(z^i\),\(z^o\)是由拼接向量乘以权重矩阵之后,再通过一个\(sigmoid\)激活函数转换成0到1之间的数值,来作为一种门控状态。而\(z\)则是将结果通过一个\(tanh\)激活函数将转换成-1到1之间的值(这里使用\(tanh\)是因为这里是将其做为输入数据,而不是门控信号)。
下面开始进一步介绍这四个状态在\(LSTM\)内部的使用:

注:\(\odot\)是Hadamard Product,也就是操作矩阵中对应的元素相乘,因此要求两个相乘矩阵是同型的。\(\oplus\)则代表进行矩阵加法。
\(LSTM\)内部主要有三个阶段:
-
忘记阶段。这个阶段主要是对上一个节点传进来的输入进行选择性忘记。简单来说就是会 “忘记不重要的,记住重要的”。具体来说是通过计算得到的\(z^f\)(\(f\)表示\(forget\))来作为忘记门控,来控制上一个状态的\(c^{t-1}\)哪些需要留哪些需要忘。
-
选择记忆阶段。这个阶段将这个阶段的输入有选择性地进行“记忆”。主要是会对输入 \(x^t\)进行选择记忆。哪些重要则着重记录下来,哪些不重要,则少记一些。当前的输入内容由前面计算得到的表\(z\)示。而选择的门控信号则是由\(z^i\)(\(i\)代表\(information\))来进行控制。
将上面两步得到的结果相加,即可得到传输给下一个状态的\(c^t\)。也就是上图中的第一个公式。
- 输出阶段。这个阶段将决定哪些将会被当成当前状态的输出。主要是通过\(z^o\)来进行控制的。并且还对上一阶段得到进的\(c^o\)(通过一个\(tanh\)激活函数进行变化)。
与普通\(RNN\)类似,输出\(y^t\)往往最终也是通过\(h^t\)变化得到。
1.6.4 小结
以上,就是\(LSTM\)的内部结构。通过门控状态来控制传输状态,记住需要长时间记忆的,忘记不重要的信息;而不像普通的\(RNN\)那样只能够“呆萌”地仅有一种记忆叠加方式。对很多需要“长期记忆”的任务来说,尤其好用。
但也因为引入了很多内容,导致参数变多,也使得训练难度加大了很多。因此很多时候我们往往会使用效果和\(LSTM\)相当但参数更少的\(GRU\)来构建大训练量的模型。
1.7 什么是\(GRU\)网络?
1.7.1 为什么需要\(GRU\)?
\(GRU\)(\(Gate Recurrent Unit\))是\(RNN\)的一种。和\(LSTM\)一样,也是为了解决长期记忆和反向传播中的梯度等问题而提出来的。
\(GRU\)和\(LSTM\)在很多情况下实际表现上相差无几,那么为什么我们要使用新人\(GRU\)(2014年提出)而不是相对经受了更多考验的\(LSTM\)(1997提出)呢?
引用论文中的一段话来说明\(GRU\)的优势所在:

我们在我们的实验中选择\(GRU\)是因为它的实验效果与\(LSTM\)相似,但是更易于计算。
简单来说就是贫穷限制了我们的计算能力...
相比\(LSTM\),使用\(GRU\)能够达到相当的效果,并且相比之下更容易进行训练,能够很大程度上提高训练效率,因此很多时候会更倾向于使用\(GRU\)。
OK,那么为什么说\(GRU\)更容易进行训练呢,下面开始介绍一下\(GRU\)的内部结构。
1.7.2 \(GRU\)的输入输出结构
\(GRU\)的输入输出结构与普通的\(RNN\)是一样的,如下图所示:

有一个当前的输入\(x^t\),和上一个节点传递下来的隐状态\(h^{t-1}\)(hidden state)),这个隐状态包含了之前节点的相关信息。
结合\(x^t\)和\(h^{t-1}\),\(GRU\)会得到当前隐藏节点的输出\(y^t\)和传递给下一个节点的隐状态\(h^t\)。
那么,\(GRU\)到底有什么特别之处呢?下面来对它的内部结构进行分析!
1.7.3 \(GRU\)的内部结构
\(GRU\)的内部结构如下图所示:

注:\(\odot\)是Hadamard Product,也就是操作矩阵中对应的元素相乘,因此要求两个相乘矩阵是同型的。\(\oplus\)则代表进行矩阵加法。
首先,我们先通过上一个传输下来的状态\(h^{t-1}\)和当前节点的输入\(x^t\)来获取两个门控状态。如下图,其中\(r\)控制重置的门控(reset gate),\(z\)为控制更新的门控(update gate)。

Tips:\(\delta\)为\(sigmoid\)函数,通过这个函数可以将数据变换为0-1范围内的数值,从而来充当门控信号。
与\(LSTM\)分明的层次结构不同,下面将对\(GRU\)进行一气呵成的介绍~~~ 请大家屏住呼吸,不要眨眼。
得到门控信号之后,首先使用重置门控来得到“重置”之后的数据\(h'^{t-1}=h^{t-1}\odot r\) ,再将 \(h'^{t-1}\)与输入\(x^t\)进行拼接,再通过一个\(tanh\)激活函数来将数据放缩到-1~1的范围内。即得到如下图所示的\(h'\)。

这里的\(h'\)主要是包含了当前输入的\(x^t\)数据。有针对性地对\(h'\)添加到当前的隐藏状态,相当于“记忆了当前时刻的状态”,类似于LSTM的选择记忆阶段 。
最后介绍\(GRU\)最关键的一个步骤,我们可以称之为”更新记忆“阶段。
在这个阶段,我们同时进行了遗忘了记忆两个步骤。我们使用了先前得到的更新门控\(z\)(update gate)。
更新表达式:\(h^t=z\odot h^{t-1}+(1-z)\odot h'\)
首先再次强调一下,门控信号(这里的\(z\))的范围为0~1。门控信号越接近1,代表“记忆”下来的数据越多;而越接近0则代表“遗忘”的越多。
\(GRU\)很聪明的一点就在于,我们使用了同一个门控\(z\)就同时可以进行遗忘和选择记忆(\(LSTM\)则要使用多个门控)。
- \(z\odot h^{t-1}\) :表示对原本隐藏状态的选择性“遗忘”。这里的\(z\)可以想象成遗忘门(forget gate),忘记\(h^{t-1}\)维度中一些不重要的信息。
- \((1-z)\odot h'\) : 表示对包含当前节点信息的进\(h'\)行选择性“记忆”。与上面类似,这里的\((1-z)\)同理会忘记\(h'\)维度中的一些不重要的信息。或者,这里我们更应当看做是对\(h'\)维度中的某些信息进行选择。
- \(h^t=z\odot h^{t-1}+(1-z)\odot h'\) :结合上述,这一步的操作就是忘记传递下来的\(h^{t-1}\)中的某些维度信息,并加入当前节点输入的某些维度信息。
可以看到,这里的遗忘\(z\)和选择是\((1-z)\)联动的。也就是说,对于传递进来的维度信息,我们会进行选择性遗忘,即遗忘了多少权重\((z)\),我们就会使用包含当前输入的 \(h'\)中所对应的权重进行弥补\((1-z)\)。以保持一种”恒定“状态。
1.7.4 \(LSTM\)与\(GRU\)的关系
\(GRU\)是在2014年提出来的,而\(LSTM\)是1997年。它们的提出都是为了解决相似的问题,那么\(GRU\)难免会参考\(LSTM\)的内部结构。那么他们之间的关系大概是怎么样的呢?这里简单介绍一下。
大家看到\(r\)(reset gate)实际上与它的名字有点不符。我们仅仅使用它来获得了\(h'\)。
那么这里的\(h'\)实际上可以看成对应于\(LSTM\)中的hidden state;上一个节点传下来的则\(h^{t-1}\)对应于\(LSTM\)中的cell state。\(z\)对应的则是\(LSTM\)中的\(z^f\) forget gate,那么我\((1-z)\)们似乎就可以看成是选择门\(z^i\)了。
1.7.5 小结
\(GRU\)输入输出的结构与普通的\(RNN\)相似,其中的内部思想与\(LSTM\)相似。
与\(LSTM\)相比,\(GRU\)内部少了一个”门控“,参数比\(LSTM\)少,但是却也能够达到与\(LSTM\)相当的功能。考虑到硬件的计算能力和时间成本,因而很多时候我们也就会选择更加“实用”的\(GRU\)。
声明
本博客所有内容仅供学习,不为商用,如有侵权,请联系博主,谢谢。
参考文献
[1] 李宏毅,Deep Learning Tutorial,2018
[2] \(RNN\): https://zybuluo.com/hanbingtao/note/541458
[3] \(LSTM\): https://zhuanlan.zhihu.com/p/32085405




 浙公网安备 33010602011771号
浙公网安备 33010602011771号