【二维前缀和与差分】LeetCode 2536. 子矩阵元素加 1

题目

https://leetcode.cn/problems/increment-submatrices-by-one/description/

题解

这是一道二维差分的典题，但是为了实现二维差分，我们首先需要掌握前置知识二维前缀和。接下来我先向大家介绍二维前缀和的意义、定义和用法：

二维前缀和的意义

假设存在一个 \(n \times m\) 的整数矩阵，你需要询问 \(q\) 次子矩阵内的整数和。朴素算法的最差时间复杂度是 \(O(qnm)\)，当 \(n, m\) 都十分巨大时，显然是不可接受的。那么我们就需要一个能够快速出一个区域内的元素和（也可以非加法，但需要是可逆运算）的算法，此时二维前缀和算法就起到了作用。

二维前缀和的定义

我们定义一个新的矩阵 \(prefix\)，其中 \(prefix[i][j]\) 表示从原始矩阵 \(matrix[0][0]\) 到 \(matrix[i][j]\) 这个矩形区域内所有元素的总和。

形式化定义：$$prefix[i][j] = sum(matrix[x][y])，0 <= x <= i, 0 <= y <= j。$$

我们最终要构建的就是这样一个 \(prefix\) 矩阵。

问：能使用二维前缀和算法的矩阵需要满足什么性质？
二维前缀和算法实际上是在一个阿贝尔群（交换群）上的运算，因此核心要求是具备可逆的群运算，具体来说需要满足：

1. 结合律：\((a ∘ b) ∘ c = a ∘ (b ∘ c)\)
2. 存在单位元：存在元素 \(e\) 使得 \(a ∘ e = e ∘ a = a\)
3. 存在逆元：对于每个 \(a\)，存在 \(a'\) 使得 \(a ∘ a' = e\)

为什么需要满足上述性质？

• 结合律：确保前缀计算的正确性
• 单位元：用于初始化前缀数组（\(prefix[0][j]\) 和 \(prefix[i][0]\) 设为单位元）
• 逆元：用于从大区域中"减去"不需要的部分

常见运算：

运算	结合律	单位元	逆元	是否适用
加法	✓	0	-a	✓
异或	✓	0	a自身	✓
乘法	✓	1	1/a	✓（但注意除0问题）
矩阵乘法	✓	单位矩阵	逆矩阵	✓（但非交换）
最大值	✓	-∞	无逆元	✗
最小值	✓	+∞	无逆元	✗

阿贝尔群 = 群 + 交换律

设运算为 ∘，逆运算为 ∘⁻¹，那么：
构建公式：$$prefix[i][j] = prefix[i-1][j] ∘ prefix[i][j-1] ∘ prefix[i-1][j-1]^{-1} ∘ matrix[i-1][j-1]$$
查询公式：$$result = prefix[r_2+1][c_2+1] ∘ prefix[r_1][c_2+1]^{-1} ∘ prefix[r_2+1][c_1]^{-1} ∘ prefix[r_1][c_1]$$
对于加法群：∘ 是 +，逆是 -
对于异或群：∘ 是 ⊕，逆是 ⊕（自逆）
对于乘法群：∘ 是 ×，逆是 ÷

二维前缀和的用法

下图出自灵茶山艾府的题解：https://leetcode.cn/problems/increment-submatrices-by-one/solutions/2062756/er-wei-chai-fen-by-endlesscheng-mh0h/?envType=daily-question&envId=2025-11-14
如何构建二维前缀和矩阵？
构建二维前缀和矩阵需要使用动态规划的思想，关键点在于找到 \(prefix[i][j]\) 与之前已经计算过的前缀和之间的关系。观察下图，\(prefix[i][j]\) 的面积（总和）可以看作由四个部分组合而成：

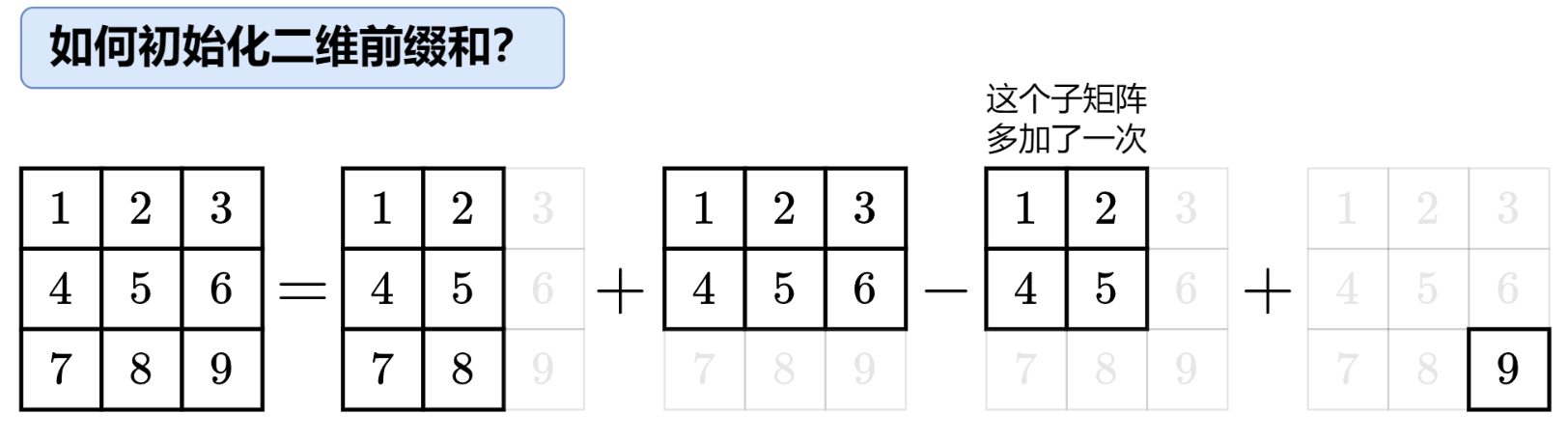
可以把它分解为：

1. 从 \((0, 0)\) 到 \((i-1, j)\) 的区域 A，其和为 \(prefix[i-1][j]\)
2. 从 \((0, 0)\) 到 \((i, j-1)\) 的区域 B，其和为 \(prefix[i][j-1]\)
3. 从 \((0, 0)\) 到 \((i-1, j-1)\) 的区域 C，其和为 \(prefix[i-1][j-1]\)
4. 当前格子 \((i, j)\) 本身的值 \(matrix[i][j]\)

把它们加起来，得到核心递推公式：$$prefix[i][j] = (A) + (B) + (C) + matrix[i][j] = prefix[i-1][j] + prefix[i][j-1] - prefix[i-1][j-1] + matrix[i][j]$$

边界处理：为了让这个公式对 \(i=0\) 或 \(j=0\) 也成立，我们通常会将 \(prefix\) 矩阵的尺寸设置为 \((n+1) \times (m+1)\)，即比原矩阵多一行一列，并且 \(prefix[0][j]\) 和 \(prefix[i][0]\) 都初始化为 \(0\)。这样，我们实际计算的是 \(prefix[1..n][1..m]\)，对应原矩阵的 \(matrix[0..n-1][0..m-1]\)。

如何使用二维前缀和进行区域运算查询？
现在我们已经有了 \(prefix\) 矩阵。假设我们要查询原矩阵中从 \((r_1, c_1)\) 到 \((r_2, c_2)\) 的矩形区域和（包含边界）。观察下图，矩形区域和的面积（总和）可以看作由四个部分组合而成：

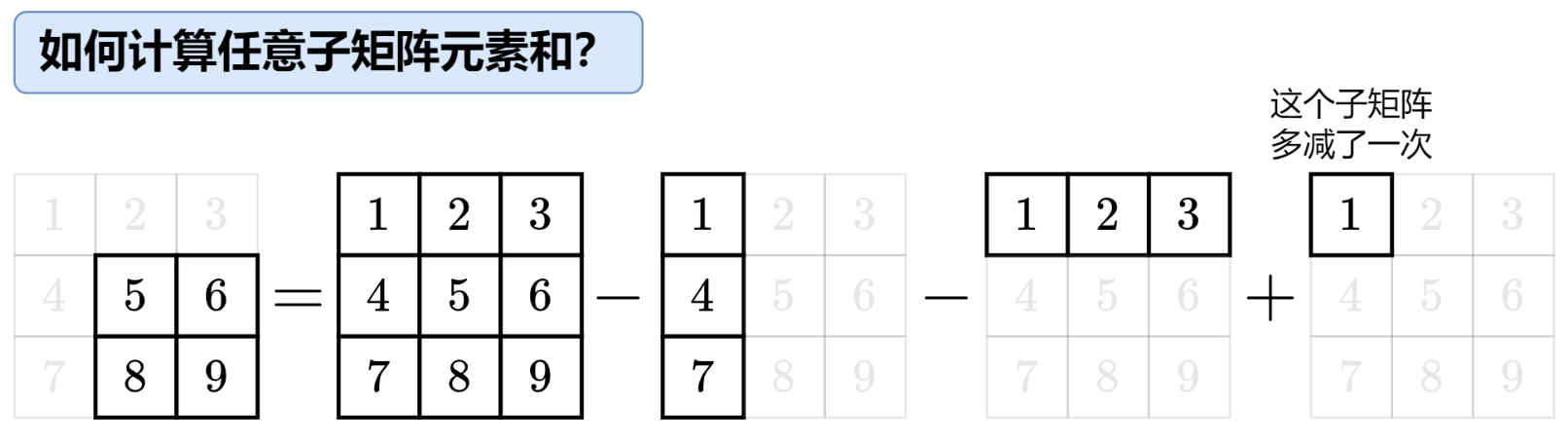
首先，我们得到从 \((0, 0)\) 到 \((r_2, c_2)\) 的总和 \(prefix[r_2+1][c_2+1]\)。（因为 \(prefix\) 矩阵下标比原矩阵大 \(1\)）
然后，减去上面不需要的区域 \(prefix[r_1][c_2+1]\)
再减去左边不需要的区域 \(prefix[r_2+1][c_1]\)
注意，左上角的区域被减了两次，所以需要加回来一次 \(prefix[r_1][c_1]\)

查询公式：$$sum_region(r_1, c_1, r_2, c_2) = prefix[r_2+1][c_2+1] - prefix[r_1][c_2+1] - prefix[r_2+1][c_1] + prefix[r_1][c_1]$$

二维差分的意义

场景：你有一个矩阵，需要频繁进行以下操作："给一个矩形区域内的所有元素都加上一个常数 \(k\)"。朴素算法是每次操作都遍历这个矩形区域，给每个元素加上 \(k\)，假设更新操作共 \(q\) 次，最差时间复杂度是 \(O(qnm)\)，显然无法接受。那么我们就需要一个能够快速更新一个子矩阵内的全部元素（执行操作要相同，比如都是加上 \(k\)）的算法，此时二维差分算法就起到了作用。

二维差分的定义

二维差分是二维前缀和的逆运算，也是一种非常重要的预处理技巧。它可以在 \(O(1)\) 时间内完成一次区域更新，最后通过一次 \(O(n \times m)\) 的前缀和计算得到最终矩阵。

二维差分的用法

在掌握了二维前缀和算法的前提下，观察下图可以了解从一维差分到二维差分的思想：

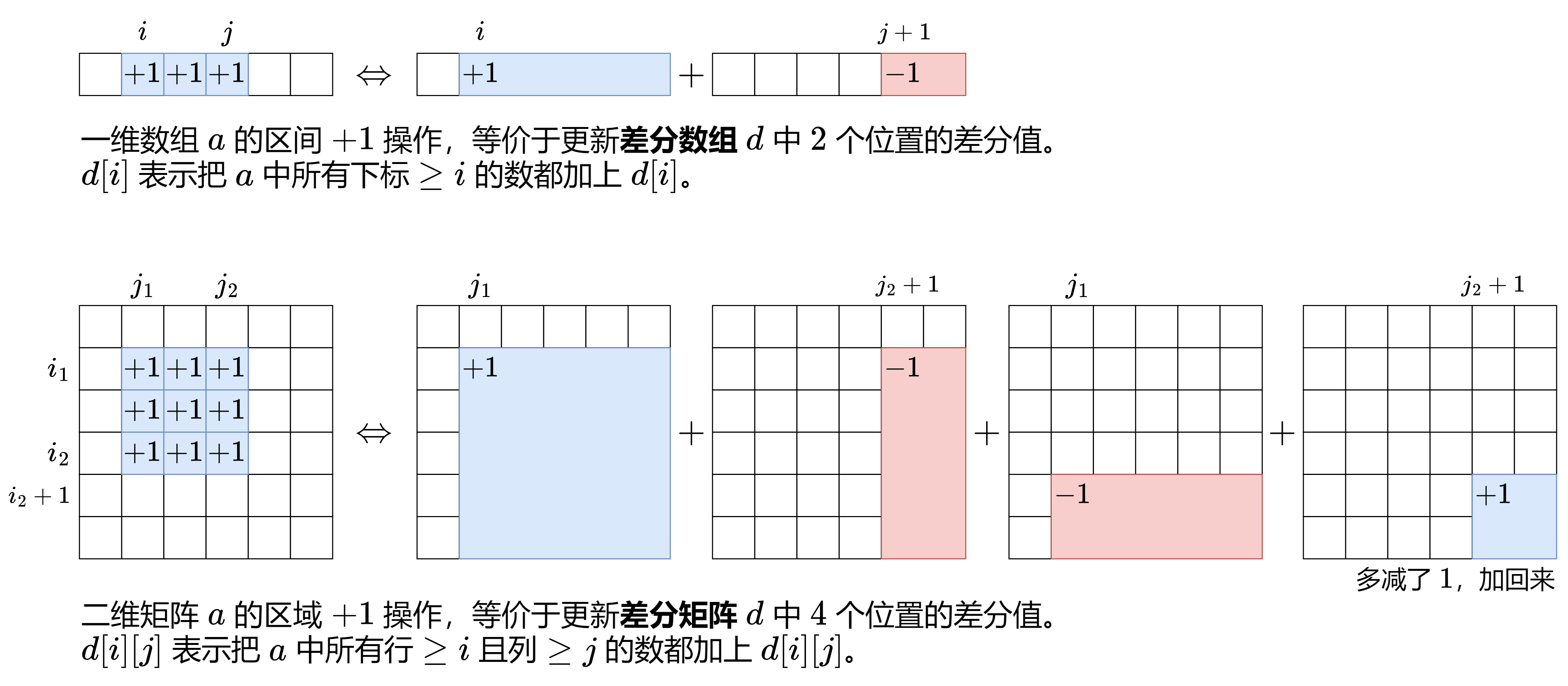
更新步骤：

1. \(diff[r_1][c_1] += k：从 (r1, c1) 开始的所有区域都会加上 k\)
2. \(diff[r_1][c_2+1] -= k：取消从 (r_1, c_2+1) 开始的右侧区域多加的 k\)
3. \(diff[r_2+1][c_1] -= k：取消从 (r_2+1, c_1) 开始的下侧区域多加的 k\)
4. \(diff[r_2+1][c_2+1] += k：右下角区域被减了两次，加回来一次\)

参考代码

class Solution {
public:
    vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {
        vector df(n + 2, vector<int>(n + 2));//二维差分数组
        vector ans(n, vector<int>(n));//答案数组（二维）

        for (auto &q: queries) {
            int& l1 = q[0], r1 = q[1], l2 = q[2], r2 = q[3];
            df[l1 + 1][r1 + 1] ++;//左上角+1
            df[l1 + 1][r2 + 2] --;//右上角-1
            df[l2 + 2][r1 + 1] --;//左下角+1
            df[l2 + 2][r2 + 2] ++;//右下角-1
        }

        for (int i = 1; i <= n; ++ i) {
            for (int j = 1; j <= n; ++ j) {
                df[i][j] += df[i - 1][j] + df[i][j - 1] - df[i - 1][j - 1];//求二维前缀和
                ans[i - 1][j - 1] = df[i][j];//存储答案
            }
        }

        return ans;
    }
};