【前缀和+差分+二分】LeetCode 2528. 最大化城市的最小电量

题目

https://leetcode.cn/problems/maximize-the-minimum-powered-city/description/

题解

以stations = [1,2,4,5,0], r = 1, k = 2为测试用例进行讲解，从第 1 座城市到第 5 座城市对各个城市的电量影响如下图所示：

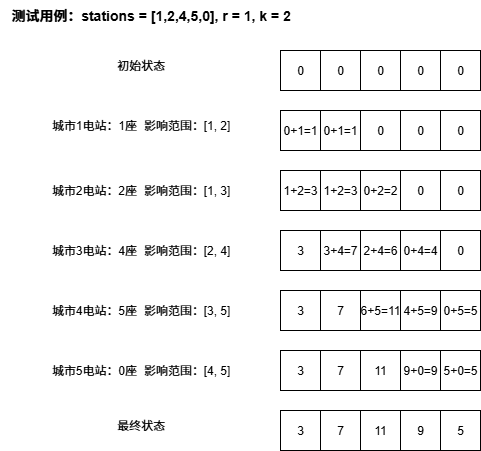
由上图，我们可以知晓题目大致的一个执行逻辑。但当 \(n\) 和 \(r\) 都非常巨大的时候，朴素的为每个城市的电站能影响到城市进行电量更新，时间复杂度达到 \(O(n^2)\) 从而具有 TLE 的风险。合理的做法是使用差分数组，从而每次都做到 \(O(1)\) 时间复杂度更新，最后使用一趟前缀和完成计算，总体时间复杂度为 \(O(n)\)。差分数组的逻辑如下图所示：

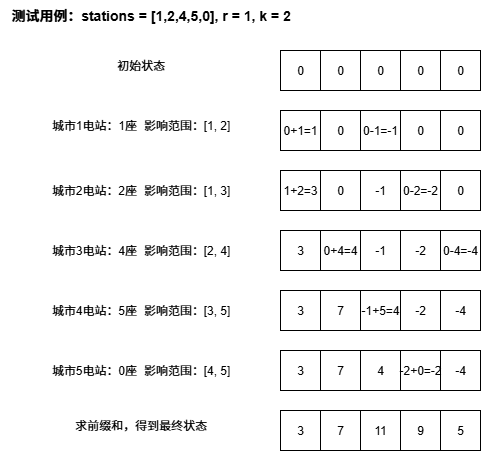
分析至此，已经学会了如何使用前缀和与差分维护出该题没有额外的供电站，即 \(k = 0\) 的场景。

若题目能使用的供电站数量是无限制的，且题目要求是让每个城市都有大于 \(0\) 的电量，可以参考相似题目《GuatOJ 烟雾报警器》：
http://oj.hhzzss.cn/problem/15-O1-E

对于一段电量都是 \(0\) 的城市 \([left, right]\)，若想使得这段都至少电量为 \(1\)，建站的贪心思路是在 \(min(left + r, right)\) 的位置建一个供电站，此时 \([left, min(left + 2 \times r, right)]\) 就都满足电量至少为 \(1\)；然后若 \(left + 2 \times r < right\) 成立，就再于 \(left + 3 \times r\) 的位置建立一个供电站，反复该操作，直至 \([left, right]\) 都满足电量至少为 \(1\)。根据该思路，就可以解决《GuatOJ 烟雾报警器》这道题。

如果说对 \(k\) 的大小有了限制，想问所有城市最少的电量最大是多少，就演变成了今天的这道题。建立在做出了《烟雾报警器》的基础之上，我们知道了让每座城市的电量都至少为 \(1\) 的做法。那么在 \(k\) 大小有限制的情况下，我们是不是也能用朴素算法去计算出所有城市最少的电量最大值 \(ans\) 能是多少？朴素算法的思路为从 \(1\) 开始枚举 \(ans\) 的大小，每次将 \(ans\) 的大小递增 \(1\)，直至超出 \(k\) 所限制的范围。

对于上述的过程，我们一定能找到一个上确界 \(ans'\) 满足：若想使得所有城市最少的电量的最大值满足大于等于 \(ans'\)，需要使用的供电站数量会大于 \(k\)。

在上确界 \(ans'\) 左边的每个值都是可以达到的，在上确界 \(ans'\) 及右边的每个值都是不可以达到的。那么对于该过程就可以使用二分法进行维护，最终维护出上确界。

时间复杂度：\(O(nlogU)\)
空间复杂度：\(O(n)\)

参考代码

GuatOJ 烟雾报警器

#include<bits/stdc++.h>
using namespace std;

constexpr int N = 5e5 + 7;
int diff[N];//差分数组
int n, m, k, x, ans;

int main() {
    ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
    cin >> n >> m >> k;
    for (int i = 0; i < m; ++ i) {
        cin >> x;//输入报警器位置
        int l = max(1, x - k);//位置为 x 的报警器能监测的在数轴上的左边界
        int r = min(n, x + k);//位置为 x 的报警器能监测的在数轴上的右边界
        diff[l] ++;//维护差分数组左端
        diff[r + 1] --;//维护差分数组右端
    }

    // 维护出差分数组
    for (int i = 1; i <= n; ++ i) {
        diff[i] += diff[i - 1];
        if (!diff[i]) {//位置 i 未被烟雾报警器监测到
            ++ ans;//使用的烟雾报警器数量 + 1
            //下列代码本质是在位置 min(i + k, n) 的位置放置一个烟雾报警器
            diff[i] ++;
            diff[min(n, i + 2 * k) + 1] --;
        }
    }

    cout << (ans ? ans : -1) << '\n';//输出答案

    return 0;
}

LeetCode 2528.最大化城市的最小电量

long long pre[100007], add[100007];

class Solution {
public:
    long long maxPower(vector<int>& stations, int r, int k) {
        int n = stations.size();
        // 重置前缀和数组
        memset(pre, 0, sizeof(long long) * n);
        for (int i = 0; i < n; ++ i) {
            // 相当于维护一个左闭右开区间[le, ri)
            int le = max(0, i - r), ri = min(i + r + 1, n);
            // 差分数组的思路，为左端点加上 stations[i]，为右端点减去 stations[i]
            pre[le] += stations[i], pre[ri] -= stations[i];
        }
        for (int i = 1; i < n; ++ i) {
            pre[i] += pre[i - 1];// 对差分过的数组求前缀和，即可维护出初始状态下每个城市的电量
        }
        long long left = 0LL, right = 1e11, middle;
        auto check = [&]() -> bool {
            // add[i]代表新建电站以后，城市(i - 1)比初始电量多增加的电量
            memset(add + 1, 0, sizeof(long long) * n);// 从下标 1 开始，是为了方便维护前缀和
            int remain = k;// 维护剩余可建供电站数量
            for (int i = 1; i <= n; ++ i) {
                add[i] += add[i - 1];
                long long need = max(0LL, middle - add[i] - pre[i - 1]);// 维护出让城市(i - 1)的电量达到middle及以上至少所需电量
                if (need > remain) return false;// 数量不足，判断为不可能满足，返回false
                remain -= need;// 否则就是可以满足
                // 用差分的思路继续维护数组add
                add[i] += need;
                add[min(i + r + r + 1, n + 1)] -= need; 
            }
            return true;
        };
        // 二分法维护出最大答案
        while (left < right) {
            middle = left + right + 1 >> 1;
            if (check()) left = middle;
            else right = middle - 1;
        }
        return left;
    }
};