【莫队算法】洛谷 P1494 [国家集训队] 小 Z 的袜子

前言

简介

莫队算法是一种用于高效处理离线区间查询问题的算法，由莫涛在2009年提出。它通过对查询进行特殊排序来优化时间复杂度。莫队算法的核心思想是：利用前一个查询结果，通过左右指针快速移动来计算出下一个查询的结果。

想要学习莫队，可以参考罗勇军（b站账号：三金蝈蝈）的视频讲解：https://www.bilibili.com/video/BV1sX4y1z7ed/?spm_id_from=333.337.search-card.all.click&vd_source=a7061d90bb9470aa775ae3cdb7d30738
另外本文的一些图片借鉴了罗老师视频的一些图片，若有侵权，可以联系删除。

使用条件

• 离线查询：所有查询已知，且可以重新排序
• 区间查询：查询关于区间 [l, r] 的信息
• 可增量性：已知查询 [l, r] 的结果，可以快速计算 [l - 1, r], [l + 1, r], [l, r - 1] 或 [l, r + 1] 的结果

适用场景

1. 区间不同数字个数
2. 区间众数
3. 区间逆序对计数

题目

https://www.luogu.com.cn/problem/P1494

题解

哈密顿路径：曼哈顿路径是指在一张图中，能够恰好访问图中每个顶点一次且仅一次的路径。

曼哈顿距离：是一个几何和度量概念，曼哈顿距离定义了在具有固定方格的坐标系（如城市网格、棋盘格）中两点之间的最短路径长度。公式为：对于两点 \((x_1, y_1)\) 和 \((x_2, y_2)\)，距离 \(d = |x_1 - x_2| + |y_1 - y_2|\)。

哈密顿路径的“好坏”的判断标准，在于这条路径的代价大小。而曼哈顿距离具备一个重要特性：曼哈顿距离本身就是一个路径长度，具备可加性。因此，曼哈顿距离可以成为哈密顿路径“好坏”的一个判断标准。

对于本题，考虑从 \((x_i, y_i)\) 移动到 \((x_j, y_j)\)，代价便是这两点之间的曼哈顿距离。对于 \(m\) 次询问，曼哈顿距离之和便是哈密顿路径。那么明显越短的哈密顿路径，会是更优解，由于边的数量不会减少，因此只能考虑尽量缩短曼哈顿距离之和。

首先考虑暴力法：把查询的区间先按左端点进行排序，若左端点相同则按右端点排序（当然也可以先右再左）。不妨用以下数据作为测试用例：

5 2
1 2 2 1 4
2 9
3 5

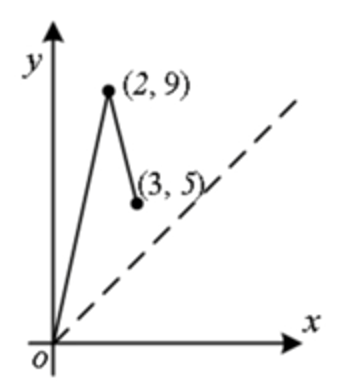
若走的路径为 \((0, 0) -> (2, 9) -> (3, 5)\)，哈密顿路径长度为：$$Len_1 = |2 - 0| + |9 - 0| + |2 - 3| + |9 - 5| = 16;$$
若走的路径为 \((0, 0) -> (3, 5) -> (2, 9)\)，哈密顿路径长度为：$$Len_2 = |3 - 0| + |5 - 0| + |2 - 3| + |9 - 5| = 13.$$

上述测试用例，可以简单说明暴力法不一定可以做到哈密顿尽可能小。

莫队算法的排序：把数组分块，然后把查询的区间按左端点所在块的序号排序，如果左端点的块相同，再按右端点排序（同样也可以先右再左，经测试，本题先右再左运行时间会略优秀一点）。

莫队算法的几何解释：

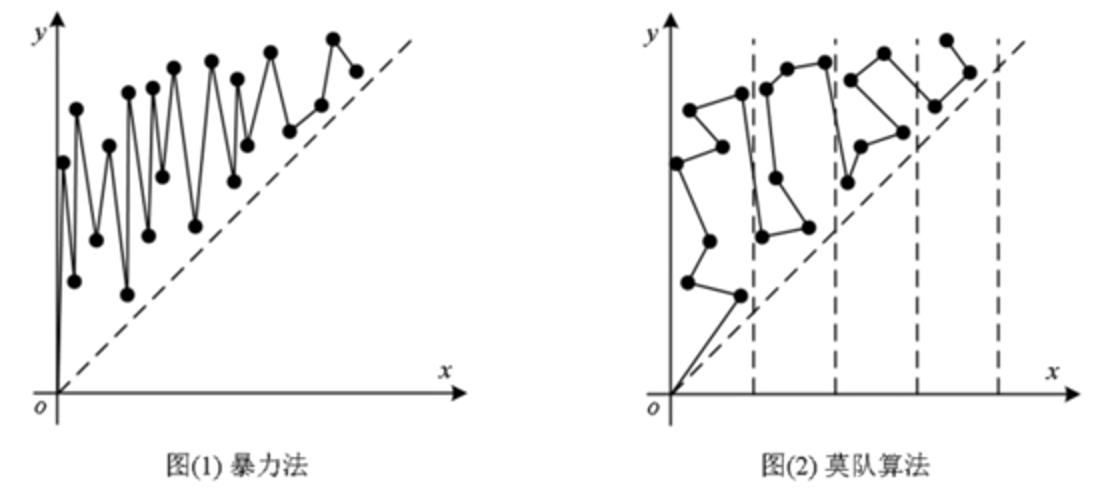
• 图（1）是暴力法排序后的路径，所有的点按 \(x\) 坐标排序，路径沿 \(y\) 轴方向来回往复，震荡幅度可能非常大，以致于哈密顿路径较“坏”。
• 图（2）是莫队算法排序后的路径，它将 \(x\) 轴分块，每个块内的点按 \(y\) 坐标进行排序，在区间内沿 \(x\) 轴方向来回往复，此时震荡的幅度被控制在块内，形成一条较“好”的哈密顿路径。
  

从 \(n\) 只袜子中挑选出 \(2\) 只袜子，组合数为 \(C^{2}_{n} = \frac{n \times (n-1)}{2}\)。想要选出的袜子颜色相同，只能从相同颜色的袜子选 \(2\) 只。假设每种颜色的袜子分别有 \(x_1, x_2, ..., x_m\) 只，若 \(x_i \leq 1\)，明显不存在合法方案，直接跳过；否则可以有 \(C_{x_i}^{2}\) 种方案。因此，从 \(n\) 只袜子中挑选出 \(2\) 只颜色相同的袜子的概率为：$$p = \frac{\frac{x_1 \times (x_1 - 1)}{2} + ... + \frac{x_i \times (x_i - 1)}{2}}{\frac{n \times (n - 1)}{2}} = \frac{x_1 \times (x_1 - 1) + ... + x_i \times (x_i - 1)}{n \times (n - 1)}，其中 x_i \geq 2.$$

参考代码

#include<bits/stdc++.h>
#include<ranges>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
using namespace std;
typedef long long ll;

/*分块*/
template <typename T>
class Piece {
private:
    static const int L = 710;//块数上限
    int len;//块长
public:
    static const int N = 5e5 + 7;//元素个数
    int n;
    T a[N];
    int lidx[L];//第 i 块的左下标
    int ridx[L];//第 i 块的右下标

    Piece(int n) {
        len = sqrt(n);
        for (int i = 0; i < n; ++ i) cin >> a[i];
        for (int i = 0, j = 0; i < n; i += len, ++ j) {
            lidx[j] = i;//左闭
            ridx[j] = min(i + len, n);//右开
        }
    }

    /*获取下标 x 所在的块的索引*/
    int getPieceId(int x) {
        return x / len;
    }

    /*判断下标 x 是否为块的左边界*/
    bool isLeftBoundary(int x) {
        return x % len == 0;
    }

    /*判断下标 x 是否为块的右边界*/
    bool isRightBoundary(int x) {
        return (x + 1) % len == 0;
    }

    /*获取第 pid 块的大小，即这个块的元素个数*/
    int getPieceSize(int pid) {
        return min(n, (pid + 1) * len) - pid * len;
    }
};

/*莫队算法：解决区间问题*/
class MoAlgorithm: public Piece<int> {
private:
    const static int QN = 5e5 + 7;
    int m;//询问次数
    int cnt[N];//统计元素个数
    ll ans = 0LL;
    struct Query {
        int l, r, id;//询问的区间左右端点及询问id
        ll numerator, denominator;
    } q[QN];//莫队属于离线算法，维护询问
public:
    MoAlgorithm(int n, int m): Piece<int>(n), m(m) {
        for (int i = 0; i < m; ++ i) {
            cin >> q[i].l >> q[i].r;
            -- q[i].l, -- q[i].r;
            q[i].id = i;
        }
        /*自定义莫队算法排序规则*/
        sort(q, q + m, [&](const Query& q1, const Query& q2) {
            return getPieceId(q1.r) != getPieceId(q2.r) ? q1.r < q2.r : q1.l < q2.l;
        });
        for (int i = 0, l = 1, r = 0; i < m; ++ i) {
            while (l > q[i].l) add(a[-- l]);//左扩展
            while (r < q[i].r) add(a[++ r]);//右扩展
            while (l < q[i].l) del(a[l ++]);//左删除
            while (r > q[i].r) del(a[r --]);//右删除
            if (l == r) {//需要特判区间大小为 1 的情况，避免分母是 0
                q[i].numerator = 0, q[i].denominator = 1;
                continue;
            }
            ll diff = r - l;
            q[i].denominator = diff * (diff + 1LL);
            q[i].numerator = ans;
            int igcd = gcd(q[i].numerator, q[i].denominator);
            q[i].numerator /= igcd, q[i].denominator /= igcd;
        }
    }

    void add(int x) {
        ans += cnt[x] << 1LL;
        ++ cnt[x];
    }

    void del(int x) {
        ans -= (cnt[x] - 1) << 1LL;
        -- cnt[x];
    }

    void out() {
        sort(q, q + m, [&](Query &q1, Query &q2) {
            return q1.id < q2.id;
        });
        for (int i = 0; i < m; ++ i) cout << q[i].numerator << '/' << q[i].denominator << '\n';
    }
};

int main() {
    IOS
    int n, m;
    cin >> n >> m;
    MoAlgorithm mo(n, m);
    mo.out();
    return 0;
}