神经网络反向传播更新原理

神经网络反向传播更新原理

一、总结

一句话总结：

A、输入x---(w1和b2)-->中间输出h（省略很多层）---(wi和bi)-->输出y-->loss函数

B、现在的需求是loss取最小值，可以求出loss对所有参数的梯度，让沿梯度下降的方向更新参数，例如w1= w1-lr*∂(loss)/∂(w1)

C、这样多次更新，各个参数就一直在往loss的极小值处靠，并且某些参数的梯度为0之后，也并不影响其它参数的继续更新

 

 

1、每一个参数的反向传播更新规律？

∂(loss)/∂(w1)=(∂(loss)/∂(y))*(∂(y)/∂(h))*(∂(h)/∂(w1)) 

 

2、各层参数w(上标1)(下标12)，w(l表示层)(ij)的更新顺序是怎么样的？

同时更新，因为可以求出loss对这些所有参数的梯度，这些参数用w1= w1-lr*∂(loss)/∂(w1)的方式就可以都更新

 

 

 

二、神经网络反向传播更新原理

转自或参考：“反向传播算法”过程及公式推导（超直观好懂的Backpropagation）
https://blog.csdn.net/ft_sunshine/article/details/90221691

 

 

 

 

 

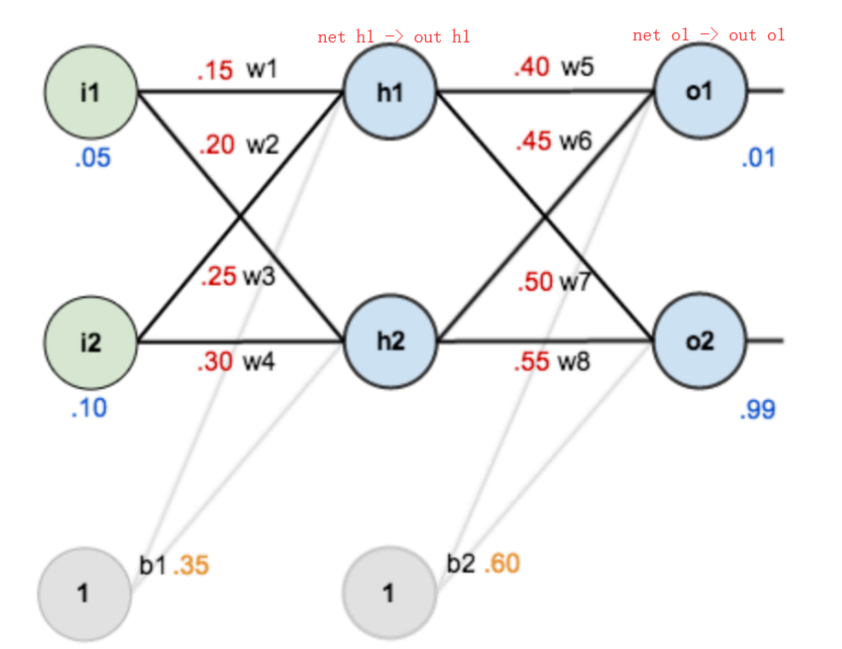
下面是反向传播（求网络误差对各个权重参数的梯度）：

我们先来求最简单的，求误差E对w5的导数。首先明确这是一个“链式求导”过程，要求误差E对w5的导数，需要先求误差E对out o1的导数，再求out o1对net o1的导数，最后再求net o1对w5的导数，经过这个链式法则，我们就可以求出误差E对w5的导数（偏导），如下图所示：

导数（梯度）已经计算出来了，下面就是反向传播与参数更新过程：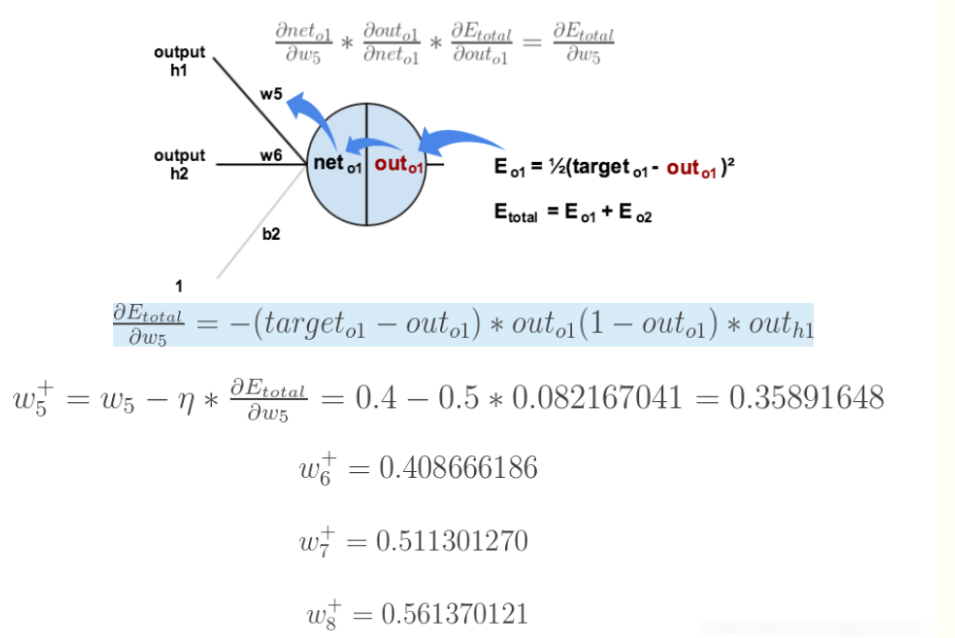

 

 

上面的图已经很显然了，耐心看一下上面的几张图，一定能看懂的。

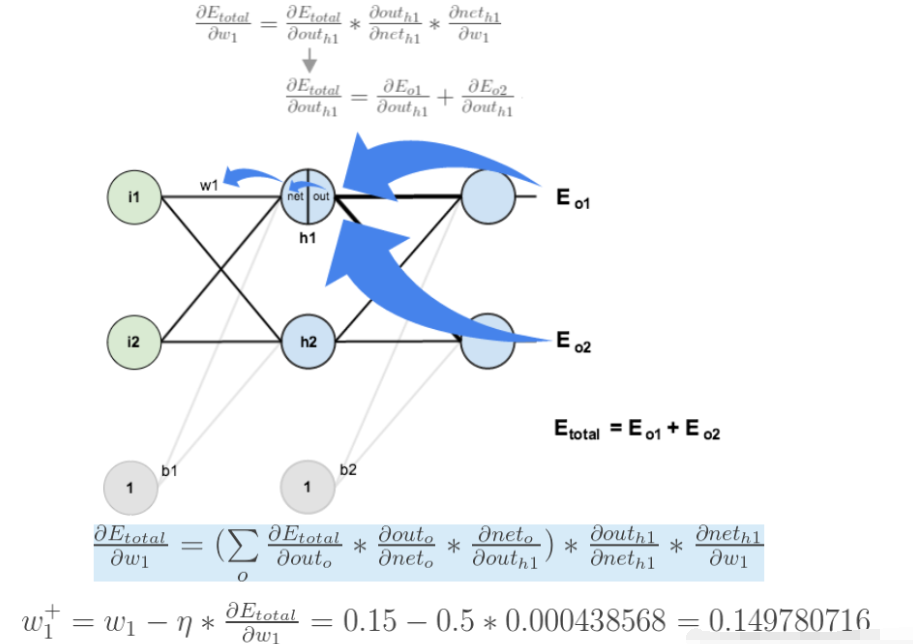
如果要想求误差E对w1的导数，误差E对w1的求导路径不止一条，这会稍微复杂一点，但换汤不换药，计算过程如下所示：