微信扫一扫打赏支持

机器学习准备---4.3、感知器原理与代码

机器学习准备---4.3、感知器原理与代码

一、总结

一句话总结：

1、W转置(k)*xi<=0，就更新权向量即可，W(k+1)=W(k)+cXi
2、只要有一个样本不满足，就重新更新权重，直到所有样本都满足
flag = True
while(flag):
    flag = False
    for i in range(len(X)):
        x = X[i,:].reshape(-1,1)
        # 小于0的话，权重增加
        if np.dot(W.T,x)<=0:
            W = W + x
            flag = True

 

 

 

二、机器学习中感知器 算法原理、方法及代码实现

转自或参考：机器学习--感知机算法原理、方法及代码实现
https://www.cnblogs.com/lsm-boke/p/12213023.html

1.感知器算法原理

两类线性可分的模式类：，设判别函数为：。

　　　　　　　　　　　　　　　　　　

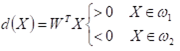
 　　　　对样本进行规范化处理，即类样本全部乘以(-1)，则有：

　　　　　　　　　　　　　　　　　　　　

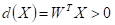
感知器算法通过对已知类别的训练样本集的学习，寻找一个满足上式的权向量。

2.算法步骤

（1）选择N个分属于和类的模式样本构成训练样本集{ X1,  …, XN }构成增广向量形式，并进行规范化处理。任取权向量初始值W(1)，开始迭代。迭代次数k=1。

（2）用全部训练样本进行一轮迭代，计算WT(k)Xi 的值，并修正权向量。分两种情况，更新权向量的值：

　　　　若   ，分类器对第 i 个模式做了错误分类，权向量校正为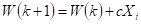：  ，c为整的校正增量。

　　　　‚若 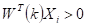  ，分类正确，权向量不变， 。

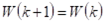　统一写成：

　　　　　　

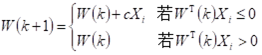
（3）分析分类结果：只要有一个错误分类，回到（2），直至对所有样本正确分类。

　　感知器算法是一种赏罚过程：

　　　　分类正确时，对权向量“赏”——这里用“不罚”，即权向量不变；

　　　　分类错误时，对权向量“罚”——对其修改，向正确的方向转换。

3.代码示例

#感知机算法
import numpy as np
import matplotlib.pyplot as plt

X0 = np.array([[1,0],
              [0,1],
              [2,0],
              [2,2]])
X1 = np.array([[-1,-1],
              [-1,0],
              [-2,-1],
              [0,-2]])

#将样本数据化为增广向量矩阵
ones = -np.ones((X0.shape[0],1))
X0 = np.hstack((ones,X0))
ones = -np.ones((X1.shape[0],1))
X1 = np.hstack((ones,X1))

#对样本进行规范化处理
X = np.vstack((-X0,X1))
plt.grid()
plt.scatter(X0[:,1],X0[:,2],c = 'r',marker='o',s=500)
plt.scatter(X1[:,1],X1[:,2],c = 'g',marker='*',s=500)
W = np.ones((X.shape[1],1))

flag = True
while(flag):
    flag = False
    for i in range(len(X)):
        x = X[i,:].reshape(-1,1)    
        if np.dot(W.T,x)<=0:
            W = W + x
            flag = True
p1=[-2.0,2.0]
p2=[(W[0]+2*W[1])/W[2],(W[0]-2*W[1])/W[2]]
plt.plot(p1,p2)
plt.show()

输出结果：

　　

 

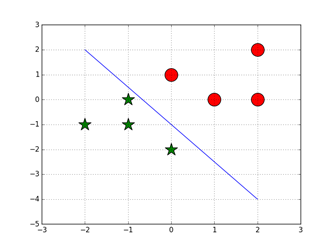
三、代码具体过程

#感知机算法
import numpy as np
import matplotlib.pyplot as plt

X0 = np.array([[1,0],
              [0,1],
              [2,0],
              [2,2]])
X1 = np.array([[-1,-1],
              [-1,0],
              [-2,-1],
              [0,-2]])
In [2]:
print(X0.shape)
print(X0.shape[0])

(4, 2)
4
In [3]:
#将样本数据化为增广向量矩阵
ones = -np.ones((X0.shape[0],1))
# 生成4行1列
print(ones)
X0 = np.hstack((ones,X0))
print(X0)

[[-1.]
 [-1.]
 [-1.]
 [-1.]]
[[-1.  1.  0.]
 [-1.  0.  1.]
 [-1.  2.  0.]
 [-1.  2.  2.]]
In [4]:
ones = -np.ones((X1.shape[0],1))
print(ones)
X1 = np.hstack((ones,X1))
print(X1)

[[-1.]
 [-1.]
 [-1.]
 [-1.]]
[[-1. -1. -1.]
 [-1. -1.  0.]
 [-1. -2. -1.]
 [-1.  0. -2.]]
In [5]:
plt.grid()
plt.scatter(X0[:,1],X0[:,2],c = 'r',marker='o',s=500)
plt.scatter(X1[:,1],X1[:,2],c = 'g',marker='*',s=500)
Out[5]:
<matplotlib.collections.PathCollection at 0x208ab449508>
In [6]:
#对样本进行规范化处理
X = np.vstack((-X0,X1))
X
Out[6]:
array([[ 1., -1., -0.],
       [ 1., -0., -1.],
       [ 1., -2., -0.],
       [ 1., -2., -2.],
       [-1., -1., -1.],
       [-1., -1.,  0.],
       [-1., -2., -1.],
       [-1.,  0., -2.]])
In [9]:
W = np.ones((X.shape[1],1))
print(W)
print(X.shape)

[[1.]
 [1.]
 [1.]]
(8, 3)
In [12]:
print(len(X)) # 总共8个样本

8
In [13]:
X[0,:]
Out[13]:
array([ 1., -1., -0.])
In [14]:
x = X[0,:].reshape(-1,1)
x
Out[14]:
array([[ 1.],
       [-1.],
       [-0.]])
In [15]:
print(W.T,x)

[[1. 1. 1.]] [[ 1.]
 [-1.]
 [-0.]]
In [16]:
print(np.dot(W.T,x))

[[0.]]
In [17]:
print(W + x)

[[2.]
 [0.]
 [1.]]
In [18]:
flag = True
while(flag):
    flag = False
    for i in range(len(X)):
        x = X[i,:].reshape(-1,1)
        # 小于0的话，权重增加
        if np.dot(W.T,x)<=0:
            W = W + x
            flag = True
In [19]:
print(W)

[[ 2.]
 [-3.]
 [-2.]]

 

W[0]+2W[1])/W[2] (2+2(-3))/(-2)=(-4)/(-2)=2

(W[0]-2W[1])/W[2] (2-2(-3))/(-2)=8/(-2)=-4

 

In [20]:
p1=[-2.0,2.0]
p2=[(W[0]+2*W[1])/W[2],(W[0]-2*W[1])/W[2]]
plt.plot(p1,p2)
Out[20]:
[<matplotlib.lines.Line2D at 0x208ab5137c8>]
In [21]:
plt.grid()
plt.scatter(X0[:,1],X0[:,2],c = 'r',marker='o',s=500)
plt.scatter(X1[:,1],X1[:,2],c = 'g',marker='*',s=500)
p1=[-2.0,2.0]
p2=[(W[0]+2*W[1])/W[2],(W[0]-2*W[1])/W[2]]
plt.plot(p1,p2)
Out[21]:
[<matplotlib.lines.Line2D at 0x208ab55e048>]

 

 

 
posted @ 2020-07-23 22:11  范仁义  阅读(380)  评论(0)    收藏  举报