二叉树

树的基本概念

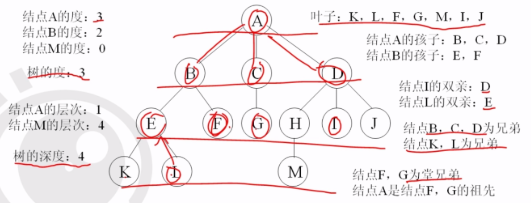
一对多，树状关系。

有且就有一个根节点，其他的节点为互不相交的有限集合，树的定义是递归的定义。

一个节点的子树的个数为该节点的度数，一棵树的度数是指该树中节点的最大度数。

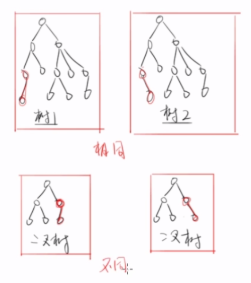
二叉树

二叉树与树的不同点

二叉树的性质

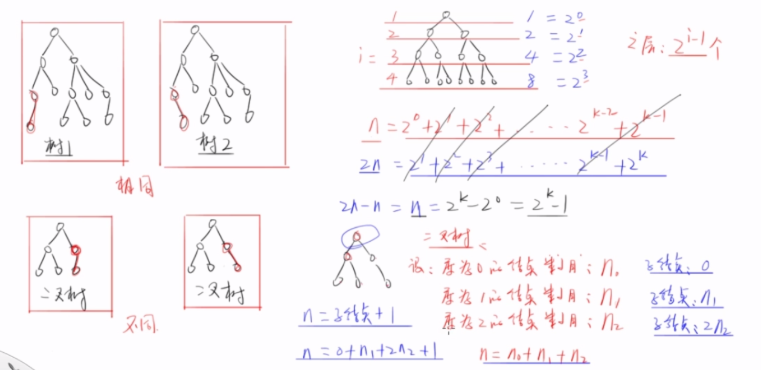
满二叉树与完全二叉树

二叉树的顺序存储结构

二叉树的链式存储结构

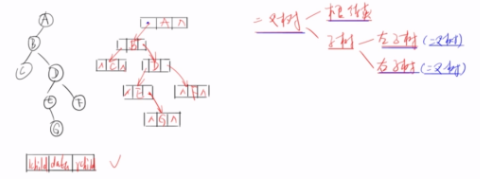
typedef char datatype_bt;
typedef struct btreenode{
    datatype_bt data;
    struct btreenode *lchild,*rchild;
}btree_node,*btree_pnode;

#if 0 //递归实现方式
btree_pnode create_btree(void)
{
    datatype_bt ch;
    btree_pnode new;
    scanf("%c",&ch);
    if('#' == ch)
    {
        return NULL;
    }
    else{
        // 创建根节点
        new = (btree_pnode)malloc(sizeof(btree_node));
        if(NULL == new)
        {
            perror("malloc");
            exit(1);
        }
        new->data = ch;
        // 用相同的方法创建左子树
        new->lchild = create_btree();
        // 用相同的方法创建右子树
        new->rchild = create_btree();
    }
}
else
void create_btree(btree_pnode *T)
{
    datatype_bt ch;
    scanf("%c",&ch);
    if('#' == ch){
        *T = NULL;
    }
    else{
        //创建根节点
        *T = (btree_pnode)malloc(sizeof(btree_node));
        if(NULL = *T){
            perror("malloc");
            exit(1);
        }
        (*T)->data = ch;
        create_btree(&(*T)->lchild);
        create_btree(&(*T)->rchild);
    }
}

二叉树的遍历

由于二叉树的递归性质，遍历算法也是递归的，三种基本遍历算法：

• 先上后下的按层次遍历
• 先左（子树）后右（子树）的遍历
• 先左（子树）后右（子树）的遍历

二叉树的先序递归遍历

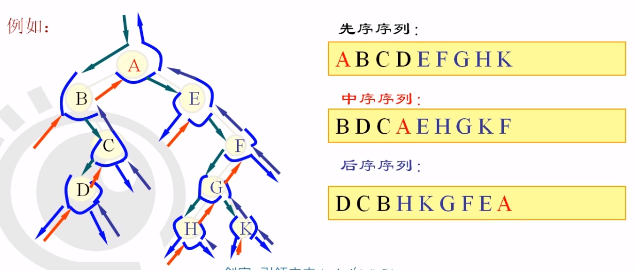
按正常情况，每个节点都会经过3次，但我们只需要遍历访问一次，这便造成不同的结果：

• 先序序列：第一次经过的时候就去访问它；
• 中序序列：第二次经过的时候去访问它；
• 后序序列：第三次经过的时候去访问它：
  

// 先序遍历
void pre_order(btree_pnode t)
{
    if(t != NULL){
        // 访问根节点
        printf("%c",t->data);
        // 先序遍历左子树
        pre_order(t->lchild);
        // 先序遍历右子树
        pre_order(t->rchild);
    }
}

二叉树的层次遍历

链式队列实现层次遍历

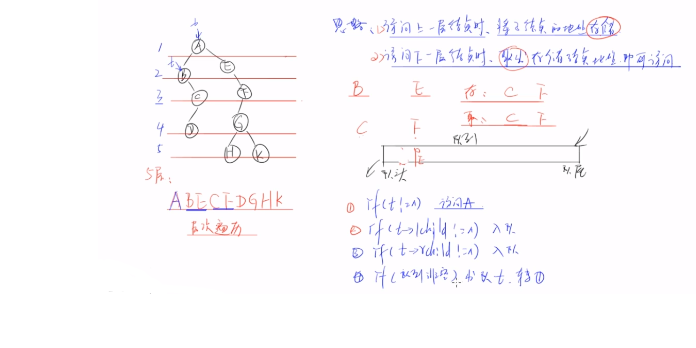
void level_order(btree_pnode t)
{
    linkqueue_pnode q;
    init_linkqueue(&q);
    while(t != NULL){
        printf("%c",t->data);
        if(t->lchild != NULL)
            in_linkqueue(t->lchild,q);
        if(t->rchild != NULL)
            in_linkqueue(t->rchild,q);
        if(!is_empty_linkqueue(q))
            out_linkqueue(q,&t);
        else
            break;
    }
}