CF1343E Weights Distributing 题解

一道思维题。

首先我们可以发现实际上我们如果能够在 $a \to b \to c$ 上的路径上将总和排的尽量小那么一定是最优的。

于是我们可以考虑求出 $a \to b$ 的最短路以及 $b \to c$ 的最短路然后其和的结果就是总的最短路，将小的丢到这些路径上面就好了

……吗？

实际上还没有，因为上述做法并没有考虑到 $a \to b$ 和 $b \to c$ 两条路径重合的情况，如图：

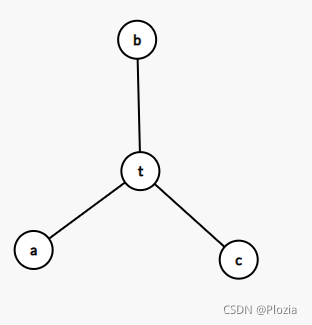
此时你会发现实际上 $b \to t$ 这条路径会被统计两次，但是按照上述做法这两次统计实际上是不同的结果。

所以实际上我们需要在 $b \to t$ 这条路径上排上最小的几个权值，然后剩下的就可以从小到大排啦~

考虑到这个 $t$ 是不定的，所以我们需要 $O(n)$ 枚举。

总复杂度 $O(Tn)$。

Code：GitHub CodeBase-of-Plozia CF1343E Weights Distributing.cpp