P4211 [LNOI2014]LCA 题解

设询问 $(l,r,z)$ 表示 $\sum_{i=1}^{r}dep[LCA(i,z)]$。

首先先对询问式做一个差分：

$$(l,r,z)=(1,r,z)-(1,l-1,z)$$

那么我们可以考虑将一个询问 $(l,r,z)$ 拆成两个询问 $(1,r,z)$ 和 $(1,l-1,z)$。

然后思考对于形如 $(1,r,z)$ 的询问怎么计算贡献。

注意到对于 $dep[LCA(x,z)]$ 我们可以这样处理：先将根节点到 $x$ 的路径上所有点点权加一，然后查询根节点到 $z$ 路径上的点权和。所有点初始为 0。

这个正确性是对的，参照下面 3 张图理解即可。

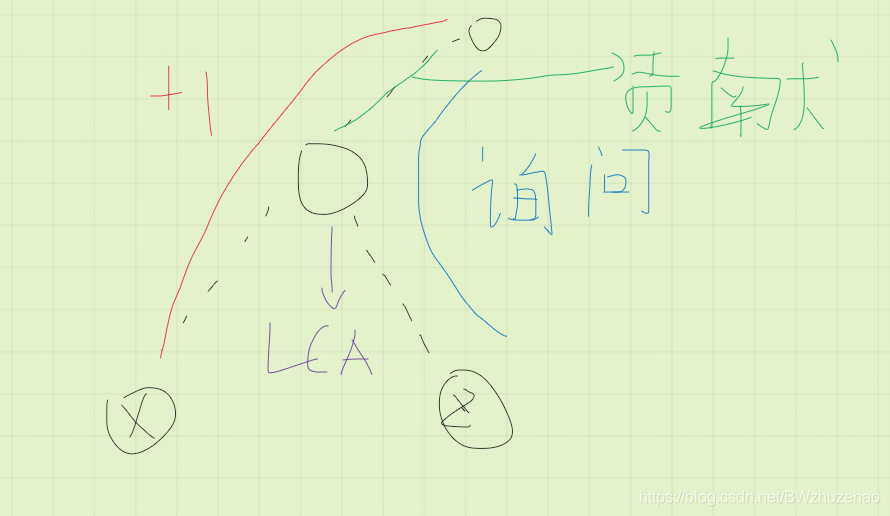
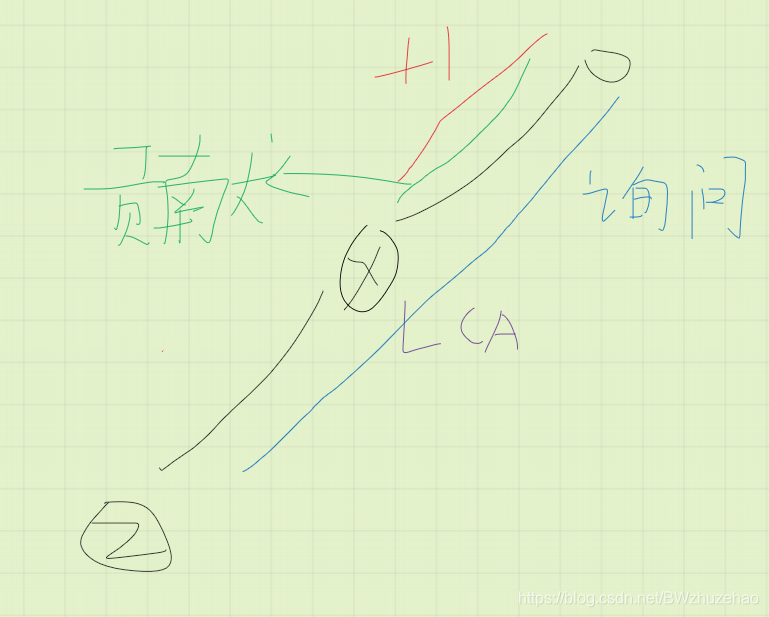
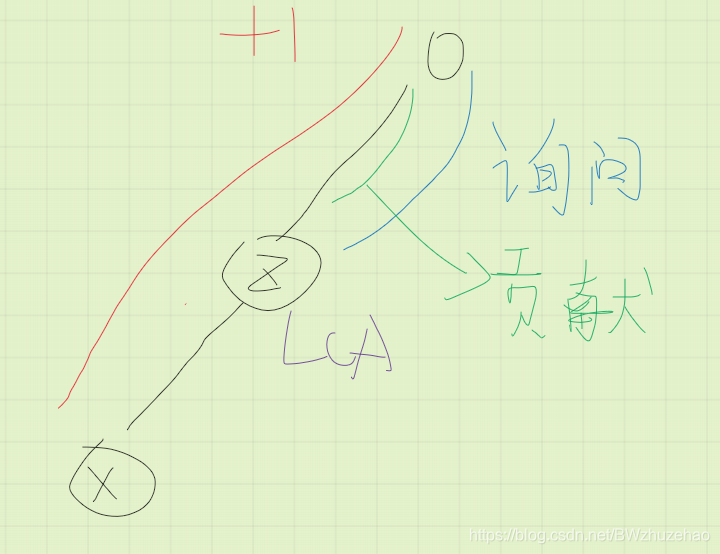
这样单次询问就解决了。

对于所有的 $(1,r,z)$ 询问，我们首先按照右端点排序，排序完成之后用一下树剖，我们就可以做到独立 $O(n \log n)$ 完成区间加操作。

路径询问？也是树剖可以完成的。

不考虑预处理复杂度，总询问复杂度是 $O(q+n \log n)$。

Code：GitHub CodeBase-of-Plozia P4211 [LNOI2014]LCA.cpp