CF1294F Three Paths on a Tree 题解

这是一道思维题。

本文约定：\(u \to v\) 表示从 \(u\) 到 \(v\) 的路径。

---

首先简化一下题意：给出一棵树，求出三个点使得三个点之间两两路径并的长度最大。

显然我们不能枚举这三个点，复杂度 \(O(n^3)\) 过大，不能接受。

做这道题需要一个重要结论：树的直径的两个端点一定是要被选中的。

简单证明：

假设树的直径的两个端点是 \(u_1,v_1\)，选的是 \(u,v,w\) 三个点，\(u \to v\) 并不是树的直径。

设 \(u \to v\) 和 \(u \to w\) 交于 \(P\) 点，如果 \(u_1 \to v_1\) 也经过 \(P\) 点，那么显然将 \(u,v,w\) 中的其中两个点换成直径一定更优。

如果 \(u_1 \to v_1\) 不经过 \(P\) 点，那么就会出现如下图几种情况：

1. 树的直径在 \(P\) 的第四棵子树上：

情况 1：

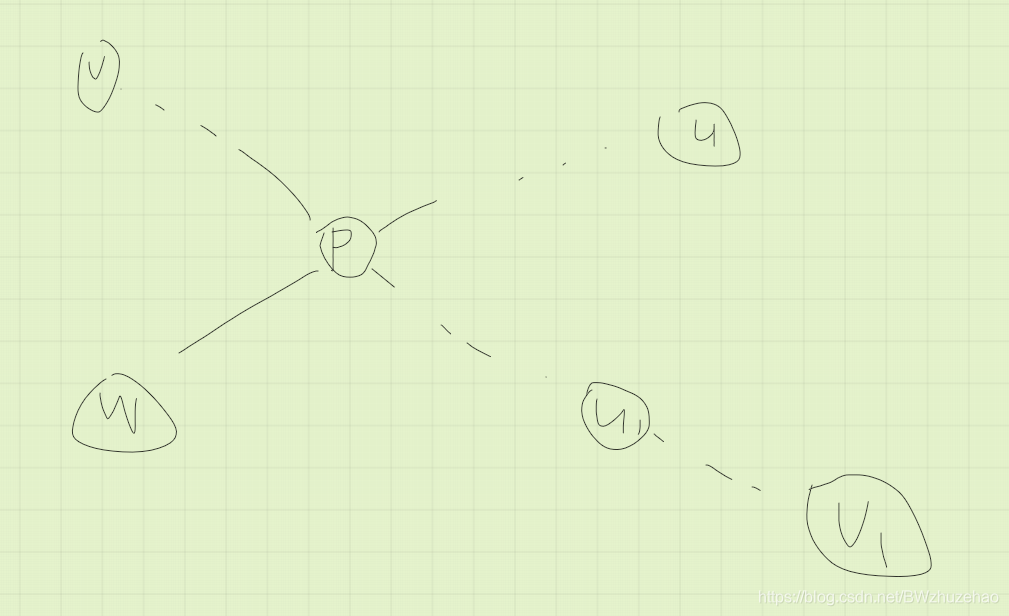
但显然这个时候 \(u_1 \to v_1\) 根本就不是直径。

情况 2：

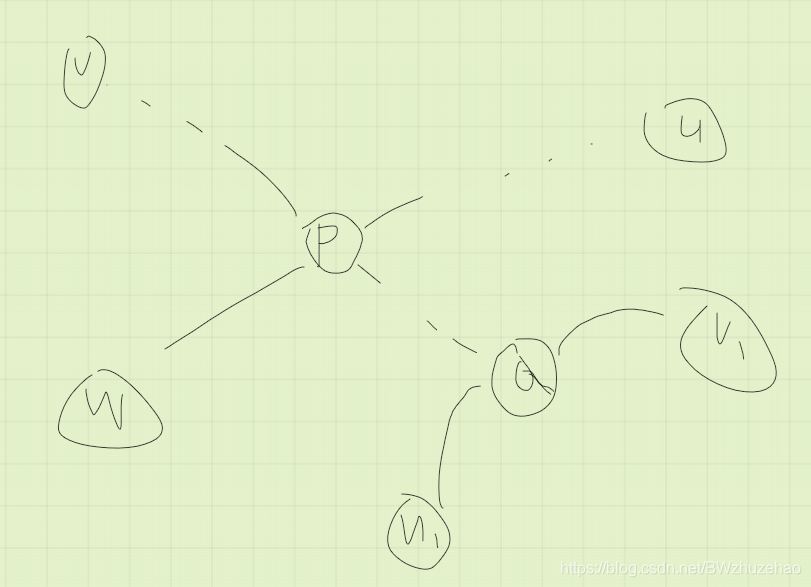
对于这一种情况，大可以把 \(u,v,w\) 中的其中一个点换成 \(u_1,v_1\)，因为这么做一定能够增加路径长度。

既然换了一个点能够增加路径长度，假设现在的点是 \(u_1,v,w\)，那么如果把 \(v\) 换成 \(v_1\) 也能够增加路径长度（否则就不是树的直径了）

综上，原命题成立。

---

在证明了这个结论之后，那么 \(u \to v\) 就一定是直径了。

怎么确定 \(w\) 呢？看图：

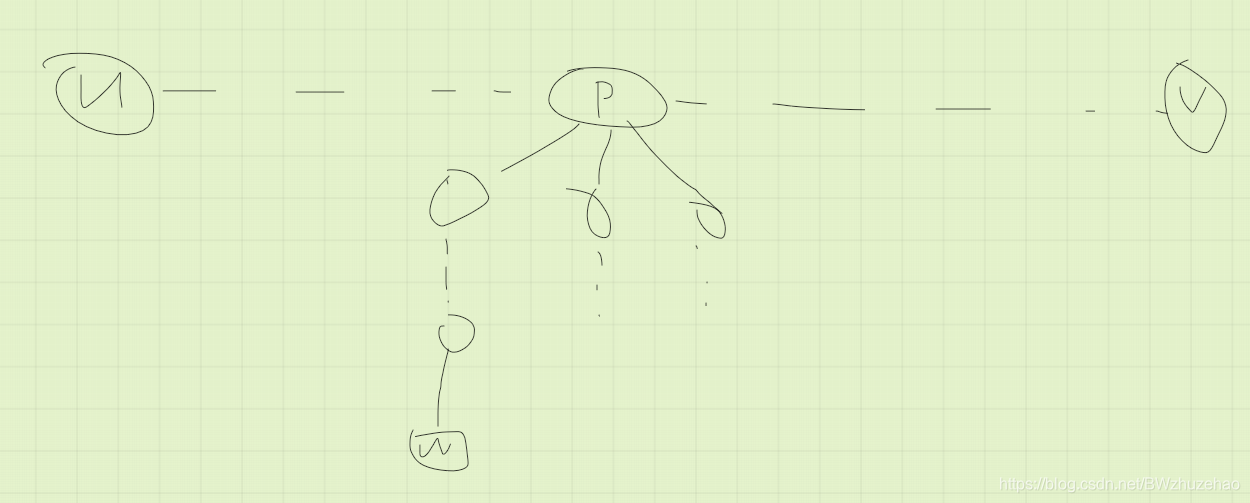
对于 \(u \to v\) 上的每一个点 \(P\) 而言（除去 \(u,v\)），我们将其旁边的几棵子树拎出来，直接在这几棵子树上面找出离 \(P\) 最远的点就可以了。

---

代码里面需要注意的细节：

• 小心链的数据，细节处理不当一条链就会把你卡成 \(w=v\) 或者 \(w=u\)。

Code：GitHub CodeBase-of-Plozia CF1294F Three Paths on a Tree.cpp