DP专题-盲点扫荡：树形 DP

目录

1. 前言

本篇文章是作者写的第 3 篇树形 DP 博文，对树形 DP 这一算法做一个复习与总结，同时进行盲点扫荡。

2. 题单

题单：

普通树形 DP

P4395 [BOI2003]Gem 气垫车

首先一种显然的想法是直接 1/2 染色。

但是很遗憾这个做法是错的，可以构造出如下反例：

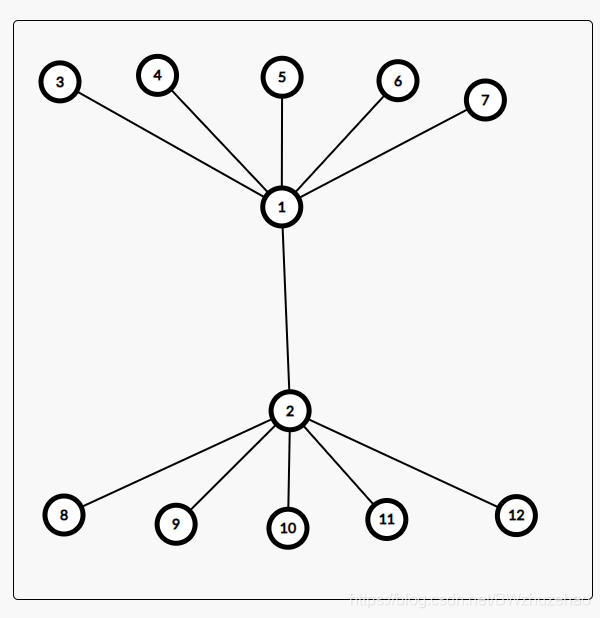
在这里插入图片描述

显然 1,2 这两个节点应该一个填 2 一个填 3，但如果只是 1/2 染色就会得到错误答案。

因此考虑树形 DP。

设 \(f_{i,j}\) 表示在第 \(i\) 个点填 \(j\) 数字的时候的最小花费。

那么就有转移方程：

\[f_{u,j}=j+\sum_{u \to v}\min\{f_{v,k} | k \ne j\} \]

这个方程还是比较好理解的吧qwq

到这里会出现两条路：

  1. 如果写法是数字与点数同阶，那么复杂度是 \(O(n^3)\) 的。为了降下复杂度，可以只存最大值与次大值及其填的数，这样可以优化转移。
  2. 当然也可以手动调整一下最大的数字上限，题解区有人说过最大数为 \(\log n\)，但是我不会证qwq，我采用的是这种方法。

My Code：

/*
========= Plozia =========
    Author:Plozia
    Problem:P4395 [BOI2003]Gem 气垫车
    Date:2021/5/26
========= Plozia =========
*/

#include <bits/stdc++.h>

typedef long long LL;
const int MAXN = 10000 + 10;
const LL INF = 0x7f7f7f7f7f7f7f7f;
int n, Head[MAXN], cnt_Edge = 1;
LL f[MAXN][70];
struct node { int to, Next; } Edge[MAXN << 1];

int Read()
{
    int sum = 0, fh = 1; char ch = getchar();
    for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
    for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
    return sum * fh;
}
LL Max(LL fir, LL sec) { return (fir > sec) ? fir : sec; }
LL Min(LL fir, LL sec) { return (fir < sec) ? fir : sec; }
void add_Edge(int x, int y) { ++cnt_Edge; Edge[cnt_Edge] = (node){y, Head[x]}; Head[x] = cnt_Edge; }

void DP(int now, int father)
{
    for (int i = 1; i <= 50; ++i) f[now][i] = i;
    bool flag = 0;
    for (int i = Head[now]; i; i = Edge[i].Next)
    {
        int u = Edge[i].to;
        if (u == father) continue ;
        DP(u, now); flag = 1;
    }
    if (flag) for (int i = 1; i <= 50; ++i) f[now][i] = i;
    for (int i = Head[now]; i; i = Edge[i].Next)
    {
        int u = Edge[i].to;
        if (u == father) continue ;
        for (int j = 1; j <= 50; ++j)
        {
            LL sum = INF;
            for (int k = 1; k <= 50; ++k)
                if (j != k) sum = Min(sum, f[u][k]);
            f[now][j] += sum;
        }
    }
}

int main()
{
    n = Read();
    for (int i = 1; i < n; ++i)
    {
        int x = Read(), y = Read();
        add_Edge(x, y); add_Edge(y, x);
    }
    DP(1, -1); LL ans = INF;
    for (int i = 1; i <= 50; ++i) ans = Min(ans, f[1][i]);
    printf("%lld\n", ans); return 0;
}

P3698 [CQOI2017]小Q的棋盘

文中的 \(n,v\) 与题中的 \(n,v\) 意义刚好相反。

这道题有两种方法：普通树形 DP 和贪心。

树形 DP 的做法参见题解区，其复杂度为 \(O(nv)\)，这里只讲复杂度更低的 \(O(n)\) 做法。

首先考虑求一下从 0 开始的最长链长度，记为 \(l\)。

如果 \(l>v\)，这说明不能用 \(v\) 步走完这条最长链，那么答案就是 \(v+1\)，因为不可能有更优的走法使得经过点数大于 \(v+1\)。

如果 \(l \leq v\)，这说明能用 \(v\) 步走完这条最长链，剩余步数 \(v-(l-1)=v-l+1\)。

那么剩下的步数怎么办呢？

有一个关键点：在走完最长链之后，每多走一个点至少需要耗费两步，过去一步，回来一步。

因此我们可以将剩下的 \(v-l+1\) 拿去走这些点，可以走 \(\left\lfloor\dfrac{v-l+1}{2}\right\rfloor\) 个点。

因此此处答案就是 \(l+\left\lfloor\dfrac{v-l+1}{2}\right\rfloor\)。

有的人会问了：如果你走到了最长链底端，那么不是回去需要耗费更多的步数吗？

实际上你可以将多走点的过程看作是在走最长链的过程中出去走点，这样就是刚好一个点两步。

需要注意总共点数只有 \(n\)，因此这种情况还要与 \(n\) 取最小值。

那么为什么这个算法就是正确的呢？

首先前面已经说过，除走的链上所有点外，每额外走一个点至少需要 2 步，而链上只需要 1 步。

所以我们需要使链上的点数尽量大，所以就求最长链。

另一方面，为使点数尽量大，我们需要刚好两步一个点，而该方案的可行性上面已经解释过。

综上，该算法能够使点数最大，算法正确。

注意一点：求的不是直径，而是以 0 为起点的最长链。

My Code：

/*
========= Plozia =========
    Author:Plozia
    Problem:P3698 [CQOI2017]小Q的棋盘
    Date:2021/5/25
========= Plozia =========
*/

#include <bits/stdc++.h>

typedef long long LL;
const int MAXN = 100 + 10;
int n, v, f1[MAXN], f2[MAXN], Head[MAXN], cnt_Edge = 1, ans;
struct node { int to, val, Next; } Edge[MAXN << 1];

int Read()
{
    int sum = 0, fh = 1; char ch = getchar();
    for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
    for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
    return sum * fh;
}
int Max(int fir, int sec) { return (fir > sec) ? fir : sec; }
int Min(int fir, int sec) { return (fir < sec) ? fir : sec; }
void add_Edge(int x, int y, int z) { ++cnt_Edge; Edge[cnt_Edge] = (node){y, z, Head[x]}; Head[x] = cnt_Edge; }

void dfs(int now, int father, int dis)
{
    if (dis > ans) ans = dis;
    for (int i = Head[now]; i; i = Edge[i].Next)
    {
        int u = Edge[i].to;
        if (u == father) continue ;
        dfs(u, now, dis + 1);
    }
}

int main()
{
    n = Read(), v = Read();
    for (int i = 1; i < n; ++i)
    {
        int x = Read(), y = Read();
        add_Edge(x, y, 1); add_Edge(y, x, 1);
    }
    dfs(0, -1, 1);
    if (ans > v) printf("%d\n", v + 1);
    else printf("%d\n", Min(n, (v + ans + 1) / 2));
    return 0;
}

背包类树形 DP

简要说一下背包类树形 DP 的一般套路：

设 \(f_{i,j}\) 表示以 \(i\) 为根的子树中选取 \(j\) 个符合题目要求的节点的答案，转移的时候一般利用刷表法转移，枚举 \(j,k\) 表示前面已经处理过的子树中选 \(j\) 个，当前子树中选 \(k\) 个，对 \(f_{i,j+k}\) 刷表转移。

需要注意的是转移之前要临时存一下 \(f_{i,j+k}\)，避免干扰。

当然你也可以采用改变循环顺序来避免这些问题，但是存一下可以减少思维量与出错率（万一循环顺序错了呢？）。

这里有必要提一下笔者的写代码习惯：

  1. 采用刷表法，这会让你减少大量的思维量，而且方程容易推对，不易出错。
  2. 转移的时候采用一个 \(g\) 数组临时存下 \(f_{i,j+k}\)，因为这样就无需考虑循环顺序，在 OI 中可以防止因循环顺序出错而导致的失分。

P3177 [HAOI2015]树上染色

设 \(f_{i,j}\) 表示在第 \(i\) 棵子树中，选取 \(k\) 个点染成黑色点时可以得到的最大收益。

首先我们需要注意到一个性质：对于一组黑色点对 \((u,v)\)，设其经过边 \(e\)，那么其对答案的贡献为 \(e.val\)。

那么因此假设在 \(e\) 的一边有 \(l\) 个黑色点，另一边就有 \(k-l\) 个黑色点，于是这些黑色点对对答案的贡献为 \(e.val \times l \times (k-l)\)。

根据上述性质，我们可以将距离和计算转变为对一条边两边的点数的计算。

于是对于 \(u\)，我们有转移方程（采用刷表法）：

\[f_{u,j+l}=\max\{g_j+f_{v,l}+ t \times val|u \to v\} \]

其中 \(g\) 是在转移之前临时保存的 \(f\) 以防止因为循环顺序出现转移错误，\(t=l \times (k-l)+(Size_v-l) \times (n-Size_v-(k-l))\)，也就是两边的黑色点对与白色点对的数量，\(Size_v\) 表示以 \(v\) 为根节点的子树大小。

初值为对任意节点 \(v\)，\(f_{v,0}=f_{v,1}=0\)。

对于枚举 \(j,l\)：

需要注意的是 \(j \leq Size_u,l \leq Size_v,j + l \leq k\)。

其中 \(Size_u\) 在转移时的定义并不是子树大小，而是已经其子树中已经遍历过的节点总数（包括自身）。

如果看不懂的话，看看代码就好了。

为什么不能 \(j \leq k,l \leq k, j + l \leq k\) 呢？

因为这样的复杂度是假的，为 \(O(n^2k)\)，其瓶颈在于没有限定背包容量。

而按照上述这样限定 \(j,k\) 的范围就可以做到 \(O(n^2)\)。

复杂度证明如下：

考虑任意一组同色点对 \((u,v)\)。

实际上对于这一组同色点对 \((u,v)\)，其对答案的贡献只可能在其最近公共祖先（LCA）处贡献一次，而任意两个点的 LCA 是唯一的。

因此考虑从计算点对贡献的角度计算复杂度，由于每一组同色点对只会被计算一次，而这样的点对至多只有 \(n^2\) 组，于是复杂度为 \(O(n^2)\)，证毕。

注意开 long long，尤其是 max 函数。

My Code：

/*
========= Plozia =========
    Author:Plozia
    Problem:P3177 [HAOI2015]树上染色
    Date:2021/5/26
========= Plozia =========
*/

#include <bits/stdc++.h>

typedef long long LL;
const int MAXN = 2000 + 10;
int n, k, Head[MAXN], cnt_Edge = 1, Size[MAXN];
LL f[MAXN][MAXN], g[MAXN];
struct node { int to; LL val; int Next; } Edge[MAXN << 1];

int Read()
{
    int sum = 0, fh = 1; char ch = getchar();
    for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
    for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
    return sum * fh;
}
LL Max(LL fir, LL sec) { return (fir > sec) ? fir : sec; }
LL Min(LL fir, LL sec) { return (fir < sec) ? fir : sec; }
void add_Edge(int x, int y, LL z) { ++cnt_Edge; Edge[cnt_Edge] = (node){y, z, Head[x]}; Head[x] = cnt_Edge; }

void DP(int now, int father)
{
    Size[now] = 1; f[now][0] = f[now][1] = 0;
    for (int i = Head[now]; i; i = Edge[i].Next)
    {
        int u = Edge[i].to;
        if (u == father) continue ;
        DP(u, now);
        for (int j = 0; j <= k; ++j) g[j] = f[now][j];
        for (int j = 0; j <= Size[now] && j <= k; ++j)
            for (int l = 0; l <= Size[u] && j + l <= k; ++l)
                f[now][j + l] = Max(f[now][j + l], g[j] + f[u][l] + (1ll * l * (k - l) + 1ll * (Size[u] - l) * (n - Size[u] - k + l)) * Edge[i].val);
        Size[now] += Size[u];
    }
}

int main()
{
    n = Read(), k = Read(); memset(f, -0x3f, sizeof(f));
    if (n - k < k) k = n - k;
    for (int i = 1; i < n; ++i)
    {
        int x = Read(), y = Read(), z = Read();
        add_Edge(x, y, z); add_Edge(y, x, z);
    }
    DP(1, -1); printf("%lld\n", f[1][k]); return 0;
}

P1273 有线电视网

设 \(f_{i,j}\) 表示在第 \(i\) 棵子树当中选取 \(j\) 个用户时的最大收益，那么我们的答案就是所有 \(f_{1,i}>0\) 中最大的 \(i\)。

考虑如下转移方程：

设当前枚举边为 \(u \to v\)，则有：

\[f_{u,j+k}=\max(f_{u,j+k},g_{j}+f_{v,k}-val) \]

其中 \(val\) 是这条边的边权。

初值为对于所有叶子节点 \(v\)，\(f_{v,1}=a_v\)。

My Code：

/*
========= Plozia =========
    Author:Plozia
    Problem:P1273 有线电视网
    Date:2021/5/25
========= Plozia =========
*/

#include <bits/stdc++.h>

typedef long long LL;
const int MAXN = 3000 + 10;
int n, m, a[MAXN], Head[MAXN], cnt_Edge = 1, f[MAXN][MAXN], g[MAXN][MAXN], Size[MAXN];
struct node { int to, val, Next; } Edge[MAXN << 1];

int read()
{
    int sum = 0, fh = 1; char ch = getchar();
    for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
    for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
    return sum * fh;
}
int Max(int fir, int sec) { return (fir > sec) ? fir : sec; }
int Min(int fir, int sec) { return (fir < sec) ? fir : sec; }
void add_Edge(int x, int y, int z) { ++cnt_Edge; Edge[cnt_Edge] = (node){y, z, Head[x]}; Head[x] = cnt_Edge; }

void dfs(int now, int father)
{
    f[now][0] = 0; Size[now] = 1;
    if (now >= n - m + 1 && now <= n) { f[now][1] = a[now]; return ; }
    for (int i = Head[now]; i; i = Edge[i].Next)
    {
        int u = Edge[i].to;
        if (u == father) continue ;
        dfs(u, now);
        for (int j = 0; j <= m - 1; ++j) g[now][j] = f[now][j];
        for (int j = 0; j <= Size[u]; ++j)
            for (int k = 0; k <= Size[now]; ++k)
                f[now][j + k] = Max(f[now][j + k], f[u][j] - Edge[i].val + g[now][k]);
        Size[now] += Size[u];
    }
}

int main()
{
    n = read(), m = read();
    for (int i = 1; i <= n - m; ++i)
    {
        int k = read();
        while (k--)
        {
            int y = read(), z = read();
            add_Edge(i, y, z); add_Edge(y, i, z);
        }
    }
    for (int i = n - m + 1; i <= n; ++i) a[i] = read();
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m - 1; ++j)
            f[i][j] = -0x3f3f3f3f;
    dfs(1, 1);
    for (int i = m - 1; i >= 0; --i)
        if (f[1][i] >= 0) { printf("%d\n", i); return 0; }
    printf("0\n"); return 0;
}

换根 DP

换根 DP 的一般题型是对于所有 \(i\) 作为根节点，需要求出一类问题的答案。

其一般套路如下：

首先指定一个点为根节点，做一遍只考虑子树内的树形 DP。

然后从这个点重新 DFS 遍历整棵树，自顶向下考虑父节点对这个节点的答案的影响，重新计算一遍以得到正确的答案，这个过程中通常会用到一点容斥的思想。

P3047 [USACO12FEB]Nearby Cows G

考虑换根 DP。

第一遍树形 DP：

设 \(f_{i,j}\) 表示距离第 \(i\) 个节点为 \(j\) 的所有节点的权值和。

那么对于 \(u\) 节点，有一个简单的转移方程：

\[f_{i,j}=\sum_{u \to v}f_{v,j-1} \]

初值为对于所有叶子节点 \(v\)，\(f_{v,0}=a_v\)。

第二遍 DFS：

我们已经得到了 \(f_{i,j}\)，则对于根节点而言其答案就是 \(f_{i,k}\)。

考虑非根节点的父亲 \(u\) 对儿子 \(v\) 的影响：

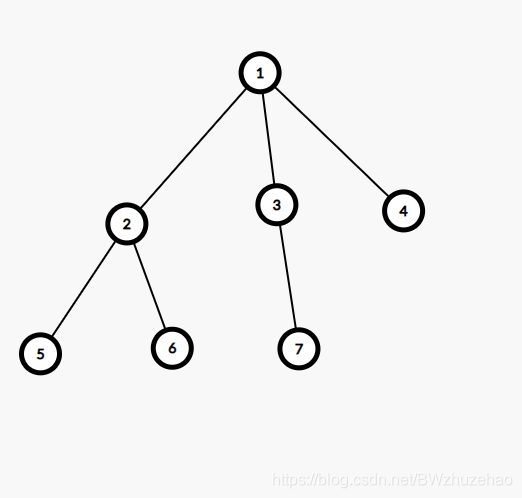
在这里插入图片描述

假设我们当前需要处理 3 号点的 \(f_{3,j}\) 的正确答案，那么考虑父节点对 3 号点的贡献应该为 \(f_{1,j-1}\)。

但是如果这样做，其子节点 7 的答案可能会被重复计算，因此我们还需要减去 \(f_{3,j-2}\)。

这样就可以得到正确的 \(f_{3,j}\) 了。

My Code:

/*
========= Plozia =========
    Author:Plozia
    Problem:P3047 [USACO12FEB]Nearby Cows G
    Date:2021/5/25
========= Plozia =========
*/

#include <bits/stdc++.h>

typedef long long LL;
const int MAXN = 1e5 + 10;
int n, k, Head[MAXN], cnt_Edge = 1, f[MAXN][30], a[MAXN];
struct node { int to, Next; } Edge[MAXN << 1];

int read()
{
    int sum = 0, fh = 1; char ch = getchar();
    for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
    for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
    return sum * fh;
}
int Max(int fir, int sec) { return (fir > sec) ? fir : sec; }
int Min(int fir, int sec) { return (fir < sec) ? fir : sec; }
void add_Edge(int x, int y) { ++cnt_Edge; Edge[cnt_Edge] = (node){y, Head[x]}; Head[x] = cnt_Edge; }

void dfs(int now, int father)
{
    f[now][0] = a[now];
    for (int i = Head[now]; i; i = Edge[i].Next)
    {
        int u = Edge[i].to;
        if (u == father) continue ;
        dfs(u, now);
        for (int j = 1; j <= k; ++j)
            f[now][j] += f[u][j - 1];
    }
}

void Change_Root(int now, int father)
{
    for (int i = Head[now]; i; i = Edge[i].Next)
    {
        int u = Edge[i].to;
        if (u == father) continue ;
        for (int j = k; j >= 2; --j) f[u][j] -= f[u][j - 2];//注意是逆序！
        //当然如果你懒也可以开一个 g 数组临时存一下 f
        for (int j = 1; j <= k; ++j) f[u][j] += f[now][j - 1];
        Change_Root(u, now);
    }
}

int main()
{
    n = read(), k = read();
    for (int i = 1; i < n; ++i)
    {
        int x = read(), y = read();
        add_Edge(x, y); add_Edge(y, x);
    }
    for (int i = 1; i <= n; ++i) a[i] = read();
    dfs(1, 0); Change_Root(1, 0);
    for (int i = 1; i <= n; ++i)
    {
        int sum = 0;
        for (int j = 0; j <= k; ++j) sum += f[i][j];
        //注意这里要求前缀和
        printf("%d\n", sum);
    }
    return 0;
}

3. 总结

树形 DP 相对别的 DP 还是比较套路的，大体分成如下几种：

  • 普通树形 DP。
  • 背包类树形 DP。
  • 换根 DP。
posted @ 2022-04-17 16:15  Plozia  阅读(94)  评论(0)    收藏  举报