图论专题-网络流-学习笔记：网络流基础
1. 前言
网络流，属于图论的一种。
网络流看上去是一个新的东西，实际上就是新瓶装旧酒，相信讲完之后你会发现这玩意的一些基础定义什么的跟 有向图 没啥差别。
因为网络流算法有点多，于是本文在讲述基础定义之外同时提供算法导航，将后续的算法学习笔记添加入本博客中。
2. 详解
首先我们需要明白一点：网络流是个啥？
实际上，网络流就是一张有向图，只不过给图上的东西换了换名字。
比如看看下面这张图。
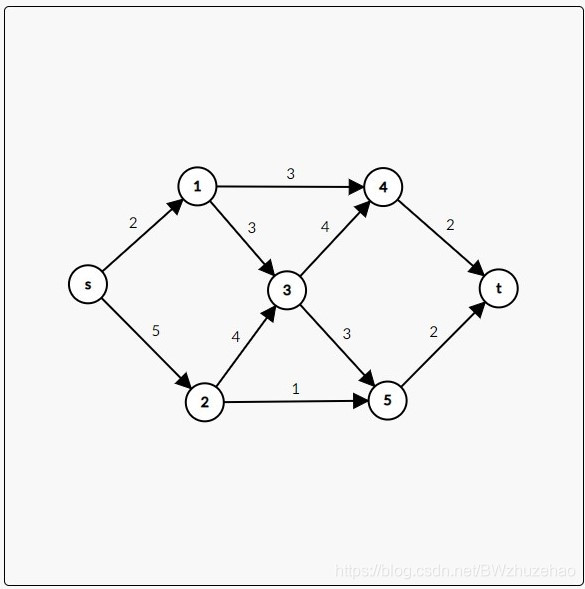
（绘图工具：Graph Editor）
看一下这张有向图，这在网络流里面叫做『网络』。
仔细看一下，你会发现图中有两个特别节点：\(s,t\)。
\(s\) 叫做『源点』，\(t\) 叫做『汇点』。
图上的边权叫做『流量』。
看不懂没关系，我初学的时候也看不懂，接下来拿一个例子来说明网络流到底是个啥：
假设 \(s\) 是一座水库，含有无穷多的水，\(t\) 是你家所在的位置，途中有 5 个湖，标号为 \(1,2,3,4,5\)，假设湖能够存下无穷多的水。
当然，水要流到你家是需要经过一些路径的，但是这些路径不是无限量送水的，比如说从 \(s\) 到 \(1\) 就只能送 \(2\) 单位的水，多的也不能送。
这样就能理解网络流了吧？
这张有向图就是网络流中的『网络』，在网络中『源点』就是水库，『汇点』就是你家，而『流量』就是每条边最多能够通过的水量。
网络流的基础定义就是这些。
3. 算法导航
导航之前先简要给出网络流中的几个算法：
- 最大流
最大流就是问从源点到汇点最多能够通过多少流量，也就是到你家最多还剩多少水。 - 最小割
最小割有一点抽象，主要就是问删掉哪些边使得源点与汇点不再连通，输出边权最小值。
可以证明，最大流=最小割。 - 最小费用最大流（简称费用流）
比如说现在运输要钱了，从一个湖到另一个湖运输是要钱的，每运一单位的水就需要一定量的钱，请问在满足最大水量的前提下最小的钱数。 - 上下界网络流
这个时候，每一条边的流量需要在一定范围 \([l,r]\) 内，不能少于 \(l\) 也不能多于 \(r\)，你需要确定每一条边的流量使得除了源点汇点之外的所有点流出量等于流入量。
或者你可以简单理解为连接湖的路径上面有些发电站，为了保证发电站正常工作，通过的水流量最少为 \(l\)，但是不能太多以免损坏机器，最多为 \(r\)。
算法学习笔记导航：
浙公网安备 33010602011771号