[物理]质点静力学 Jan. 29th

时间：2023年1月29日

---

摩擦角与全反力

四力化三力

1.木箱重为 \(mg\)，与地面间的动摩擦因数为 \(\mu\)，用斜向上的拉力 \(F\) 拉木箱使之沿水平地面匀速前进，问角 \(\alpha\) 为何值时拉力 \(F\) 最小？这个最小值为多大？

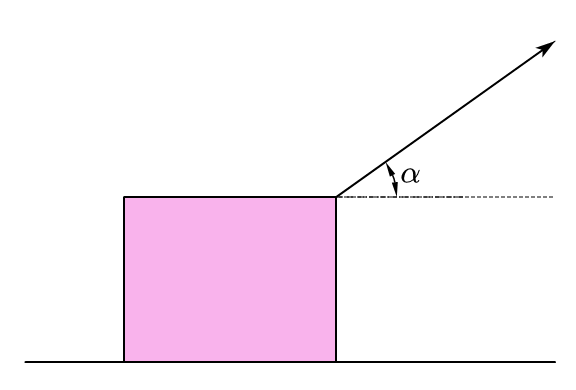
1. 沿水平方向正交分解并运用辅助角公式（大题推荐方法）

解：对木箱进行受力分析，如图

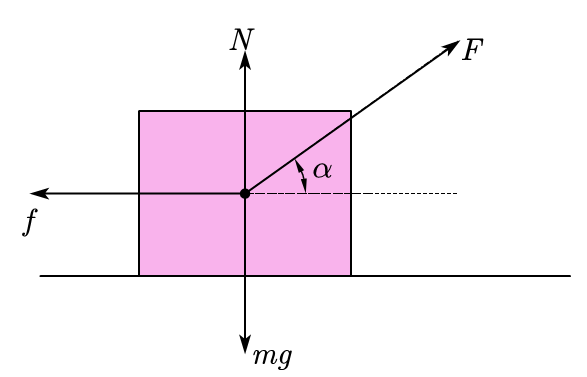
木箱受力平衡，因此

\[F\cos\alpha=\mu N\ \ \ \ \ ① \]

\[N+F\sin\alpha=mg\ \ \ \ \ ② \]

联立①②式，消去 \(N\)，得

\[F\cos\alpha=\mu (mg-F\sin\alpha)\iff F(\cos\alpha+\mu\sin\alpha)=\mu mg \]

解得

\[F=\frac{\mu mg}{\cos\alpha+\mu\sin\alpha} \]

求 \(F\) 最小值，即求 \(\cos\alpha+\mu\sin\alpha\) 最大值

\[\mu\sin\alpha+\cos\alpha=\sqrt{1+\mu^2}(\frac{\mu}{\sqrt{1+\mu^2}}\sin\alpha+\frac{1}{\sqrt{1+\mu^2}}\cos\alpha)\ \ \ \ \ ③ \]

令 \(\tan\varphi=\mu\)，则

\[③=\sqrt{1+\mu^2}(\sin\varphi\sin\alpha+\cos\varphi\cos\alpha)=\sqrt{1+\mu^2}\cos(\alpha-\varphi)\ \ \ \ \ ④ \]

当 \(\cos(\alpha-\varphi)=1\)，即 \(\alpha=\varphi\) 时，\(④\) 取最大值

此时 \(F\) 取最小值

\[F_{\min}=\frac{\mu}{\sqrt{1+\mu^2}}mg=mg\sin\varphi \]

2. 全反力（推荐小题使用）

阻碍物体运动的支持力 \(N\)（或 \(F_N\)）与摩擦力 \(f\) 的合力称为全反力，记作 \(R\) 或 \(F_R\)。

全反力的大小为 \(R=\sqrt{f^2+N^2}\)。

当 \(f\) 为滑动摩擦力时，全反力 \(R\) 与支持力 \(N\) 的夹角达到最大值。若记夹角为 \(\varphi\)，则

\[\tan\varphi=\mu \]

解：对木箱进行受力分析，记全反力为 \(R\)

由于木箱向右滑动，若记 \(R\) 与 \(N\) 间的夹角为 \(\varphi\)，则有

\[\tan\varphi=\frac{f}{N}=\frac{\mu N}{N}=\mu \]

1. 图解法（向量三角形）

木箱匀速运动，所以

\[\overrightarrow{R}+\overrightarrow{F}=-\overrightarrow{mg} \]

作出示意图，如图

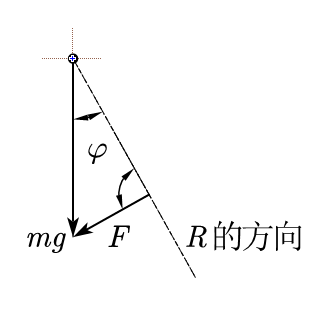
显然，当 \(F\) 与\(R\) 垂直时，\(F\) 有最小值

此时

\[F=mg\sin\varphi \]

方向与地面的夹角为 \(\varphi\)

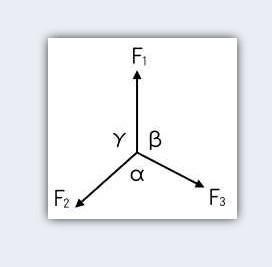
2. 拉密定理

如图，记质点受到的三个力分别为 \(F_1\)、\(F_2\)、\(F_3\)，\(F_1\) 与 \(F_2\)、\(F_2\) 与 \(F_3\)，\(F_3\) 与 \(F_1\) 间的夹角分别为 \(\gamma\)、\(\alpha\)、\(\beta\)。若质点受力平衡，则

\[\frac{F_1}{\sin\alpha}=\frac{F_2}{\sin\beta}=\frac{F_3}{\sin\gamma} \]

可以使用正弦定理和诱导公式证明。

由拉密定理，得

\[\frac{mg}{\sin(\varphi+\frac{\pi}{2}-\alpha)}=\frac{F}{\sin(\pi-\varphi)} \]

整理得

\[F=\frac{mg\sin\varphi}{\cos(\alpha-\varphi)} \]

因此，当 \(\cos(\alpha-\varphi)=1 \iff \alpha=\varphi\) 时，\(F\) 取得最小值

\[F_{\min}=mg\sin\varphi \]

---

2.一物体质量为 \(m\)，置于倾角为 \(\alpha\) 的斜面上，物体与斜面间的动摩擦因数为 \(\mu\)，若要使物体沿斜面匀速向上滑动，求拉力 \(F\) 的最小值。

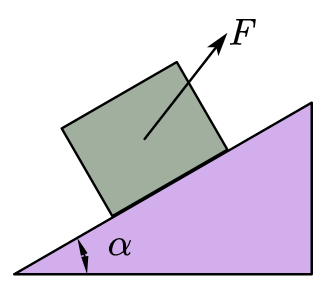
注：这里用拉密定理解决

解：设全反力 \(R\) 与支持力 \(N\) 的夹角为 \(\varphi\)，拉力 \(F\) 与斜面的夹角为 \(\theta\)

则

\[\tan\varphi=\mu \]

对物体 \(m\) 受力分析，如图

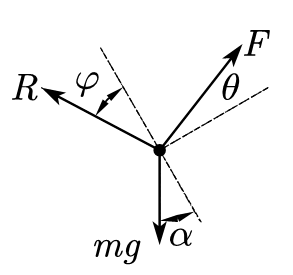
由拉密定理，得

\[\frac{mg}{\sin(\varphi+\frac{\pi}{2}-\theta)}=\frac{F}{\sin(\pi-\varphi-\alpha)} \]

整理得

\[F=\frac{mg\sin(\varphi+\alpha)}{\cos(\theta-\varphi)} \]

当 \(\cos(\theta-\varphi)\iff\theta=\varphi\) 时，\(F\) 取得最小值

\[F_{\min}=mg\sin(\varphi+\alpha) \]

全反力的应用

自锁问题

1.在机械设计中常用到下面的力学原理，如图所示，只要使连杆 \(AB\) 与滑块 \(m\) 所在平面间的夹角 \(\theta\) 大于某个值，那么，无论连杆 \(AB\) 对滑块施加多大的作用力，都不可能使之滑动，且连杆 \(AB\) 对滑块施加的作用力越大，滑块就越稳定，工程力学上称为“自锁”现象。设滑块与所在平面间的动摩擦因数为 \(\mu\)，为使滑块能“自锁”应满足的条件是（ ）
A.\(\mu\geq\tan\theta\)
B.\(\mu\geq\frac{1}{\tan\theta}\)
C.\(\mu\geq\sin\theta\)
D.\(\mu\geq\cos\theta\)

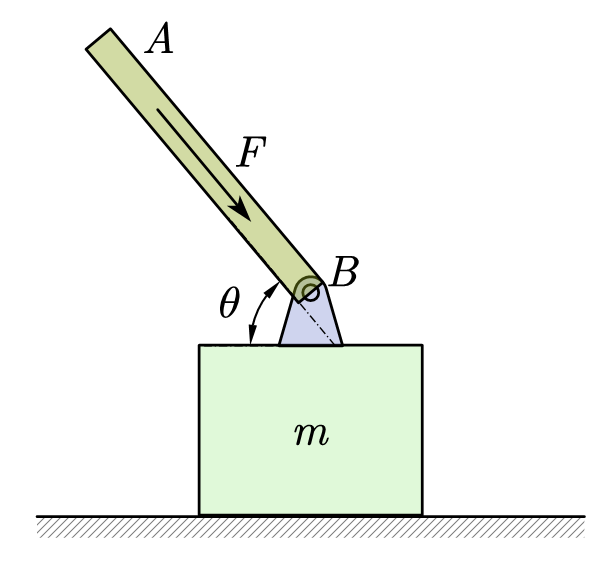
分析：滑块一直未滑动，即 \(f\leq f_{\max}=\mu N\)。且根据受力平衡可得 \(m\) 竖直方向受力的方程，与不等式联立即可求解。

解：对物体 \(m\) 受力分析，如图

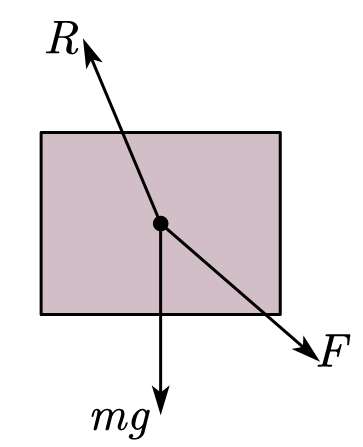
\(m\) 未能滑动，即地面对 \(m\) 的静摩擦始终未达到最大静摩擦 \(f_{max}\)

据此可列出不等式

\[f\leq\mu N \]

由 \(m\) 在水平、竖直方向平衡，得

\[N=mg+F\sin\theta\ \ \ \ \ ① \]

\[F\cos\theta=f\leq\mu N\ \ \ \ \ ② \]

联立①②式，消去 \(N\)，得

\[F(\cos\theta-\mu\sin\theta)\leq\mu mg \]

1°\(\cos\theta-\mu\sin\theta>0\)，即 \(\mu<\frac{1}{\tan\theta}\)

即满足

\[F\leq\frac{\mu mg}{\cos\theta-\mu\sin\theta} \]

时，滑块静止

与“\(F\) 无论多大，都无法使 \(m\) 滑动”矛盾

因此，该情况不成立

2°\(\cos\theta-\mu\sin\theta\leq0\)，即 \(\mu\geq\frac{1}{\tan\theta}\)

由于 \(\mu mg>0\)，此时，无论 \(F\) 取任何正实数，都小于等于 \(\mu mg\)

综上，

\[\mu\geq\frac{1}{\tan\theta} \]

注意：由于无法确定 \(\cos\theta-\mu\sin\theta\) 的符号，\(F(\cos\theta-\mu\sin\theta)\leq\mu mg\nRightarrow F\leq\frac{\mu mg}{\cos\theta-\mu\sin\theta}\)。

2.如图所示，质量为 \(m\) 的物体，放在一固定斜面上，当斜面倾角为 \(30^{\circ}\) 时恰能沿斜面匀速下滑。保持斜面倾角为 \(30^{\circ}\)，对物体施加一水平向右的恒力 \(F\)，使物体沿斜面匀速向上滑行（设最大静摩擦力等于滑动摩擦力）。若增大斜面倾角，当倾角超过某一临界角 \(\theta_0\) 时，则不论水平恒力 \(F\) 多大，都不能使物体从静止开始沿斜面向上滑行，已知重力加速度为 \(g\)，试求：
(1)物体与斜面间的动摩擦因数 \(\mu\)．
(2)水平恒力 \(F\) 的大小．
(3)这一临界角 \(\theta_0\) 的大小．

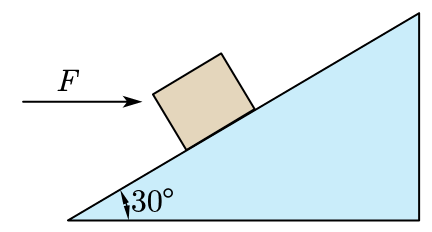
解：(1)对物体 \(m\) 自由下滑时受力分析，如图

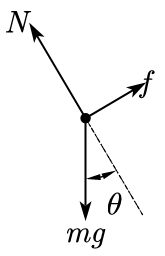
由 \(m\) 受力平衡，得

\[mg\sin30^{\circ}=\mu mg\cos30^{\circ} \]

解得

\[\mu=\tan30^{\circ}=\frac{\sqrt{3}}{3} \]

(2)对 \(F\) 作用下的 \(m\) 受力分析，如图

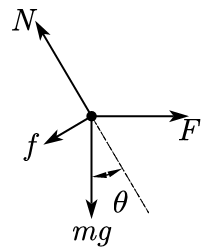
由 \(m\) 沿斜面方向受力平衡，得

\[\mu(mg\cos30^{\circ}+F\sin30^{\circ})+mg\sin30^{\circ}=F\cos30^{\circ} \]

解得

\[F=\frac{\mu mg\cos30^{\circ}+mg\sin30^{\circ}}{\cos30^{\circ}-\mu\sin30^{\circ}}=\sqrt{3}mg \]

(3)在临界角 \(\theta_0\) 时，\(m\) 始终保持静止

即

\[f\leq\mu N\ \ \ \ \ ① \]

对 \(m\) 受力分析，如图

\(m\) 沿斜面方向受力平衡，所以

\[f+mg\sin\theta_0=F\cos\theta_0\ \ \ \ \ ② \]

联立①②式，得

\[F\cos\theta_0-mg\sin\theta_0\leq\mu(mg\cos\theta_0+F\sin\theta_0) \]

即

\[F(\cos\theta_0-\mu\sin\theta_0)\leq mg(\mu\cos\theta_0+\sin\theta_0)\ \ \ \ \ ③ \]

1°\(\cos\theta_0-\mu\sin\theta_0>0\)，即 \(\mu<\frac{1}{\tan\theta_0}\)

\[③\iff F\leq \frac{mg(\mu\cos\theta_0+\sin\theta_0)}{\cos\theta_0-\mu\sin\theta_0} \]

满足上式时，\(m\) 静止

与“无论 \(F\) 取任何正实数，\(m\) 均静止”矛盾

2°\(\cos\theta-\mu\sin\theta_0\leq0\)，即 \(\mu\geq\frac{1}{\tan\theta_0}\)

此时无论 \(F\) 取任何值，均有

\[F(\cos\theta_0-\mu\sin\theta_0)\leq0<mg(\mu\cos\theta_0+\sin\theta_0) \]

满足题意

综上所述，满足题目的条件为

\[\mu\geq\frac{1}{\tan\theta_0}\iff\tan\theta_0\geq\frac{1}{\mu}=\sqrt{3} \]

所以，临界角

\[\theta_0=\frac{\pi}{3} \]

整体隔离中的全反力应用

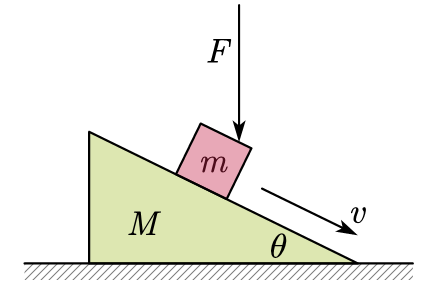
一物块恰能在一个斜面体上沿斜面匀速下滑，在其匀速下滑的过程中突然给它施加一个竖直向下的恒力 \(F\)，斜面仍静止不动．则物块在下滑过程中（ ）
A.物块匀加速下滑，地面不给斜面体摩擦力
B.物块匀加速下滑，地面给斜面体摩擦力
C.物块匀速下滑，地面不给斜面体摩擦力
D.物块匀速下滑，地面给斜面体摩擦力