算法优化》关于1D*1D的DP的优化
关于这一主题的DP问题的优化方法，我以前写过一篇博客与其有关，是关于对递推形DP的前缀和优化，那么这种优化方法就不再赘述了。
什么叫1D*1D的DP捏，就是一共有N种状态，而每种状态都要N种决策，这就叫1D*1D的DP，对于这种DP一般来说状态的转移都是可以从O(N2)优化到O(NlogN)甚至O(N)的，那么，针对于不同的情况，也有不同的优化方法
经典模型一：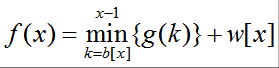
（b[x]随x非降）
对于DP方程形似与这一种的方程，明显的，这种DP的抉择方案数可以用单调队列直接解决化为O(1)，所以对于这样的转移方程复杂度就可以化为O(N)；
经典例题：POJ(2823)Sliding Window 给出友情链接刷题向》POJ2823 单调队列裸题（<不会做，请自裁>系列）
这道题无疑就是单调队列的最经典例题，那么用单调队列来解释也很容易。
接下来解释怎么用单调队列来维护这种题的最优最优决策数，
我们每次要做三个操作
1.将队首元素出队，直到队首元素属于b[x]~x-1
2.将队首元素作为最优解计算（由于单调队列的性质）
3.将g[x]加入队列，维护单调性
很容易得出复杂度为O(N)
经典模型二：
这种问题与决策单调性密切相关。那么什么是决策单调性捏？
当对于一个f(x)，决策g(a')比g(a)优，并且a'>a，那么对于任意的x'>x，决策g(a')仍然比g(a)优。 即∀a<=a'，g(a)<=g(a')；
显然的，并不是所有的方程都满足这一性质，首先我们先判断哪些DP方程有这一性质。
设s(x,i)为当判断到第x个，决策是第i个数时的函数值，s(x,i)=f(i)+w[i,x]；
那么也就是说：现在已知s(x,i')>=s(x,i) i'<i(式1)，试求满足s(x',i')>=s(x',i)(x<x')(式2)的条件；
我们先把式子打开，可以得到f(i')+w[i',x]>=f(i)+w[i,x](i'<i)，我们再把式子左边加上w[i',x']-w[i',x]，右边加上w[i,x']-w[i,x]，就可以得到式2；
那么显然，要这个不等式成立的条件就是w[i',x']-w[i',x]>=w[i,x']-w[i,x]；
将其整理得w[i',x']+w[i,x]>=w[i',x]+w[i,x'](i'>i，x'>x)；
归纳得出w[i+1,x+1]+w[i,x]>=w[i+1,x]+w[i,x+1]（四边形不等式）；
也就是说，只有在当前区间函数式满足以上结论时，我们的DP才可以使用抉择单调性优化。一般可以根据题目定义（或打表）判断；
经典例题：BZOJ1010玩具装箱（然而直到本篇博客发表时BZOJ还在维护）
经典模型三：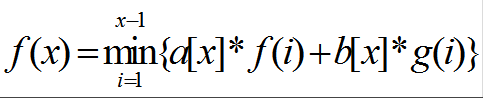
此问题因为在循环中的F是定值，所以可以转化为更加通用的方程：
得到这个式子之后，我们对这个式子进行一个处理，得到y(i)=-a(n)/b(n)*x(i)+f[n]/b(n);
对于这个式子，我们当前处理的就是用两个数组下标得出来的一元二次方程，那么对于每一个当前要决策的点x，a[x]和b[x]都是固定的，那么对于以上的一元二次方程，斜率都是一定的，那么也就是说，我们只要找到以前的，能使f[n]最大的点就好了。
那么我们可以把以前加入的点的x[n]和y[n]值作为平面上的点，既然有斜率，那么找截距就变成一个十分简单的事情了，只要找到能使截距最大的点就好。
然后我们会发现，我们能求到的最优解一定在这些点形成的上或下凸壳上，然后我们的问题就变成了维护凸壳。
这里有两种情况，
一种情况是这些直线的斜率和在横坐标上的点都是递增的，
在这种情况下，我们维护凸壳可以用单调队列处理，然后移动最优点的位置也是O(1)的，所以最好复杂度就是O(N)的
经典例题：BZOJ1597(土地购买)
还有一种情况，当斜率和横坐标没有任何限制，那么我们就不得不用平衡树叠二分来维护凸壳，这样复杂度就是O(NlogN)的。
经典例题：NOI2007国币兑换
关于这种题目暂时就说这么多，到以后或许会更新代码
