September's Summary

September's Summary

记录了这段时间里做的重要题。

9.1

P7602 [THUPC 2021] 视频倍增期 - 洛谷

让你求对于使 \(x_i\) 达到 \(\frac{x_i}{2}\) 的时间。

想了一会，主要是对于区间的操作，因为之前没有学过区间动态开点的线段树，所以犹豫了一会儿。

需要写标记永久化。

P2056 [ZJOI2007] 捉迷藏 - 洛谷

新知识：线段树动态维护直径。

这个题可以使用好几种方法：

1. 贪心，直接按照下标建线段树，区间最远一定是子区间最远的四个端点之二。
2. 括号序列，但我只会写九个标记的写法。
3. 树链剖分、\(LCT\) 动态维护（这种写法支持边权）
4. 淀粉质（太难了）

9.2

P4735 最大异或和 - 洛谷

可持久化 \(Trie\)。

建树的过程基本上和主席树类似，相当于每个下标放一个 \(root\)。

转换为前缀异或和，问题变成区间最大异或和。

普通 \(Trie\) + 回滚莫队可能也可以做，复杂度多了 \(\log\)，过不去。

P3674 小清新人渣的本愿 - 洛谷

感觉在哪里做过类似的题，一会儿就切了。

莫队 + \(bitset\)。

9.3

P7560 [JOISC 2021] フードコート (Day1) - 洛谷

注意到离开事件特别的烦人，于是有

\[离开人数 = 总加入人数 - 当前人数 \]

当前人数为区间减，区间推平取 \(\max{(a_i,0)}\)。

这样，对于每个查询，挂到下标上，查询当前加上删掉的。

对进队操作做扫描线。

P7561 [JOISC 2021] 道路の建設案 (Road Construction) (Day2) - 洛谷

曼哈顿转切比雪夫。

考虑二分答案，判定有多少对距离小于等于 \(mid\)，也就相当于两维的距离差都小于等于\(mid\)。

直接按照第一维排序，用双指针维护当前 \(x\) 合法的数，然后暴力加入 \(y\) 合法的数。如果你发现超过了 \(k\) 个就停止。

于是你判定一次就是 \(O(n\log n)\) 量级的。

二分答案，变为 \(O(n\log^2 n)\)。

9.4

P4097 【模板】李超线段树 / [HEOI2013] Segment - 洛谷

李超线段树，主要维护有斜率的线段凸包。

可用于斜率优化。

核心思想：每个线段树的节点取最大值、最小值。

P4655 [CEOI 2017] Building Bridges - 洛谷

斜率优化的李超线段树。

9.5

P3527 [POI 2011] MET-Meteors - 洛谷

很显然我们有主席树 + 直接二分的做法，但空间复杂度和时间复杂度不优秀。

二分答案的思想是取出当前答案区间的中间值进行验证，如果比答案小，则让答案的区间的左端点为中间值加一，反之让答案的右端点为中间值。按照二分答案的思想，我们也进行中间值验证。看例题，我们思考怎么验证。

对于当前答案区间 \([l,r]\)，我们把第 \([l,mid]\) 场流星雨全部落下，看在当前答案区间所 \([l,r]\) 属的所有询问是否在第 \([l,mid]\) 场流星雨下过之后已经收集足够的陨石，如果当前询问已经收集够，我们把它归为答案区间 \([l,mid]\) 中，反之我们把它归为答案区间 \([mid+1,r]\) 中，并且对于归为答案区间 \([mid+1,r]\) 的询问我们需要进行修改，对于其希望要收集的陨石数要减去 \([l,mid]\) 场流星雨的陨石总数，此处理解一下。

现在解决一下上面留下的问题，我们怎么能将答案都在 \([x,y]\) 区间的所有询问都放在一起呢？我们对于每一次划分，都将这些询问进行拷贝，并且修改，然后重新按左右排布，这样我们就能让这些答案在同一区间的询问在一起了。

P3332 [ZJOI2013] K大数查询 - 洛谷

我们设尚未解决的操作区间为 \([ql,qr]\)，答案区间为 \([l,r]\)，令当前答案为 \(mid\)。

则若该操作是添加操作，如果其添加的 \(C<=mid\)，这此次操作对于左子区间有贡献，加入左子区间中，并将区间线段树中的区间 \([q[i].l,q[i].r]\) 整体加 \(1\)。

反之，则将操作加入到右子区间中。

展示模板代码。

void solve(int l,int r,int x,int y){
	if(x>y) return;
	if(l==r){
		for(int i=x;i<=y;i++) if(Q[i].op==2) ans[Q[i].id] = l;
		return;
	}
	int mid = (l+r)>>1,tl = 0,tr = m;
	for(int i=x;i<=y;i++){
		if(Q[i].op==1){
			if(Q[i].k>mid){
				S.update(1,1,n,Q[i].L,Q[i].R,1);
				tQ[++tr] = Q[i];
			}
			else tQ[++tl] = Q[i];
		}
		else{
			int val = S.query(1,1,n,Q[i].L,Q[i].R);
			if(val<Q[i].k){
				Q[i].k -= val;
				tQ[++tl] = Q[i];
			}
			else tQ[++tr] = Q[i];
		}
	}
	for(int i=n+1;i<=tr;i++) if(tQ[i].op==1) S.update(1,1,n,tQ[i].L,tQ[i].R,-1);
	for(int i=1;i<=tl;i++) Q[x+i-1] = tQ[i];
	for(int i=m+1;i<=tr;i++) Q[x+tl+i-m-1] = tQ[i];
	solve(l,mid,x,x+tl-1),solve(mid+1,r,x+tl,y);
}

9.8

P1527 [国家集训队] 矩阵乘法 - 洛谷

整体二分的经典例题

对于单个询问，我们可以二分值域求出答案，但是复杂度是 \(Θ(n2m\log n)\) 的

不妨考虑将这若干个询问一起二分，统计在 \([l,mid]\) 的值有多少个，然后与询问的排名 \(k\) 进行比较，如果 \(≥k\) 则递归到左区间，否则将 \(k\) 修改并递归到右区间

• 注意不要直接二分值域，可以离散化后二分
• 统计矩阵中 \([l,mid]\) 的数有多少个时，可以用 \(vector\) 记录一下值为 \(val\) 的坐标都有哪些，然后直接扫就行了

P8868 [NOIP2022] 比赛 - 洛谷

维护区间历史和，贡献很难拆，标记也很难维护，线段树理论的巅峰。

9.9

P4364 [九省联考 2018] IIIDX - 洛谷

首先是55分的贪心，对于任何一个点i它的权值一定小于 \(\operatorname{floor}(i/x)\)。

这样就构成了一个树形结构，把所有的数全存进一个堆中，直接 \(dfs\) 回溯的时候把最大值赋给那个点就行了。

P5905 【模板】全源最短路（Johnson） - 洛谷

迪杰斯特拉竟然可以跑负权图！！！！！

需要引入势的概念。

9.11

P5356 [Ynoi Easy Round 2017] 由乃打扑克 - 洛谷

思路很简单：区间修改使用普通技巧，对于区间第 \(k\) 大，二分答案，丢到数组里查排名。

机房笑传之卡卡常。

P4528 [CTSC2008] 图腾 - 洛谷

神仙题。

因为那个形状太抽象了，考虑容斥。

得到了比较满足偏序关系的形状，运用反复的修辞手法丢到树状数组里面查，写完了。

谁想得到容斥啊。

9.12

P10281 [USACO24OPEN] Grass Segments G - 洛谷

对于 \((l_i,r_i,k_i)\)，有 \((l_j,r_j)\) 满足条件当且仅当：

\[k_i \le \min(r_i,r_j)-\max(l_i,l_j) \]

相当于满足：

\[\begin{cases} k_i\le r_i-l_j \\ k_i \le r_j-l_i \\ k_i \le r_j-l_j\end{cases} \]

可以转化为：

\[\begin{cases} l_j \le r_i-k_i \\ r_j \ge l_i + k_i \\ r_j-l_j \ge k_i \end{cases} \]

近似三维偏序，可以使用 \(CDQ\) 分治。

P6526 「Wdoi-1」四重存在 - 洛谷

仍然起手就是曼哈顿转切比雪夫。

发现只查最大值是容易的，但是查询时有可能删掉一个点。

然后就卡住了。。。

可以用线段树动态维护最近的点对，当然是切比雪夫。

9.15

P5596 【XR-4】题 - 洛谷

数学题。

首先判断无限解情况，将 \(x\) 移到右边，显然当 \(x^2+ax+b\) 为完全平方，即 \((\frac a2)^2=b\) 时有无数解。当然，为了避免精度误差，可以将它写成 \(a^2=4\times b\)。

然后来考虑怎么解此题，我们将左式因式分解，得：

\[(y-x)(y+x)=ax+b \]

令 \(k=y-x\)，原式可以化为：

\[k\times (k+2x)=ax+b \\ k^2+2xk=ax+b \\ 2xk-ax=b-k^2 \\ x(2k-a)=b-k^2 \\ x=\frac{b-k^2}{2k-a} \]

然后我们就可以枚举 \(k\) 了。由于 \(b-k^2\) 单调减，\(2k-a\) 单调增，那么有一个时刻会是 \(2k-a>0\) 且 \(b-k^2<0\)，此时可以退出循环。答案合法的条件是 \((2k-a)|(b-k^2)\)。

P2490 [SDOI2011] 黑白棋 - 洛谷

第一眼可以看出模型是 \(K-Nim\) 博弈。

因为结论是让每一位异或和模 \(K\) 为 \(0\)，所以在每个数位上组合计数。

感觉学到很多思维方法和 \(DP\) 技巧。

9.16

P3480 [POI 2009] KAM-Pebbles - 洛谷

假设我先手，那么我可以按照必胜策略把奇数堆中的石子转移到偶数堆，当对方拿的时候我们分情况讨论：

1. 对方拿奇数堆中的石子到偶数堆，相当于进行对于奇数堆的普通nim，我们继续按照必胜策略拿奇数堆中的石子；
2. 对方把偶数堆的石子拿到奇数堆，则我们可以把这部分石子继续向下拿，对于奇数堆相当于局势没有变动。

这个题就是以上 \(Nim\) 游戏的变种，差分一下即可。

P6487 [COCI 2010/2011 #4] HRPA - 洛谷

显然先手可以第一次直接取完获胜，但大多数情况下这么做并不是最少的。下面我们考虑第一次不取完的情况。

Wikipedia 中对齐肯多夫定理的描述：

任何正整数都可以表示成若干个不连续的斐波那契数之和。

这种和式称为齐肯多夫表述法。

构造这种和式可以通过每次贪心选出最大的不超过它的斐波那契数。

• 若正整数 \(n\) 为斐波那契数，得证。

• 否则

  • 先取 \(Fib_{t_1}\)，其中 \(t1\) 满足 \(Fib_{t_1} < n < Fib_{t_{1} + 1}\)。

  • \(n'=n - Fib_{t_1}\)，同上一步取出一个 \(Fib_{t_2}\) 满足 \(Fib_{t_2} < n' < Fib_{t_{2} + 1}\)。

  • 只要证 \(t_1 ≠ t_2 + 1\)。考虑反证法：

    • 假设 \(t_1 = t_2 + 1\)，则第一步取出的应当是 \(t_1 + 1\) 而不是 \(t_1\)。原因是 \(Fib_{t_1 + 1} = Fib_{t_1} + Fib_{t_1 - 1}\)。

如果正整数 \(n\) 为斐波那契数，则先手必败。

设 \(n = Fib_{t}\)，我们把 \(n\) 看成 \(Fib_{t-1}\) 和 \(Fib_{t-2}\) 两堆。

• 若第一步取的个数超过 \(Fib_{t-2}\)，则后手可以直接取完剩余石子。

• 否则，该问题变成了一个 \(n' = Fib_{t-2}\) 的规模更小的同样的问题。

考虑 \(n = 2\) 的情况（即规模最小的情况），先手只能取 \(1\)，于是后手取 \(1\) 获胜。

如果正整数 \(n\) 不为斐波那契数，则将其用齐肯多夫表示法表示后，最小的那一堆个数即为答案。

\(n = f_1 + f_2 + ... + f_k\)

先手取完最小的那一堆（即 \(f_k\)）后，根据齐肯多夫定理，\(f_{k-1} > 2 \times f_k\)，于是后手无法一次性取完次小的那一堆。再根据引理 1，次小的一堆的最后一块石子一定还是由先手取到，于是先手一定能取到最大的那一堆的最后一块，即整堆石子的最后一块。

P8346 「Wdoi-6」最澄澈的空与海 - 洛谷

让你求二分图是否有唯一匹配。

对于度为 \(1\) 的边，强行匹配。

第二选择节点数为 2 时的情况，所以一定也有第二种解法。

类似拓扑排序，将入度为 \(1\) 的点入队。

9.17

P3769 [CH弱省胡策R2] TATT - 洛谷

暴力可以过，所以就乱搞了。

当然题目非常的板子，就只是四维偏序 \(DP\)，可以用 \(CDQ\)，也可以 \(k-D\ Tree\)。

P4184 [USACO18JAN] Sprinklers P - 洛谷

首先，我们先根据样例画一幅图：

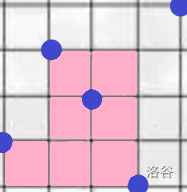
其中，粉色格子是肥料和水全喷到的地方。

我们发现，对于一行里面，粉色格子的左界是在这一行上面的所有蓝点中，最靠左的那一个，而右界是在这一行下面的所有蓝点中，最靠右的那一个。

我们接下来考虑如何对于一行求答案。设每一行的左界是 \(dw_i\)，右界是 \(up_i\)。

则我们将第\(i\)行当作矩形下界，枚举一个 \(j\leq i\) 当作矩形上界。则矩形左界是 \(dw_j\)，右界是\(up_i\)。设 \(L=dw_j,R=up_i\)，则以 \(i\) 为下界，\(j\) 为上界的矩形的方案数为\(\dfrac{(R-L)(R-L+1)}{2}\)。

这样预处理出来 \(up\) 和 \(dw\) 后，枚举 \(i\) 和 \(j\)，复杂度就是\(O(n^2)\)的。

然后，考虑优化。

当\(i\)增加的时候，最大的有 \(L\leq R\) 的 \(j\) 也是递增的。因为对于 \(\dfrac{(R-L)(R-L+1)}{2}\) 差分后，得到 \(\dfrac{(R-L)(R-L+1)}{2}=\sum\limits_{i=0}^{R-L}i\)，因此我们可以通过差分地更新它。

具体地说，我们设两个值 \(k\) 和 \(l\)，其中 \(k=\sum\limits_{q=j}^{i}R_q-L_q\)，\(l=\sum\limits_{q=j}^{i}\dfrac{(R_q-L_q)(R_q-L_q+1)}{2}\)。

则，当 \(R\) 减小 \(1\) 时，有 \(l\) 减小 \(k\) 和 \(k\) 减小 \((i-j+1)\)。

因此就可以差分地在 \(O(n)\) 时间内完成。

9.18

P7528 [USACO21OPEN] Portals G - 洛谷

那么很显然， 你可以从 \(p_1v_1\) 进入到达 \(p_2v_1,p_2v_2\) 这两个位置, 但是你无法到达 \(p_2\) 的另外两个位置。

那么怎么办呢？

没错，就是通过改变传送门的位置从而使所有的位置组成一个连通块。很显然图中存在两个环， 我们需要将它变成一个环，那么就可以达到目的了。

P4188 [USACO18JAN] Lifeguards S - 洛谷

动态开点线段树，关于区间覆盖的标记特别有意思。

9.19

P3401 洛谷树 - 洛谷

树上简单路径操作，想到树链剖分，差分也是显然的。

转化结论：二进制每一位上的每一位异或，如果有贡献，那就是 \(1\) 匹配 \(0\)。

P5354 [Ynoi Easy Round 2017] 由乃的 OJ - 洛谷

首先需要做起床困难综合症。

z.ans0 = (~x.ans0 & y.ans0) | (x.ans0 & y.ans1);
z.ans1 = (~x.ans1 & y.ans0) | (x.ans1 & y.ans1);

按照上面的方式合并左右儿子的值就行了。

树剖比较难写，\(LCT\) 比较小清新。

9.24

P2934 [USACO09JAN] Safe Travel G - 洛谷

最短路树。

最短路的更新可以看成一棵树。

样例的图画出来是这样：

既然最短路唯一，我们可以记录 1 节点到每个节点的最短路的最后一条边的起点，也就是最后一个松弛它的节点，作为它的父亲，构造出一棵根为 1 号节点的最短路树。因为最短路唯一，最短路树也是唯一的。

由样例构造出的最短路树是这样的：

红色边为最短路树上的边，黑色边不属于最短路树，我们将不属于最短路树的边称为非树边。为了方便，我们把树边标记为红色，非树边为黑色。

根据最短路树的性质，在断开 i 节点到它父亲的边后，最短路一定会经过至少一条非树边，而且仅经过一条非树边，因为如果该路径经过多条非树边，那么总有一条非树边可以用最短路树上的一条不包含被断开边的链替代。

P10013 [集训队互测 2023] Tree Topological Order Counting - 洛谷

树上拓扑计数的结论，参见附录。

有两种写法，一种是求子树内的拓扑贡献，一种更妙的思路是维护的是所有不在 \(u\) 子树内的节点的相对拓扑序。

树上 DP 好题。

和顺序有关的问题，在 DP 状态设计时，如果整体不好考虑，可以考虑当前 DP 完的集合在离散化后的状态，转移时乘上组合数。

\(f_{u,i}\) 表示不考虑子树 \(u\) 内部，将 \(u\) 和子树 \(u\) 外的节点拓扑序离散化后，节点 \(u\) 的拓扑序为 \(i\) 的方案数。

则答案计算如下：

\[f_{v,i}=\sum\limits_{j=1}^{i-1} f_{u,j}\times \underbrace{\binom{(n-sz_u+1-i)+(sz_u-sz_v-1)}{sz_u-sz_v-1}}_{\text{第一部分}}\times \underbrace{\frac{(sz_u-sz_v)!}{\prod\limits_{x\in subtree_u\land x\notin subtree_v} sz_x}}_{\text{第二部分}} \]

\[ans_i=\sum\limits_{j=1}^n b_j\times f_{i,j}\times \underbrace{\binom{(n-sz_i-j+1)+(sz_i-1)}{sz_i-1}}_{\text{第一部分}}\times \underbrace{\frac{sz_i!}{\prod_{k\in subtree(i)} sz_k}}_{\text{第二部分}} \]

维护 \(g_u=\prod_{k\in subtree(u)} sz_k\)，即可 \(O(n^2)\) 计算答案。

9.25

P4513 小白逛公园 - 洛谷

动态维护最大子段和。

分为左最大、右最大、答案、求和四个 \(tag\)。

P14015 [ICPC 2024 Nanjing R] 生日礼物 - 洛谷

一开始想到的是从右向左拿一个单调栈维护，但是假了。

注意到有的地方可以合并，有的地方不行。

猜测和奇偶性相关。

通过查阅题解，我们得知偶数位取反即可贪心匹配，太妙了。

9.26

P4385 [CHCI 2009 Final Exam #2] DVAPRAVCA - 洛谷

计算几何+线段树好题。

给定 \(n\) 个红色或蓝色的点，三点不共线，求中间没有蓝点的两条平行线间最多能有几个红点。

显然，两条平行线一定不会是两点间的连线，否则将平行线旋转足够小的角度 \(δ\) 后可以得到另一个更优的解。

假设两条平行线都垂直于直线 \(l\)，过每个点作 \(l\) 的垂线，得到 \(n\) 个点，那么问题就转化为求投影序列上的最长连续红色子段。

P6845 [CEOI 2019] Dynamic Diameter - 洛谷

动态维护树的直径，树的形态不变。

使用九标记写法可以 \(AC\)。

附录

树上拓扑序计数

我也不知道这个东西该归到哪里。。

对于一棵树，我们可以对其进行拓扑排序，那么求总方案数。

解法一：

考虑每个节点及其子树的全排列，发现其拓扑序满足当前节点在第一个，子树内部排列中的 \(\cfrac{1}{siz_u}\) 种是合法的，固有 \(S = \cfrac{n!}{\prod_{u=1}^n siz_u}\)。

解法二：

考虑儿子之间随机排列，这正是多项式系数。

所以对于每一个节点，有 \(f_u = \dbinom{siz_u-1}{siz_{v1},siz_{v2},\dots,siz_{vk}} \prod_{v\in son_u} f_v\)。

化简式子：

\[\begin{align} f_u &= \dbinom{siz_u-1}{siz_{v1},siz_{v2},\dots,siz_{vk}} \prod_{v\in son_u} f_v \\ &= \frac{(siz_u-1)!}{\prod_{v\in son_u} siz_v} \prod_{v\in son_u} f_v \\ &= (siz_u-1)! \times \prod_{v\in son_u} \frac{f_v}{siz_v} \\ \end{align} \]

事实上，观察等式，是可以相消的。

\[S = \cfrac{n!}{\prod_{u=1}^n siz_u} \]

[ABC160F] Distributing Integers

裸的结论题。好吧并不是。

我们需要对于每个节点，以它为根，进行一次拓扑序计数，直接换根 \(DP\)。

CF1946E Girl Permutation

这只是一种方式，考察建模。

一些感想

主要研究了一下 \(ABC\) 写题法。

因为后面越学越难，对于思维过于难的题，很可能会卡住，因此需要更有效率的方法。

把题目分成 \(3\) 类：

1. 看了之后觉得有价值的题。
2. 看懂了思路但还不能清晰的反映到代码上的题。
3. 可以开始写代码的题。

每次在计划中选择任意一个马上可以开始完成的任务（哪一类都行）。

不会了就放下，不会耽误效率。

当然这样做也有一定的代价，思路不是很连贯。

所以有时候也会抽一整天的时间研究一个专题，让思路比较连贯。

反正各有取舍吧，两种方法合起来比较适合我的节奏。