洛谷P6619 [省选联考 2020 A/B 卷] 冰火战士

0x1f 关于被人类遗忘掉的一个 Trick

树状数组已经快被人们遗忘掉了。

出题人更不会卡常，线段树将要占领天下。

？

考生：怎么T了。

你永远也不会知道，2020年省选联考，是谁将线段树卡掉了，永远……

\[\large 树状数组二分/倍增 \]

由树状数组的定义可知，单点树状数组管辖长度为 \(lowbit(x)\)。

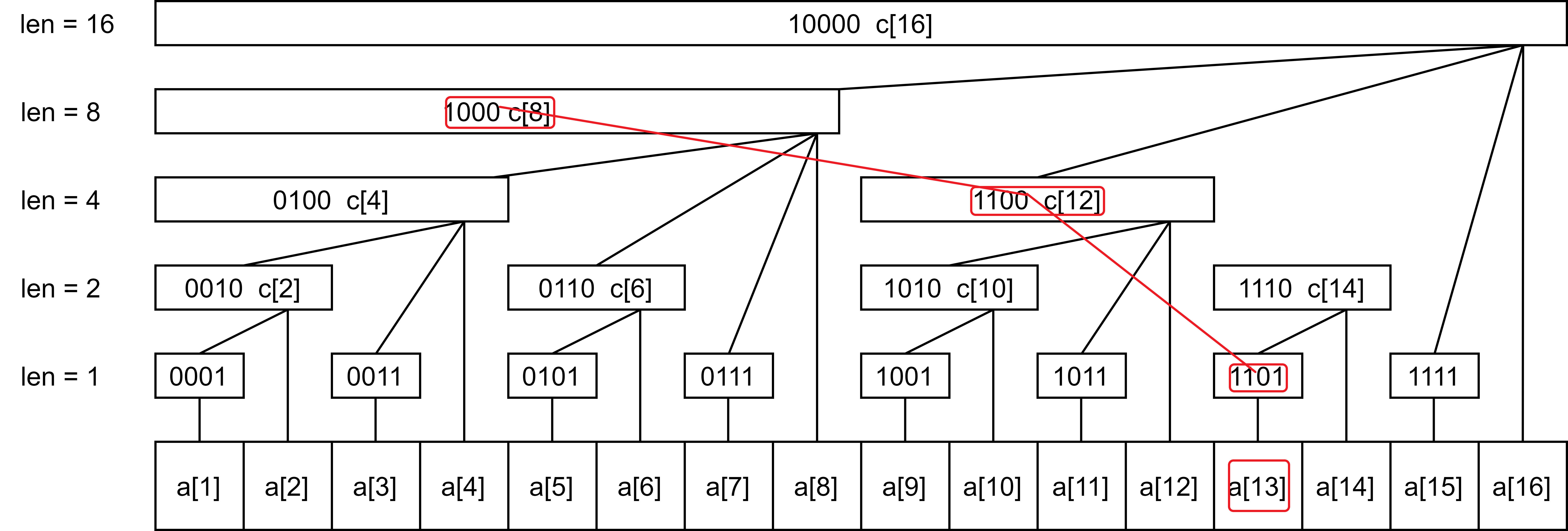
如果我们想逼近一个点，其前缀和为 \(k\)，我们可以按照上图红线的方式逼近（假设最后 \(a_{13}\) 前缀和为 \(k\)）。

代码展示出来像这样：

int pos = 0,sum = 0;
for(int i=21;~i;i--){
	if(pos+(1<<i)<=n && sum+tree[pos+(1<<i)]<k){
		pos += (1<<i);
		sum += tree[pos];
	}
}

\(pos\) 记录了最后的位置，\(sum\) 记录了前缀和（\(\le k\)）。

该技巧比较考验选手对树状数组的掌握与代码构想能力。

0x2f 关于本题的一些性质分析

简言之，我们有冰火两队，选定一个温度 \(T\)，大于等于 \(T\) 的所有火可以计入总和，小于等于 \(T\) 的所有冰可以计入总和。

最大化冰与火的最小值。

我觉得上一个图要直观一点。

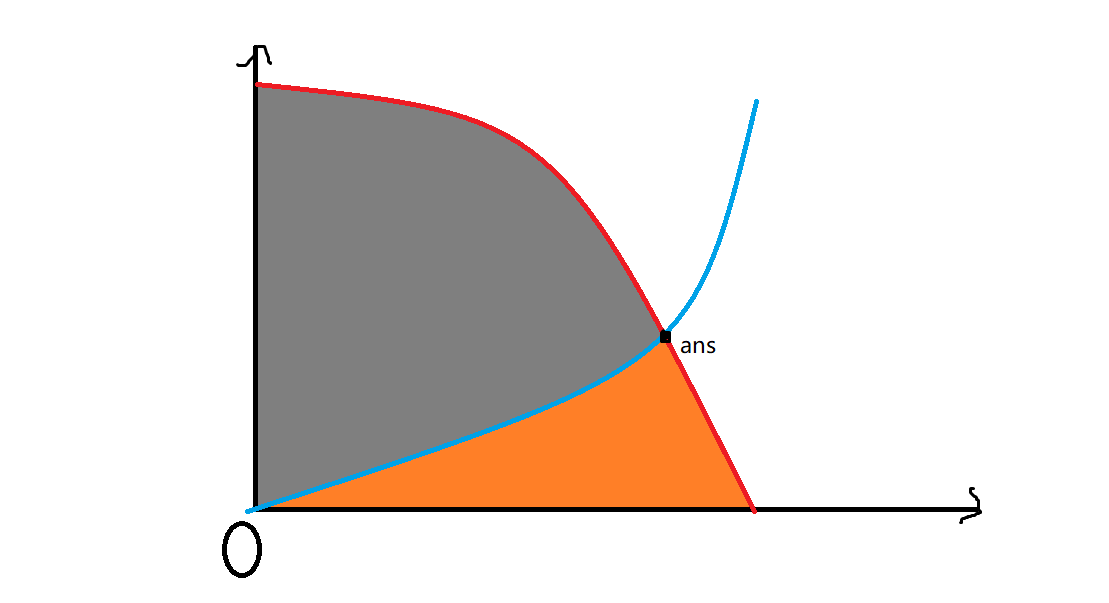
搬的图（逃

横轴就是 \(T\)，纵轴就是冰与火的数量啦。

显然数量相减是具有单调性的，考虑二分答案，再在树状数组上区间查询，有 \(O(n \log^2 n)\) 做法。

\(2e6\ VS \ 3s\)，显然 \(60pts\)。

计一类整体二分：

为什么可以优化？

因为每次计算会重复，如果每次像倍增一样越取越少，就不会超过答案，还不用重复计算。

所以，如果我们在树状数组上二分，可以做到 \(O(n \log n)\)。

具体到这道题，我们要让取到值的地方（如上上图中的 \(a_{13}\)）不能越界，且冰的前缀和永远不能超过火的后缀和，就可以树状数组二分了。

代码中还有一次二分，是为了求得最大温度。

\(\huge \mathscr{Code}\)

#include<bits/stdc++.h>
namespace Fread { const int SIZE = (1 << 18); char buf[SIZE], * p1 = buf, * p2 = buf; inline char getchar() { return (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, SIZE, stdin), p1 == p2) ? EOF : *p1++); } }
namespace Fwrite { const int SIZE = (1 << 18); char buf[SIZE], * S = buf, * T = buf + SIZE; inline void flush() { fwrite(buf, 1, S - buf, stdout), S = buf; }  struct NTR { ~NTR() { flush(); } }ztr; inline void putchar(char c) { *S++ = c; if (S == T) flush(); } }
namespace Fastio {
	struct Reader { template <typename T> Reader& operator >> (T& x) { char c = Fread::getchar(); bool f = false; while (c < '0' or c > '9') { if (c == '-') f = true; c = Fread::getchar(); } x = 0; while (c >= '0' and c <= '9') { x = (x << 1) + (x << 3) + (c ^ 48); c = Fread::getchar(); } if (f) x = -x; return *this; }Reader& operator>>(char& c) { c = Fread::getchar(); while (c == '\n' || c == ' ' || c == '\r')c = Fread::getchar(); return *this; }Reader& operator>>(char* str) { int len = 0; char c = Fread::getchar(); while (c == '\n' || c == ' ' || c == '\r')c = Fread::getchar(); while (c != '\n' && c != ' ' && c != '\r')str[len++] = c, c = Fread::getchar(); str[len] = '\0'; return *this; }Reader() {} }cin;
	struct Writer { template <typename T> Writer& operator << (T   x) { if (x == 0) return Fwrite::putchar('0'), * this; if (x < 0) Fwrite::putchar('-'), x = -x; static int sta[45], top = 0; while (x)  sta[++top] = x % 10, x /= 10; while (top)  Fwrite::putchar(sta[top] + '0'), --top; return *this; } Writer& operator<<(char c) { Fwrite::putchar(c); return*this; }Writer& operator<<(const char* str) { int cur = 0; while (str[cur])Fwrite::putchar(str[cur++]); return *this; }Writer() {} }cout;
}
#define cin  Fastio :: cin
#define cout Fastio :: cout
using namespace std;
const int N = 2e6+100;
int q,lsh[N],tot;
struct dat{
	int op,t,x,y;
}Q[N];
class FenwickTree{
	public:
		int tree[N],arr[N],sum;
		inline void update(int x,int v){
			sum += v;
			arr[x] += v;
			while(x<=tot) tree[x] += v,x += x&-x;
		}
		inline int query(int x){
			int ans = 0;
			while(x) ans += tree[x],x -= x&-x;
			return ans;
		}
}T[2];
int main(){
//	ios::sync_with_stdio(false);
//	cin.tie(0),cout.tie(0);
	cin>>q;
	for(int i=1;i<=q;i++){
		cin>>Q[i].op;
		if(Q[i].op==1){
			cin>>Q[i].t>>Q[i].x>>Q[i].y;
			lsh[++tot] = Q[i].x;
		}
		else cin>>Q[i].t;
	}
	sort(lsh+1,lsh+tot+1);
	tot = unique(lsh+1,lsh+tot+1)-lsh-1;
	for(int i=1;i<=q;i++) Q[i].x = lower_bound(lsh+1,lsh+tot+1,Q[i].x)-lsh+Q[i].t;
	for(int i=1;i<=q;i++){
		if(Q[i].op==1){
			T[Q[i].t].update(Q[i].x,Q[i].y);
		}
		else{
			T[Q[Q[i].t].t].update(Q[Q[i].t].x,-Q[Q[i].t].y);
		}
		int sIce = 0,sFire = T[1].sum,now = 0;
		for(int k=21;~k;k--){
			if(now+(1<<k)<=tot && sIce+T[0].tree[now+(1<<k)]<=sFire-T[1].tree[now+(1<<k)]){
				now += (1<<k);
				sIce += T[0].tree[now];
				sFire -= T[1].tree[now];
			}
		}
		int ans = sIce,ans2 = sFire - T[1].arr[now+1];
		if(ans2>=ans){
			ans = ans2,now = 0;
			sFire = T[1].sum;
			for(int k=21;~k;k--){
				if(now+(1<<k)<=tot && sFire-T[1].tree[now+(1<<k)]>=ans){
					now += (1<<k);
					sFire -= T[1].tree[now];
				}
			}
		}
		if(!ans) cout<<"Peace\n";
		else cout<<lsh[now]<<' '<<ans*2<<'\n';
	}
	return 0;
}