Gym104813K Omniscia Spares None

构造 \(n\) 个点的平面图，使得最多存在 \(4\) 个点度数小于 \(6\)。

\(1 \leq n \leq 100\)。

---

显然 \(n=1,2,3,4\) 时任意构造都是对的。

\(n=5,6\) 时所有点的度数都小于 \(6\)，显然无解。

不妨从 \(n = 7\) 来开始考虑，此时我们需要构造 \(3\) 个度数 \(\geq 6\) 的点。

不妨钦定 \(1,2,3\) 三个点度数 \(\geq 6\)，显然这三个点要连接所有点。

此时 \(4,5,6,7\) 四个点都要连接 \(1,2,3\)，三角形内和三角形外都最多只能有 \(1\) 个点。

也就是说 \(n=7\) 无解，考虑 \(n=8\)。

我们考虑构造的平面图边数应该尽可能多，不难想到类似三角剖分的形式。

考虑一种常见的三角剖分形式：

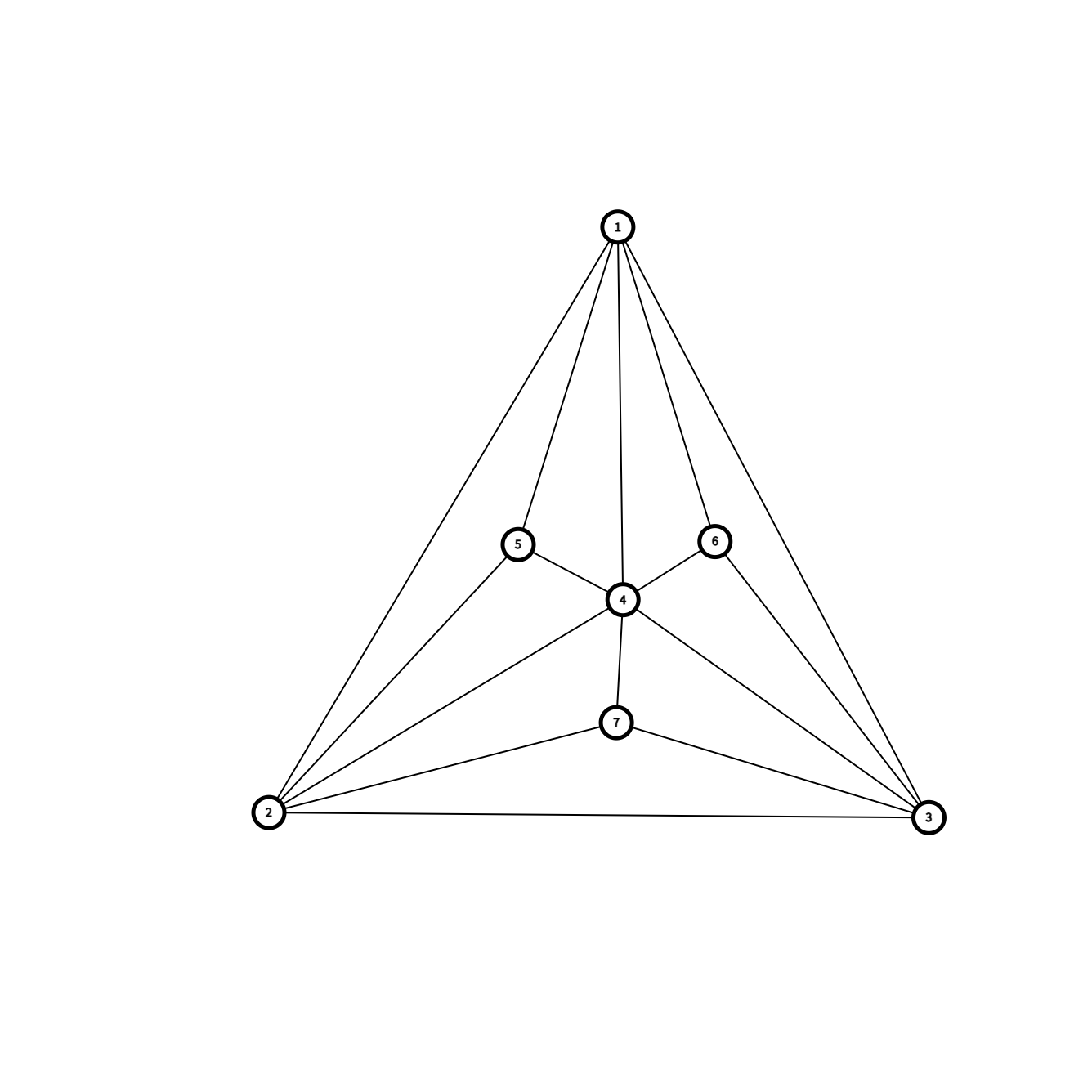
已经有一个点的度数为 \(6\) 了，剩下 \(3\) 个点度数为 \(5\)，\(3\) 个点度数为 \(3\)。

这是 \(n=7\)，现在需要新增一个点，多出三个度数 \(\geq 6\) 的点，不难想到：

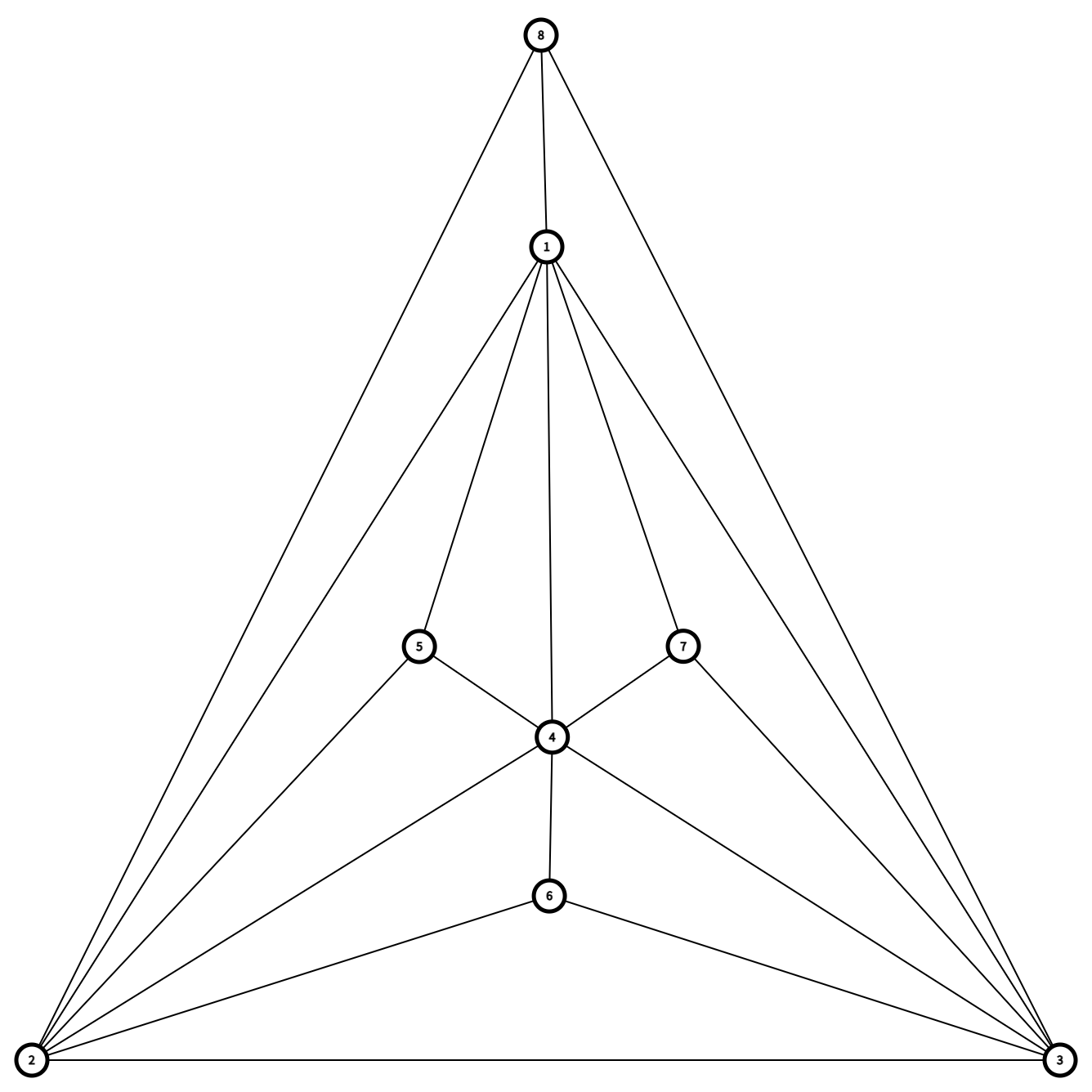
考虑上面不达标的点为 \(5,6,7,8\)，我们考虑构造类似的结构。

显然 \(5\) 和 \(7\) 的地位不可以改变，尝试改变 \(6\) 和 \(8\)。

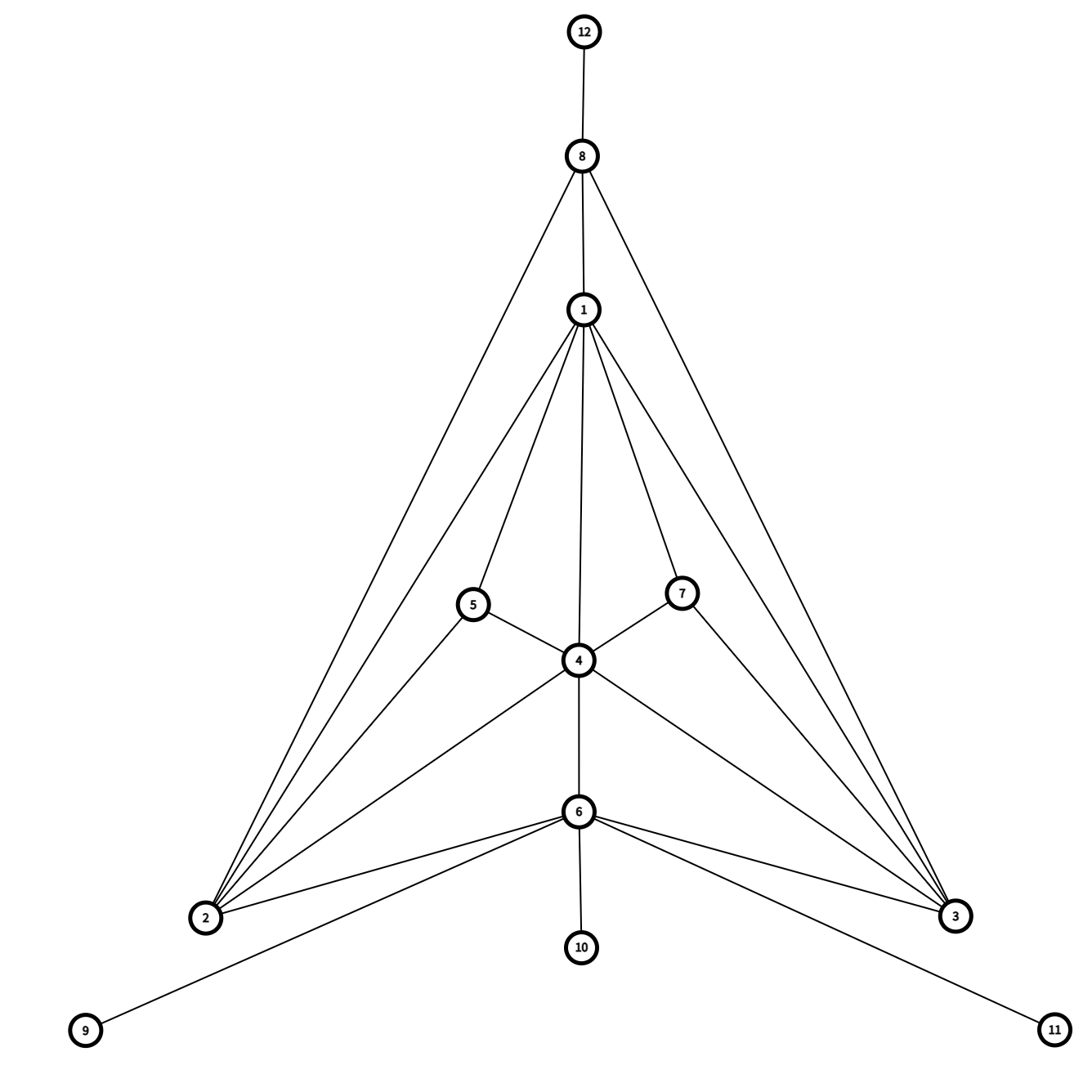
把能连的边给连上。

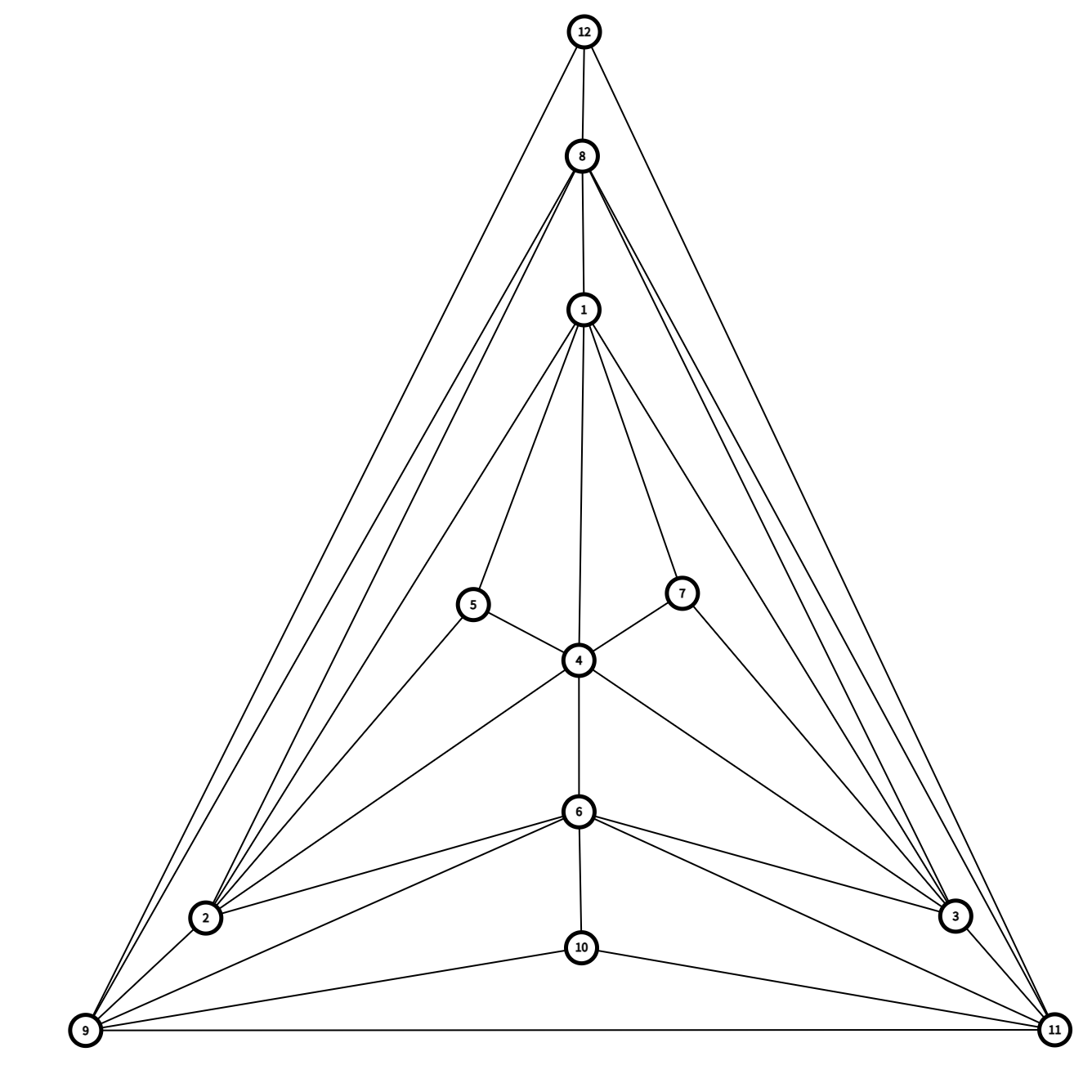
你发现这就对了，这就是 \(n=12\)。

同理可得 \(n=16\)。

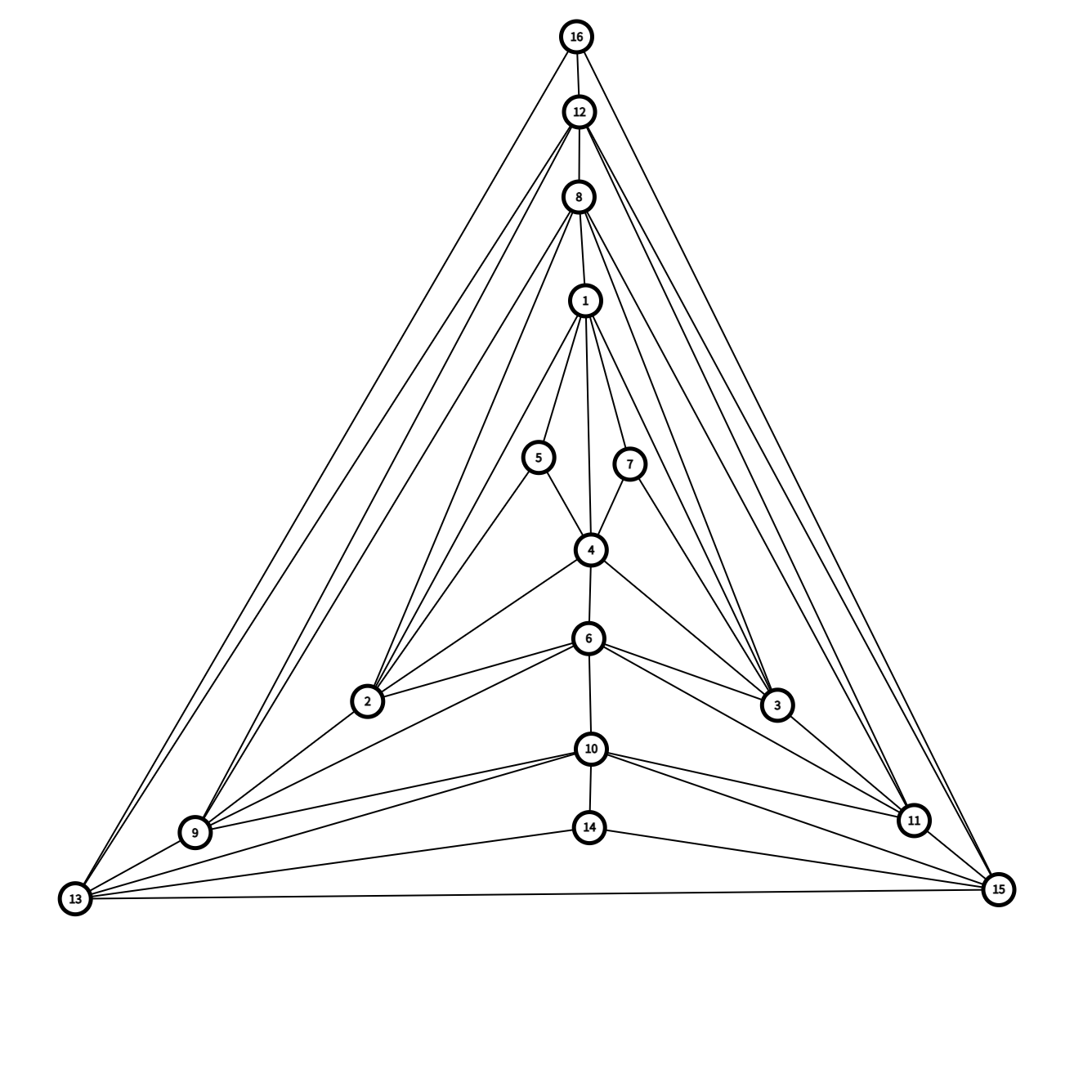
这个构造可以一直嵌套，我们就解决了 \(n=4k\) 的情况。

考虑还有什么东西是我们能够构造出来的。

首先我们发现所有点的度数都应该 \(\geq 3\)。

询问 deepseek 可知，\(n\) 个点的平面图边数最多为 \(3n-6\)。

也就是说，所有点的度数之和 \(\leq 6n-12\)，所以这个界是很紧的。

考虑利用仅有的 \(3\) 度点进行最大化的贡献，结合前面怎么对称怎么来的策略，得到：

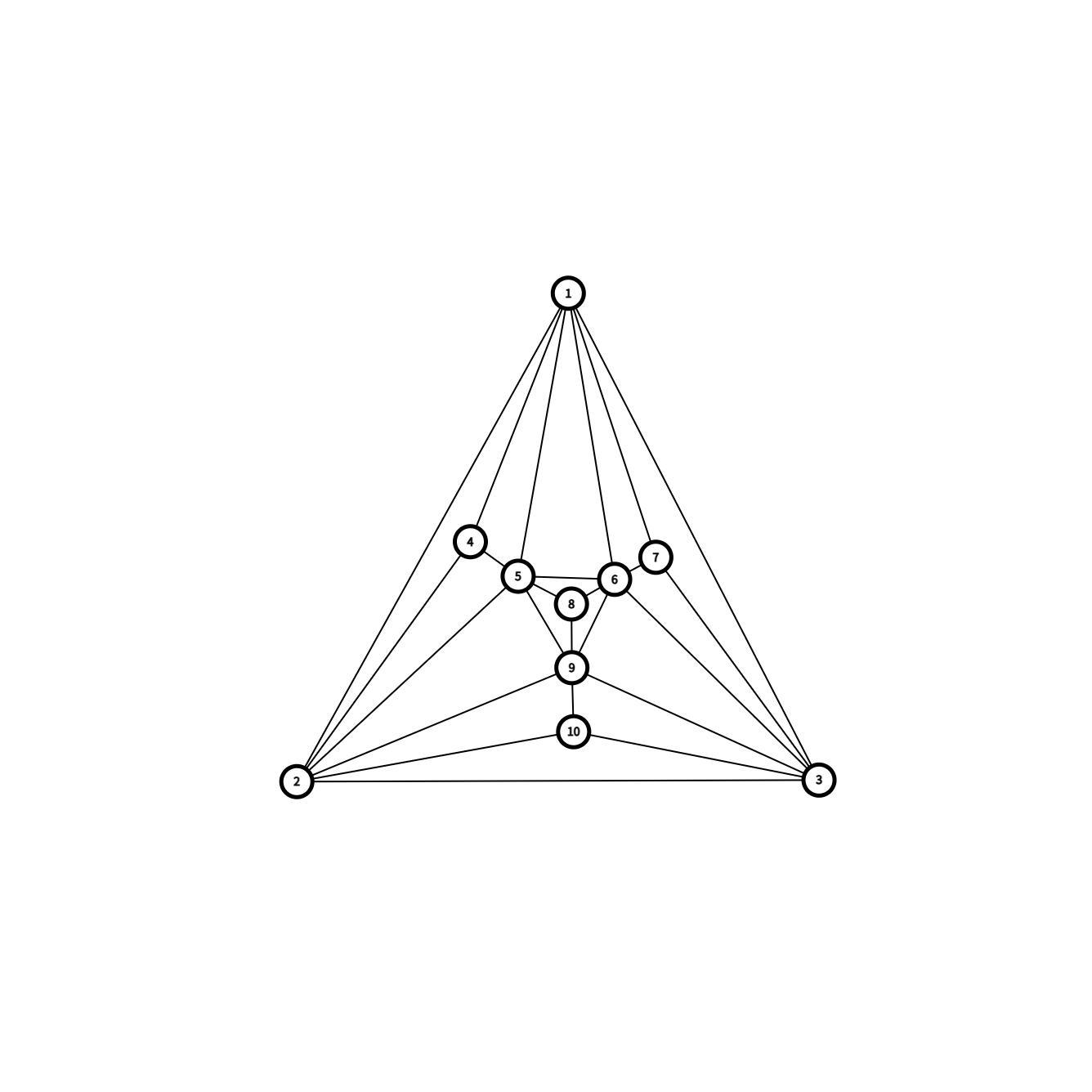
但是这个构造太对称了，不具有良好的可拓展性，我们考虑一些更牛的构造：

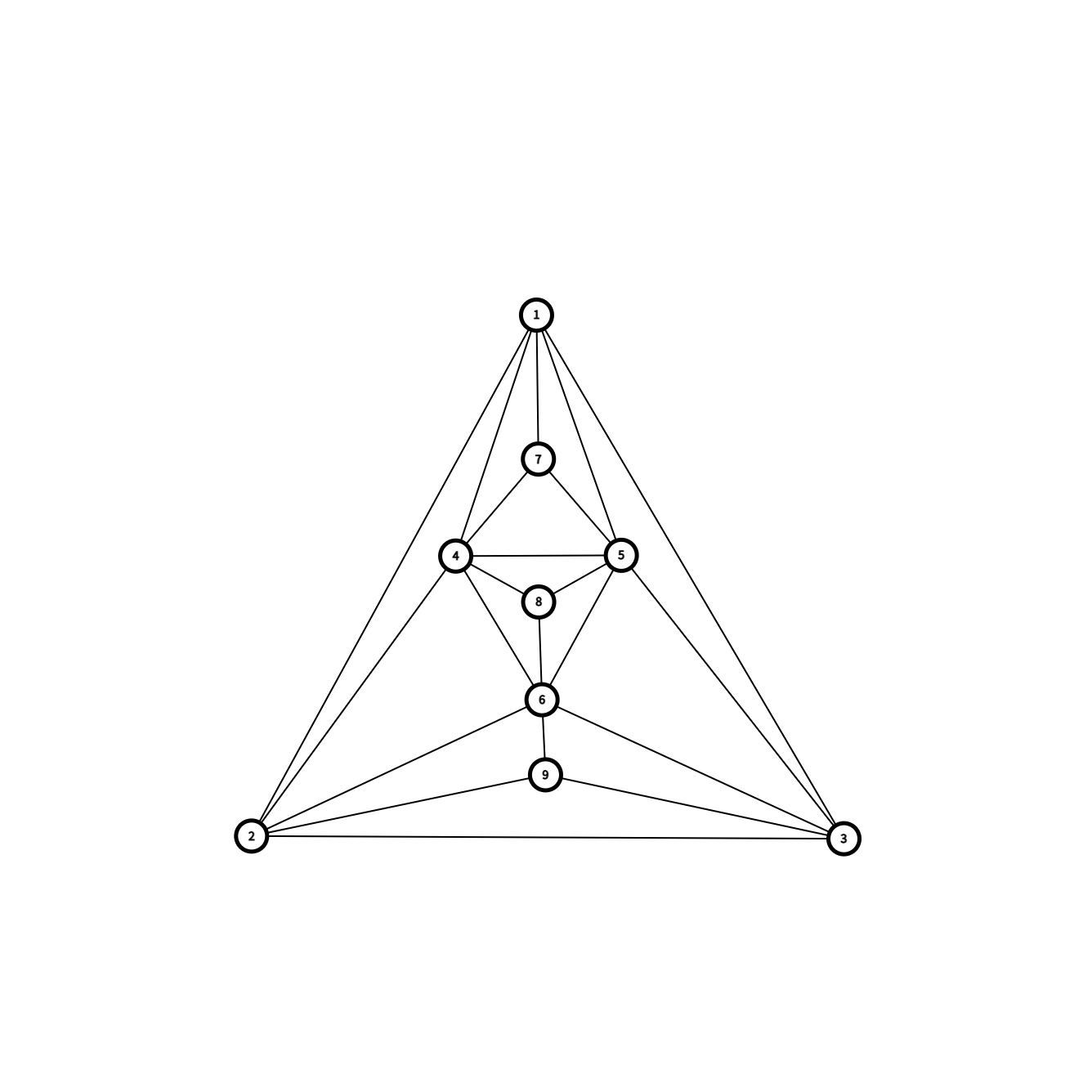
此时的构造中有六个点是不符合要求的，但是只要我们再加入一个点：

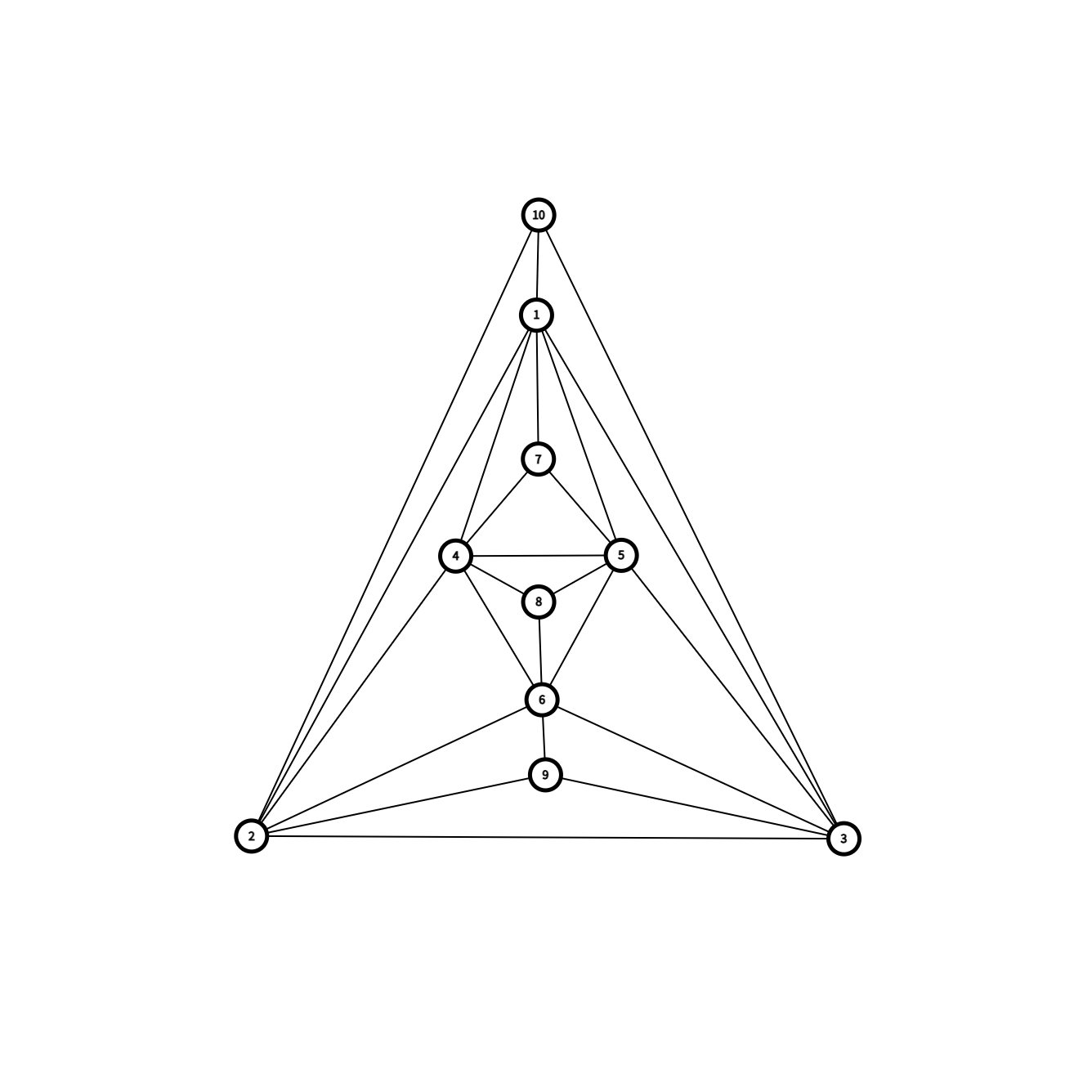
构造就正确了。同时你发现，此时不满足条件的点变成了 \(7,8,9,10\)。

考虑继续按照上面的想法，我们进行增量构造。

\(n=14\)：

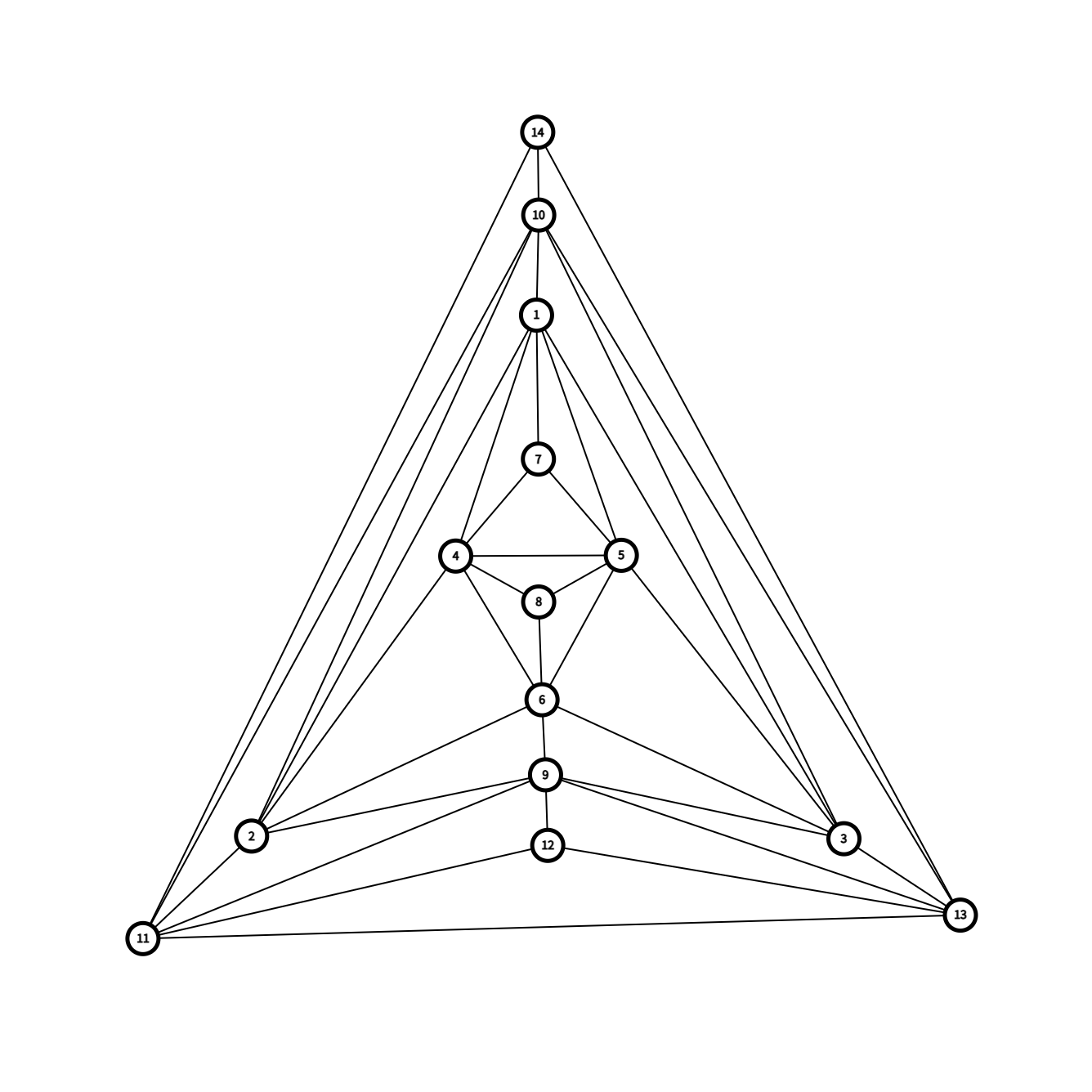
\(n=18\)：

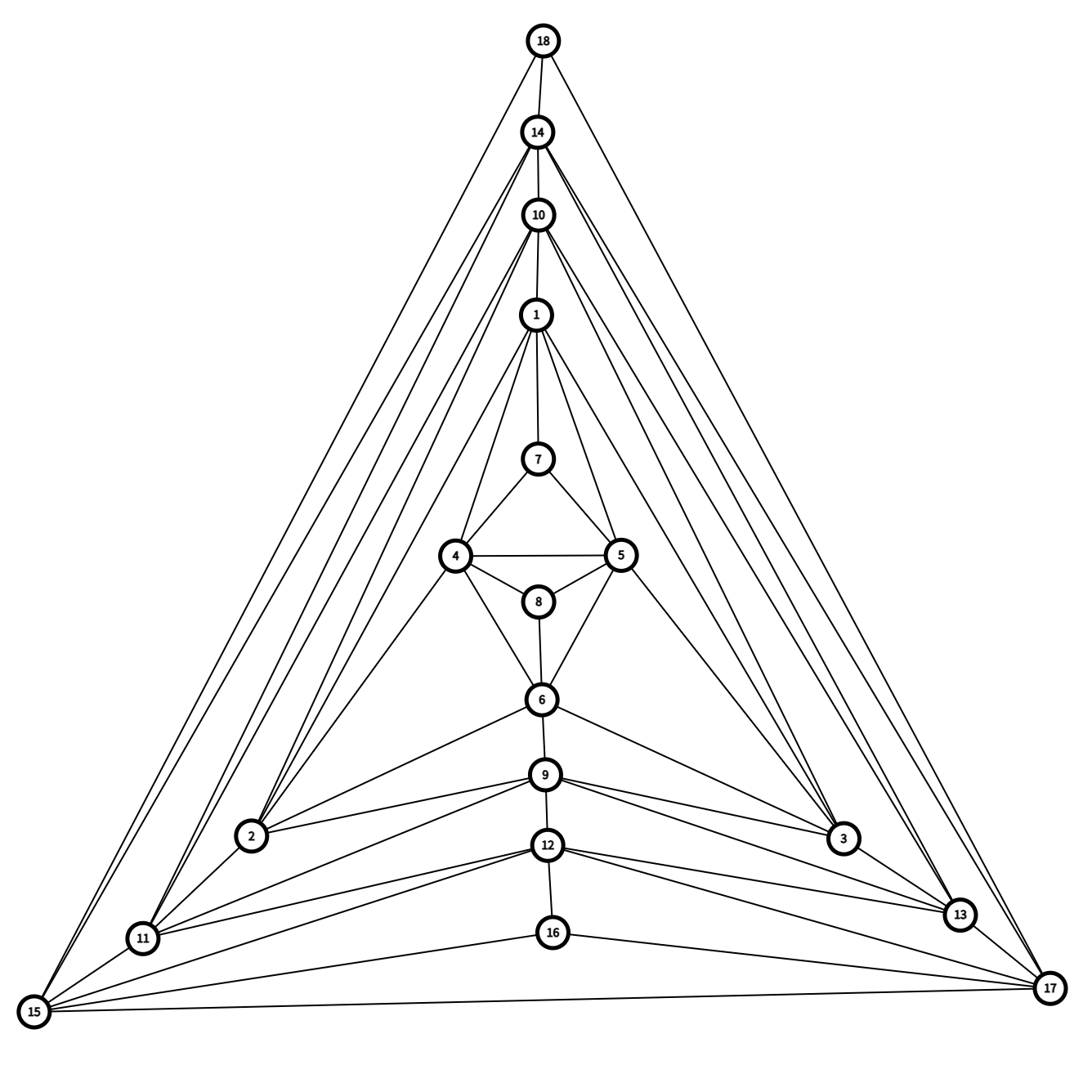
接下来我们就得到了 \(n=4k+2\) 的情况。

考虑 \(n\) 为奇数，显然此时我们不能是 \(6\) 度点加 \(3\) 度点的组合，此时是无解的。

虽然这不是严谨的证明，但是动动脑子会发现这确实无解。

//Ad astra per aspera
#include<iostream>
#include<cstdio>
using namespace std;
void Subtask1(int n){
	printf("Yes\n");
	for(int i=1;i<=n;i++){
		printf("%d %d\n",i,i);
	}
	printf("0\n");
}
void Subtask2(int n){
	printf("Yes\n");
	for(int i=1;i<=n;i++){
		int ord=i/4;
		if(i==1){
			printf("-1 1\n");
		}
		else if(i==3){
			printf("1 1\n");
		}
		else if(i%4==0){
			printf("0 %d\n",ord+2);
		}
		else if(i%4==1){
			printf("%d %d\n",-3-ord,-1-ord);
		}
		else if(i%4==2){
			printf("0 %d\n",1-ord);
		}
		else{
			printf("%d %d\n",3+ord,-1-ord);
		}
	}
	printf("%d\n",3*n-6);
	printf("2 1\n");
	printf("2 3\n");
	printf("2 4\n");
	printf("2 5\n");
	printf("2 6\n");
	printf("2 7\n");
	printf("1 4\n");
	printf("1 5\n");
	printf("3 4\n");
	printf("3 7\n");
	printf("6 5\n");
	printf("6 7\n");
	for(int i=4;i+4<=n;i++){
		printf("%d %d\n",i,i+4);
	}
	for(int i=5;i<=n;i+=4){
		printf("%d %d\n",i,i-1);
		printf("%d %d\n",i,i+3);
	}
	for(int i=7;i<=n;i+=4){
		printf("%d %d\n",i,i-3);
		printf("%d %d\n",i,i+1);
	}
	for(int i=9;i<=n;i+=4){
		printf("%d %d\n",i,i-3);
		printf("%d %d\n",i,i+1);
	}
	for(int i=11;i<=n;i+=4){
		printf("%d %d\n",i,i-5);
		printf("%d %d\n",i,i-1);
	}
	printf("%d %d\n",n-1,n-3);
}
void Subtask3(int n){
	printf("Yes\n");
	for(int i=1;i<=n;i++){
		int ord=i/4;
		if(i==1){
			printf("0 -1\n");
		}
		else if(i==3){
			printf("-1 0\n");
		}
		else if(i==5){
			printf("1 0\n");
		}
		else if(i%4==0){
			printf("0 %d\n",-1-ord);
		}
		else if(i%4==1){
			printf("%d %d\n",2+ord,-2-ord);
		}
		else if(i%4==2){
			printf("0 %d\n",2+ord);
		}
		else{
			printf("%d %d\n",-3-ord,-3-ord);
		}
	}
	printf("%d\n",3*n-6);
	printf("2 3\n");
	printf("2 5\n");
	printf("2 6\n");
	printf("3 5\n");
	printf("3 6\n");
	printf("5 6\n");
	printf("3 1\n");
	printf("1 5\n");
	printf("3 4\n");
	printf("4 5\n");
	printf("1 4\n");
	printf("3 7\n");
	printf("5 9\n");
	for(int i=7;i+4<=n;i+=4){
		printf("%d %d\n",i,i+4);
	}
	for(int i=4;i+4<=n;i+=4){
		printf("%d %d\n",i,i+4);
	}
	for(int i=9;i+4<=n;i+=4){
		printf("%d %d\n",i,i+4);
	}
	for(int i=6;i+4<=n;i+=4){
		printf("%d %d\n",i,i+4);
	}
	for(int i=7;i<=n;i+=4){
		printf("%d %d\n",i,i-1);
		printf("%d %d\n",i,i+3);
	}
	for(int i=9;i<=n;i+=4){
		printf("%d %d\n",i,i-3);
		printf("%d %d\n",i,i+1);
	}
	for(int i=7;i<=n;i+=4){
		printf("%d %d\n",i,i-3);
		printf("%d %d\n",i,i+1);
	}
	for(int i=9;i<=n;i+=4){
		printf("%d %d\n",i,i-5);
		printf("%d %d\n",i,i-1);
	}
	printf("%d %d\n",n-1,n-3);
}
void Subtask4(int n){
	printf("No\n");
}
int main(){
	int n;
	scanf("%d",&n);
	if(n<=4){
		Subtask1(n);
	}
	else if(n>=8  &&  n%4==0){
		Subtask2(n);
	}
	else if(n>=10  &&  n%4==2){
		Subtask3(n);
	}
	else{
		Subtask4(n);
	}
	return 0;
}