龙门考古

很久很久以前，有一个 \(1\) 到 \(n\) 的排列 \(A\)。

对于 \(1\) 到 \(n\) 的排列 \(P\)，定义 \(F(P)\) 是满足 \(F(P)_x = [a_x = \max\limits_{i=1}^{x} a_i]\) 的 \(01\) 序列。

现在小 Oken 知道了 \(C = F(A)\)，她需要还原排列 \(A\)。

同时，小 Oken 还通过一些特殊手段掌握了 \(A\) 中一些下标对应的数值。

求出在所有 \(2^n\) 种情况中，小 Oken 能还原出的字典序最小的排列恰好是 \(A\) 的方案数。

答案对 \(998244353\) 取模。

\(1 \leq n \leq 10^6\)。

---

从小 Oken 的角度出发，考虑她在知道 \(C\) 后对 \(A\) 结构的洞察。

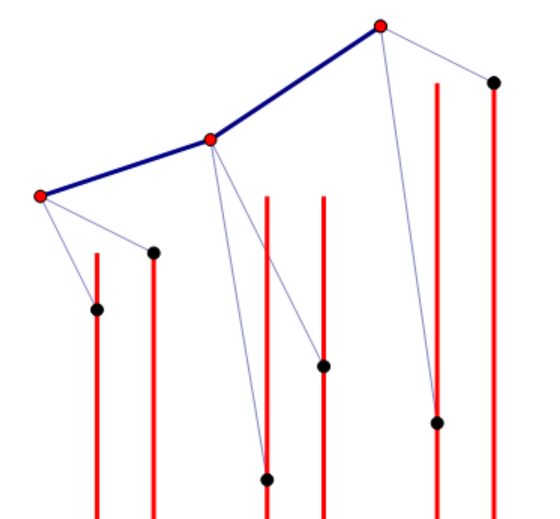
不妨假设小 Oken 已经通过神秘手段确定了所有红点的值，即所有前缀最大值。

此时我们发现，能还原出的字典序最小的排列恰好是 \(A\)，等价于没有确定的位置单调递增。

考虑下面的两个白点：

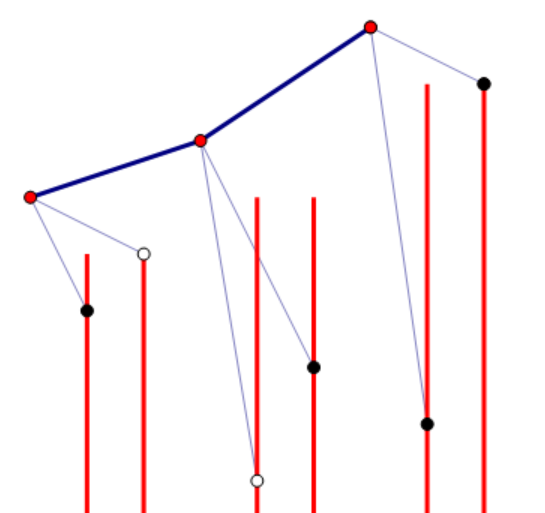
其中前面的值比后面的大，且这两个值都没有被确定。

显然，我们可以发现下面的情况也是合法的：

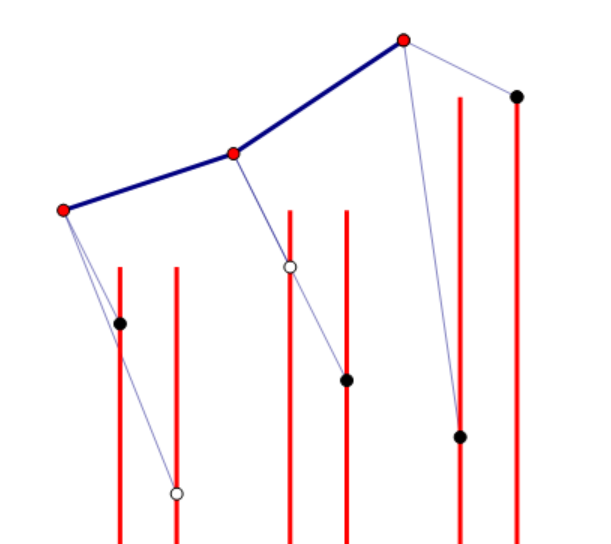
也就是说，对于所有没有确定的点，不可能出现前面的值比后面的大的情况。

我们也就说明了，没有确定值的点都是单调递增的。

通过这一点，我们就可以通过特殊性质 \(B\) 了。

你发现特殊性质 \(B\) 中只有第一个点是红点，显然这个问题等价于上升子序列计数。

---

你发现上面的这个东西在有红点没有确定时仍然成立。

首先我们需要保证，未选择的红点和黑点分别是单调递增的。

考虑什么样的情况不合法，发现能够交换一前一后的两个点，使得字典序变小。

对于一个未确定的前缀最大值 \(i\)，则不存在另一个未确定的位置 \(j\)，使得：

• \(i < j\)

• \(a_i > a_j\)

• 交换 \(i\) 和 \(j\) 后仍然满足条件

显然这是个充要条件，接下来就应该考虑计数了。

显然每个前缀最大值的未知性都是相互独立的，这点很重要。

不妨假设 \(i\) 后面的前缀最大值为 \(k\)，则 \(j\) 不能介于 \(a_1\) 到 \(a_{k-1}\) 的次大值和最大值之间。

假设我们确定了每个非前缀最大值的选择情况，则每个前缀最大值都会有 \(1\) 或 \(2\) 的系数。

对于所有非前缀最大值进行 dp 转移，可以做到 \(O(n^2)\)。

加个树状数组，变成 \(O(n \log n)\) 是容易的。

//Ad astra per aspera
#include<iostream>
#include<cstdio>
using namespace std;
const long long mod=998244353,inv2=499122177;
int n,a[1000010],pos[1000010],pos_maxn[1000010];
bool c[1000010];
int l[1000010],r[1000010],tot;
int cnt1[1000010],cnt2[1000010],vis[1000010];
const int V=1000000;
long long pow_2[1000010],invpow_2[1000010],dp[1000010];
void init(){
	pow_2[0]=invpow_2[0]=1;
	for(int i=1;i<=V;i++){
		pow_2[i]=pow_2[i-1]*2%mod;
		invpow_2[i]=invpow_2[i-1]*inv2%mod;
	}
}
long long fwk[1000010];
void modify(int pos,long long val){
	while(pos<=n){
		fwk[pos]+=val;
		fwk[pos]=(fwk[pos]%mod+mod)%mod;
		pos+=pos&-pos;
	}
}
long long query(int pos){
	long long ans=0;
	while(pos>=1){
		ans+=fwk[pos];
		ans=(ans%mod+mod)%mod;
		pos-=pos&-pos;
	}
	return ans;
}
int main(){
	init();
	int test_id,test_tot=1;
	scanf("%d",&test_id);
	while(test_tot--){
		int pre_maxn=0;
		scanf("%d",&n);
		tot=0;
		for(int i=1;i<=n;i++){
			fwk[i]=0;
			vis[i]=0;
			cnt1[i]=0;
			cnt2[i]=0;
			scanf("%d",&a[i]);
			pos[a[i]]=i;
			pre_maxn=max(pre_maxn,a[i]);
			if(pre_maxn==a[i]){
				pos_maxn[++tot]=i;
				c[i]=true;
			}
			else{
				c[i]=false;
			}
		}
		pos_maxn[tot+1]=n+1;
		for(int i=1;i<=tot;i++){
			int lst=a[pos_maxn[i-1]];
			for(int j=a[pos_maxn[i-1]]+1;j<=a[pos_maxn[i]]-1;j++){
				if(pos[j]<pos_maxn[i+1]){
					lst=j;
				}
			}
			l[i]=lst+1;
			r[i]=a[pos_maxn[i]]-1;
		}
		for(int i=1;i<=tot;i++){
			for(int j=l[i];j<=r[i];j++){
				vis[j]=i;
			}
			cnt1[l[i]]++;
			cnt2[r[i]+1]++;
		}
		for(int i=1;i<=n;i++){
			cnt1[i]+=cnt1[i-1];
			cnt2[i]+=cnt2[i-1];
		}
		dp[0]=1;
		modify(a[0]+1,dp[0]*invpow_2[cnt1[0]]%mod);
		for(int i=1;i<=n;i++){
			if(!c[i]){
				dp[i]=query(a[i])*pow_2[cnt2[a[i]]]%mod;
				modify(a[i]+1,dp[i]*invpow_2[cnt1[a[i]]]%mod);
				if(vis[a[i]]){
					modify(a[i]+1,dp[i]*invpow_2[cnt1[a[i]]]%mod);
					modify(r[vis[a[i]]]+1,-dp[i]*invpow_2[cnt1[a[i]]]%mod);
				}
			}
		}
		long long ans=0;
		for(int i=0;i<=n;i++){
			if(!c[i]){
				ans+=dp[i]*pow_2[tot-cnt1[a[i]]]%mod;
				ans=(ans%mod+mod)%mod;
			}
		}
		printf("%lld",ans);
	}
	return 0;
}