AGC020F Arcs on a Circle 题解

题目传送门：AGC020F Arcs on a Circle。

首先考虑断环为链，将最长弧的一端作为端点断开。

如果是实数，我们无法记录状态，我们发现由于每个弧长都是整数，相当于只需要考虑小数的相对顺序即可，相当于是对小数进行了离散化，那么题目转化为 \(nc-1\) 个整点的问题。

首先用 \((n-1)!\) 枚举相对顺序即全排列，那么第 \(i\) 个位置一定是编号为 \(i \bmod n\) 的弧，然后考虑 dp 表示前 \(i\) 个位置，能覆盖到 \(j\) 的位置且目前每个数的使用情况为 \(k\) 的方案数，转移的话直接考虑是否使用第 \(i\bmod n\) 条线段即可。

至于一开始为什么用最长弧，因为如果不使用最长弧，就可能会出现下面这种情况而不好处理，而选择最大值就不会这种情况。

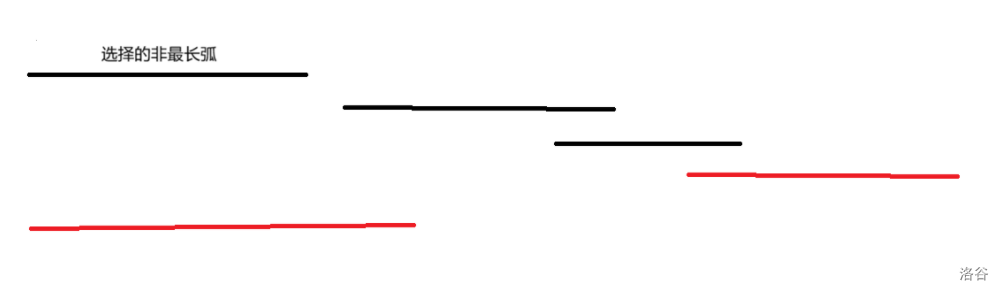
最后答案即为所有方案数加起来除上 \((n-1)!c^{n-1}\)。

#include<bits/stdc++.h>
#define int long long
#define double long double
using namespace std;
const int N=1<<7,M=310;
int f[M][M][N],n,c,a[M],p[N];
inline int read(){
	char c=getchar();
	int f=1,ans=0;
	while(c<48||c>57) f=(c==45?f=-1:1),c=getchar();
	while(c>=48&&c<=57) ans=(ans<<1)+(ans<<3)+(c^48),c=getchar();
	return ans*f;
}
inline int solve(){
	memset(f,0,sizeof(f));
	f[0][a[n]*n][0]=1;
	for (int i=1;i<=n*c;i++) for (int j=i;j<=n*c;j++){
		for (int k=0;k<(1<<n-1);k++) f[i][j][k]+=f[i-1][j][k];
		int x=i%n;
		if (x==0) continue;
		for (int k=0;k<(1<<n-1);k++) if ((k>>x-1)&1) f[i][min(n*c,max(j,i+a[p[x]]*n))][k]+=f[i-1][j][k^(1<<x-1)];
	}
	return f[n*c-1][n*c][(1<<n-1)-1];
}
main(){
	n=read(),c=read();
	for (int i=1;i<=n;i++) a[i]=read(),p[i]=i;
	sort(a+1,a+n+1);
	double ans=0;
	do{ans+=solve();}while(next_permutation(p+1,p+n));
	for (int i=1;i<n;i++) ans/=1.0*i*c;
	printf("%.15Lf",ans);
    return 0;
}