【信号处理】互相关，自相关

https://zhuanlan.zhihu.com/p/62292503
https://www.zhihu.com/question/22298352/answer/637156871

1.卷积

所得是关于n的函数（有些表达式中n写作τ，图中的τ写作t）

（1）概念

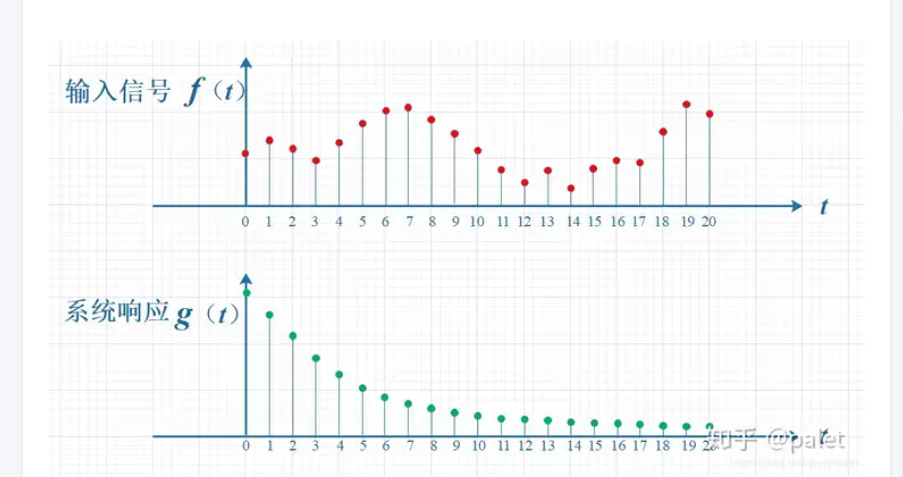
如下图所示，输入信号是 f(t) ，是随时间变化的。系统响应函数是 g(t) ，图中的响应函数是随时间指数下降的，它的物理意义是说：如果在 t=0 的时刻有一个输入，那么随着时间的流逝，这个输入将不断衰减。换言之，到了 t=T时刻，原来在 t=0 时刻的输入f(0)的值将衰减为f(0)g(T)。
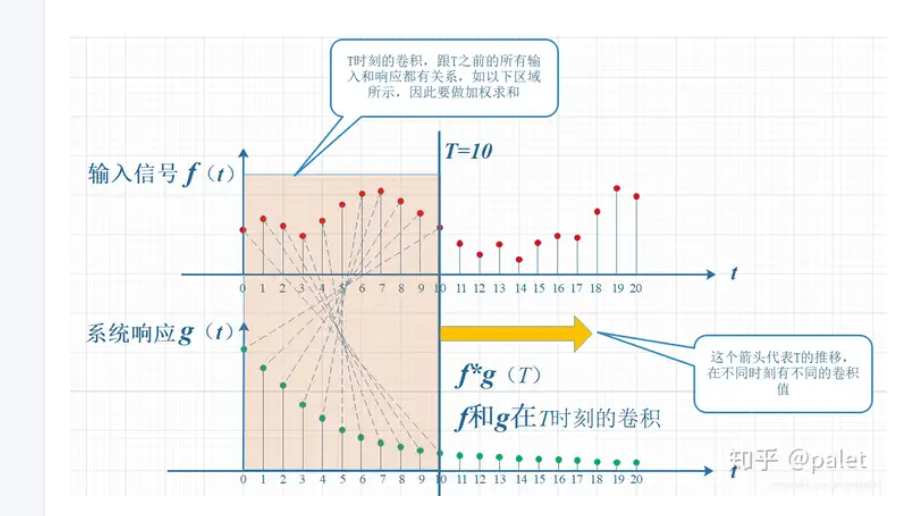
考虑到信号是连续输入的，也就是说，每个时刻都有新的信号进来，所以，最终输出的是所有之前输入信号的累积效果。如下图所示，在T=10时刻，输出结果跟图中带标记的区域整体有关。其中，f(10)因为是刚输入的，所以其输出结果应该是f(10)g(0)，而时刻t=9的输入f(9)，只经过了1个时间单位的衰减，所以产生的输出应该是 f(9)g(1)，如此类推，即图中虚线所描述的关系。这些对应点相乘然后累加，就是T=10时刻的输出信号值，这个结果也是f和g两个函数在T=10时刻的卷积值。

（2）总结

在机器学习和图像处理领域，卷积的主要功能是在一个图像(或某种特征)上滑动一个卷积核(即滤波器)，通过卷积操作得到一组新的特征。在计算卷积的过程中，需要进行卷积核翻转。在具体实现上，一般会以互相关操作来代替卷积，从而会减少一些不必要的操作或开销。互相关(Cross-Correlation)是一个衡量两个序列相关性的函数，通常是用滑动窗口的点积计算来实现。亦称为“不翻转的卷积”。

2.互相关

（1）概念

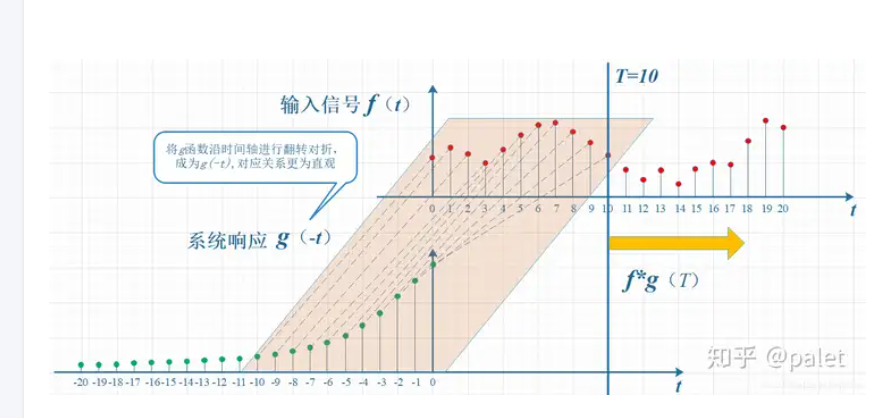
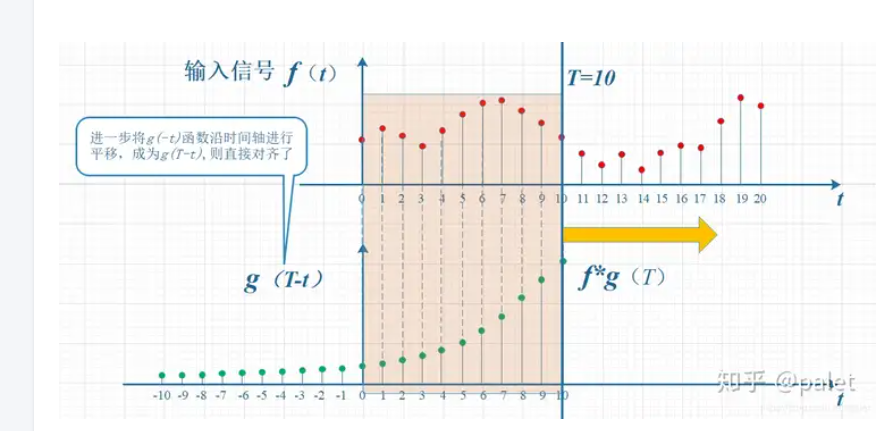
互相关函数和卷积运算类似，也是两个序列滑动相乘，但是区别在于：互相关的两个序列都不翻转，直接滑动相乘，求和；卷积的其中一个序列需要先翻转，然后滑动相乘，求和。所以，f(t)和g(t) 做相关等于 f*(-t) 与 g(t) 做卷积。但互相关和卷积在数学形式上的类似是一种巧合。
互相关的作用是为了找到信号在哪一时刻与另一信号最像（另一信号为本身时就是自相关），是用来表示两个信号之间相似性的一个度量。有时也称为滑动点积。
反映的是两个函数在不同的相对位置上互相匹配的程度。
互相关和自相关在本质上是两个函数做内积运算。即向量内积的连续形式。其在线性空间角度上的意义是：一个向量在另一个向量上的投影，内积结果越大，投影越大，两个向量间夹角越小，方向越一致，相似度越高。
两个信号（无论1维，2维还是n维）越相似，则重叠的面积越大，互相关就越大。

（2）计算方法

第一个函数右移，第二个函数保持不变。或，第二个函数左移，第一个函数保持不变。
效果一致，表现出来就是，第二个函数在第一个函数的左边。

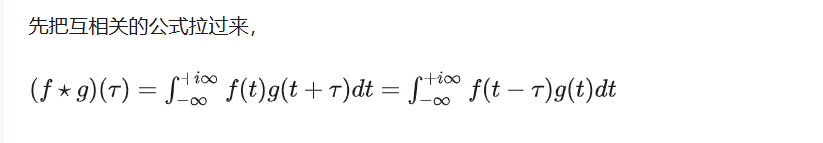
（3）性质

1.那么如果当某个信号延迟到一个值τ=T时，互相关出现了一个最大值，说明这个时候t=T时两个信号形状最接近。
2.由于时域上是卷积，所以互相关的傅里叶变换其实是两个信号各自傅里叶变换的乘积，这个性质就很有用。

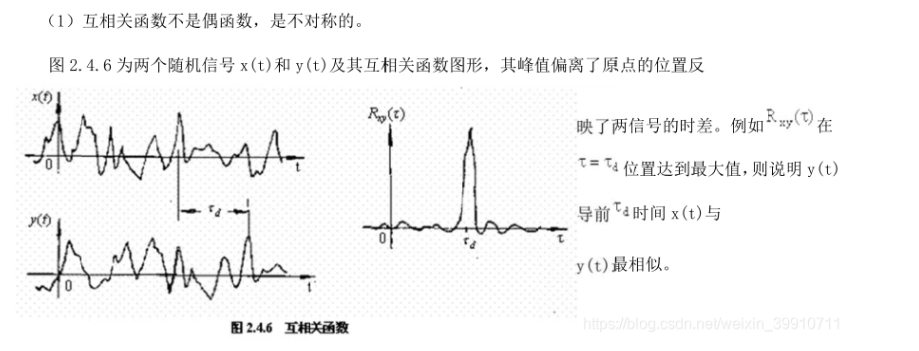
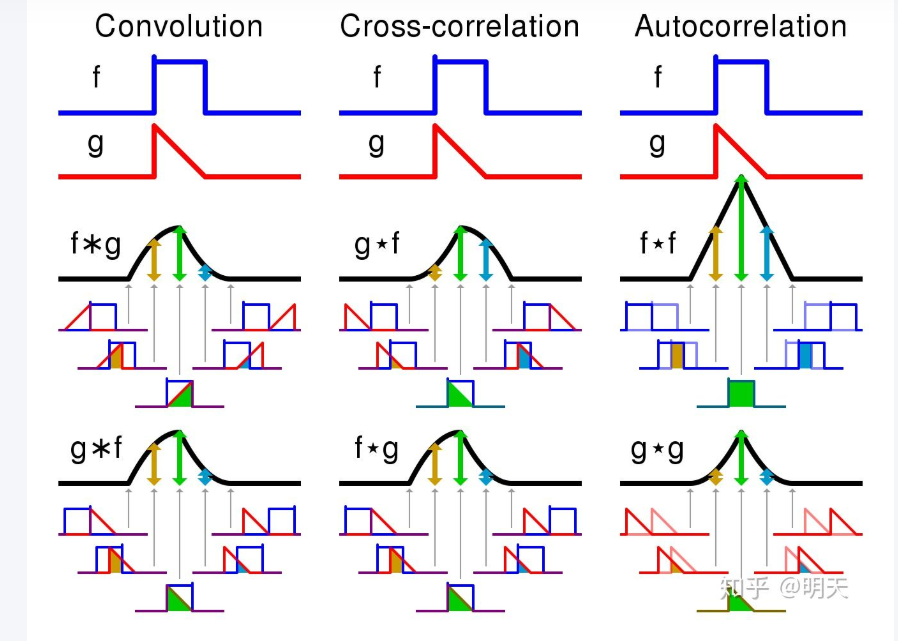
（4）总结

1.两个函数做相关运算，本质上是两个函数做内积运算。即向量内积的连续形式。
2.两个向量做内积的物理意义是:一个向量在另一个向量上的投影。
3.在内积空间的一组正交基下，内积结果越大，投影越大，两个向量间夹角越小，方向越致，相似度越高。
4。从向量可以推广到函数(连续时间信号)，离散相乘推广到连续积分。

3.自相关

（1）概念

自相关函数是描述随机信号 x(t) 在任意不同时刻 t1,t2的取值之间的相关程度。自相关函数，是对信号自身的互相关， 表示同一序列不同时刻的相关程度。是用寻找重复模式的数字工具，就如一个存在被覆盖噪声的周期信号，或识别丢失的基频。它经常被用于信号处理中的分析函数或序列，如时域信号。

我个人认为相似性可以理解成类似于可预测性(predictability)的意思。自相关在原点处总是取到峰值，而把一个函数平移一点点（对应 很小的情况），那么自相关函数取到接近峰值，说明这时候函数还是可预测的，你可以大致从相邻值推算出这个函数过了一小会产生什么结果，但是当自相关函数接近0的时候，说明远方的信号已经是你不能仅从 附近的观测进行预测的了。

什么情况下
很大的时候，自相关函数也能取到一个很大的值呢？

最简单的答案就是周期信号。当正好等于原来信号中的模式(pattern)重复的周期时，自相关函数会产生峰值 (如下图)。当函数具有周期性的时候，你显然也可以从一个周期内的观测值去预测远方的取值。因此，自相关函数经常被用作周期性分析。

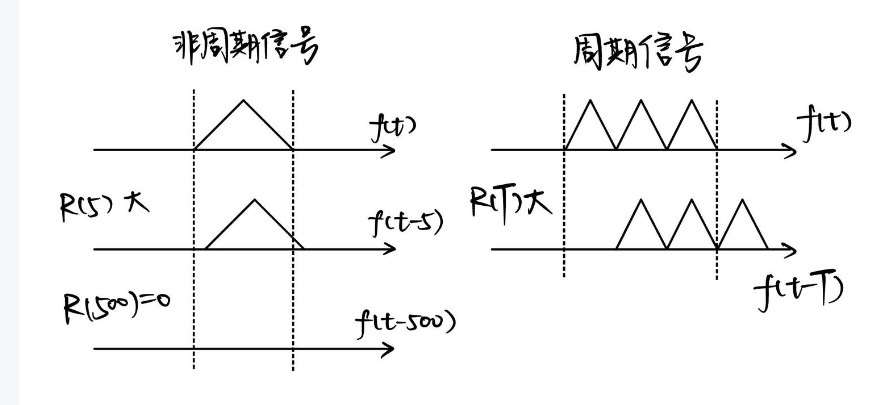
当然实际信号总是有限长的，所以自相关函数整体上是衰减的。

（2）性质

（3）计算方法

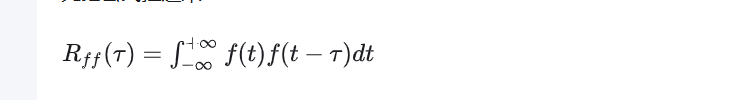
4. QA

互相关和卷积是同一个东西吗？

不要让求卷积和互相关的数学相似性迷惑你，它们描述了不同的信号处理过程。卷积是系统输入信号、输出信号和冲激响应之间的关系。互相关是一种在噪声背景下检测已知信号的方法。二者在数学上的相似仅仅是一种巧合。”实际上，只要注意到卷积操作是满足交换律的，而互相关操作并不满足交换律。仅此一点也许就能说明它们有着本质的不同吧。
————————————————

                        版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

原文链接：https://blog.csdn.net/weixin_39910711/article/details/112726698