字符串专题
前言
写题不过脑子的后果就是写完板子后一个月再回来就不会了
一.Manacher
马拉车可以在 \(O(n)\) 的时空复杂度内处理回文子串问题。
由于回文串根据长度分为“奇偶”两种,不好统一处理,所以其预处理时会在每个字符间插入一个特殊字符(比如 # $)
for (int i=1;i<=n;i++) s1+="$",s1+=s[i];
n=n*2; s=s1+"$";
for (int i=1;i<=n;i++)
{
if (i<=pr) p[i]=min(p[pos*2-i],pr-i);
while (i+p[i]<n&&i-p[i]>0&&s[i+p[i]+1]==s[i-p[i]-1]) p[i]++;
if (i+p[i]>pr) pr=i+p[i],pos=i;
}
其中 \(p_i\) 记录的是以 \(s_i\) 为回文中心时的最长回文半径。其正确性与复杂度分析有点像 Z 函数
正确性&时间复杂度
在当前处理过的所有回文串中,设右端点最靠右的回文子串的回文中心为 \(pos\),其最长回文子串右端点为 \(pr=pos+p_{pos}\),当前要处理 \(p_i\)
画工不精,就不放图了……
若 \(i\in[pos,pr]\),那么显然它与 \(pos\times 2-i\) 对称,且在大回文串的范围内以 \(pos\times 2-i\) 为回文中心的回文串和以 \(i\) 为回文中心的相同。so 可以先将其赋值为 \(pos\times 2-i\) 在大回文串中的回文半径,再暴力拓展。
此处的“暴力拓展”有个 while,不好直接瞪出复杂度,但其与 Z 函数的复杂度分析是一样的。当 \(p_i\) 取的是 \(p_{pos\times 2-i}\) 时,因为在大回文串内它都无法继续匹配了所以此时 \(p_i\) 不会再继续拓展;反之,\(p_i\) 取到 \(pr-i\) 时再拓展一定会使得 \(pr\) 指针右移,指针的右移次数上限为 \(O(n)\) 所以总复杂度也是 \(O(n)\)
P1872 回文串计数
我刚开始非常唐地以为这是一个三维数点,直到看到题解……
刚开始跑出来所有回文中心的最长回文串。完全不用三维数点啊,只需要记录一个 \(pre_i\) 记录以 \(i\) 开头的回文串个数,\(lst_i\) 记录以 \(i\) 结尾的回文串个数,那么最终答案就是
因为在最后统计一下答案就行,所以这在求得每个回文串后给首尾差分一下即可。不需要任何数据结构
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
string s,s1;
int n,p[N],pr,pos;
int pre[N],lst[N],ans;
signed main()
{
cin>>s; n=s.size(),s=" "+s;
for (int i=1;i<=n;i++) s1+="$",s1+=s[i];
n=n*2; s=s1+"$"; pos=pr=ans=0;
for (int i=1;i<=n;i++)
{
if (i<=pr) p[i]=min(p[pos*2-i],pr-i);
while (i+p[i]<n&&i-p[i]>0&&s[i+p[i]+1]==s[i-p[i]-1]) p[i]++;
if (i+p[i]>pr) pr=i+p[i],pos=i;
if (p[i]==0&&i%2==0) continue;
if (i%2==0) pre[i/2+1-p[i]/2]++,pre[i/2+1]--,lst[i/2+1]++,lst[i/2+p[i]/2+1]--;
else pre[i/2+1-p[i]/2]++,pre[i/2+2]--,lst[i/2+1]++,lst[i/2+2+p[i]/2]--;
}
for (int i=1;i<=n/2;i++) pre[i]+=pre[i-1],lst[i]+=lst[i-1];
for (int i=1;i<=n/2;i++) { ans+=pre[i]*lst[i-1]; lst[i]+=lst[i-1]; }
cout<<ans<<"\n"; return 0;
}
P4555 [国家集训队] 最长双回文串
考虑记 \(f_i\) 表示以 \(i\) 结尾的最长回文串长度,计算答案只需正反跑两遍。手模后容易发现,一个 \(f_i\) 会在距离其最远的回文中心处被更新,也就是说对于一个回文串只需用其更新被它覆盖范围内尚且没值的位置,容易发现这样的位置一定会是这个回文串的后缀。这样的话均摊下来就是 \(O(n)\) 的,可以过
代码
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+3;
string s,s1;
int n,f1[100002],f2[100002],ans;
int p[N],pos,pr;
void manacher(string s,int *f)
{
pos=0,pr=0;
for (int i=0;s[i]!='\0';i++)
{
if (i<=pr) p[i]=min(pr-i,p[(pos<<1)-i]);
else p[i]=0;
while (s[i+p[i]+1]!='\0'&&s[i+p[i]+1]==s[i-p[i]-1]) p[i]++;
if (i+p[i]>pr)
{
pos=i; pr=i+p[i];
int now=(pr+1)>>1,len=((p[i]>>1)<<1)+(i&1),ea=(i>>1)+1;
while (now>=ea&&!f[now]) { f[now]=len; len-=2; now--; }
}
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>s; n=s.size();
for (int i=0;s[i]!='\0';i++) s1+="$",s1+=s[i];
s=s1+"$"; manacher(s,f1);
reverse(s.begin(),s.end()),manacher(s,f2);
for (int i=2;i<n;i++) ans=max(ans,f1[i]+f2[n-i]);
cout<<ans; return 0;
}
金牌导航·Manacher 字符串连接
容易发现对于以 \(i\) 为回文中心的每个回文串只有最长的那个回文串才可能起作用。
接着可能有一个朴素的想法,设 \(f_i\) 表示拼接前缀 \([1,i]\) 所需的最少回文串个数。显然 \(f_i\) 具有单调性,所以每个长回文串 \([l,r]\) 的贡献就是 \(f_r\leftarrow min_{i=l-1}^{mid}(f_i)+1\),其中 \(mid\) 指该串的回文中心。在马拉车的过程中,若当前串的右端点未超过当前的右端点,那么这个串肯定是被包含的,即无用的。所以只有在移动右指针时再更新就可以了
其实这道题也可以将所有更新了右指针的长回文串存下来然后转换成区间覆盖问题。但我还是选择我的无脑做法
代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+3;
const int inf=0x3f3f3f3f;
string s,s1;
int n,p[N];
struct Segment_Tree
{
struct node{
int l,r;
int mn;
}tr[N<<2];
void push_up(int id) { tr[id].mn=min(tr[id<<1].mn,tr[id<<1|1].mn); }
void build(int id,int l,int r)
{
tr[id].l=l,tr[id].r=r; tr[id].mn=inf;
if (l==r) return ;
int mid=(l+r)>>1;
build(id<<1,l,mid),build(id<<1|1,mid+1,r);
}
void update(int id,int pos,int k)
{
if (tr[id].l==tr[id].r&&tr[id].l==pos) { tr[id].mn=k; return ; }
int mid=(tr[id].l+tr[id].r)>>1;
if (mid>=pos) update(id<<1,pos,k);
else update(id<<1|1,pos,k); push_up(id);
}
int query(int id,int l,int r)
{
if (tr[id].l>=l&&tr[id].r<=r) return tr[id].mn;
int mid=(tr[id].l+tr[id].r)>>1,res=inf;
if (mid>=l) res=min(res,query(id<<1,l,r));
if (mid+1<=r) res=min(res,query(id<<1|1,l,r));
return res;
}
}Tr;
void solve()
{
s1=""; n=s.size();
for (int i=0;s[i]!='\0';i++) s1+="$",s1+=s[i];
s=s1+"$"; Tr.build(1,0,n); Tr.update(1,0,0);
int pr=0,pos=0;
for (int i=0;s[i]!='\0';i++)
{
p[i]=(i<=pr?min(p[pos*2-i],pr-i):0);
while (i-p[i]-1>=0&&s[i+p[i]+1]==s[i-p[i]-1]) p[i]++;
if (i+p[i]>pr)
{
pr=i+p[i]; pos=i;
if (!p[i]&&i%2==0) continue;
Tr.update(1,(i+p[i])/2,Tr.query(1,(i-p[i])/2,(i+p[i])/2)+1);
}
}
cout<<Tr.query(1,n,n)-1<<"\n";
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
while (cin>>s) solve(); return 0;
}
金牌导航·Manacher 有趣回文串
考虑记 \(f1_i\) 表示以 \(i\) 结尾的回文串的左端点之和,记 \(f2_i\) 表示以 \(i\) 开头的回文串的右端点之和,那么最后的答案形式就是 \(\sum{f1_i\times f2_{i+1}}\)
考虑以 \(i\) 为回文中心的回文串的贡献。有一个想法是线段树差分直接求,亲测卡不过。考虑对于第 \(i\) 位其会被贡献 \(mid\times 2-i\),然后差分一下每个 \(i\) 的出现次数和 \(2\times\sum{mid}\) 即可
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+5;
const int MOD=1e9+7;
string s,s1;
int n,f1[N],f2[N],ans;
int p[N<<1],pr,pos;
int d1[N],d2[N],D1[N],D2[N];
void manacher()
{
pr=pos=0;
for (int i=0;s[i]!='\0';i++)
{
p[i]=(i<=pr?min(pr-i,p[pos*2-i]):0);
while (i-p[i]-1>=0&&s[i+p[i]+1]==s[i-p[i]-1]) p[i]++;
if (p[i]+i>pr) pr=i+p[i],pos=i;
d2[i/2+i%2]++,d2[(i-p[i])/2]--;
d1[i/2+i%2]+=i+1,d1[(i-p[i])/2]-=i+1;
D2[(i+p[i])/2]++,D2[i/2]--;
D1[(i+p[i])/2]+=i+1,D1[i/2]-=i+1;
}
d1[n+1]=d2[n+1]=0; D1[n+1]=D2[n+1]=0;
for (int i=n;i>=1;i--) d2[i]+=d2[i+1],d1[i]+=d1[i+1],f2[i]=(d1[i]-d2[i]*i)%MOD;
for (int i=n;i>=1;i--) D2[i]+=D2[i+1],D1[i]+=D1[i+1],f1[i]=(D1[i]-i*D2[i])%MOD;
for (int i=0;i<=n+2;i++) d1[i]=d2[i]=D1[i]=D2[i]=0;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
while (cin>>s)
{
s1="",n=s.size();
for (int i=0;s[i]!='\0';i++) s1+="$",s1+=s[i];
s=s1+"$"; manacher(); ans=0;
for (int i=1;i<n;i++) ans=(ans+f1[i]*f2[i+1]%MOD)%MOD;
cout<<ans<<"\n";
}
return 0;
}
二.后缀数组 SA
1.\(sa_i\) 与 \(rk_i\)
有一下标为 \([1,|s|]\) 的字符串 \(s\),对其所有后缀进行排序,令 \(sa_i\) 为第 \(i\) 小的后缀的起始下标,\(rk_i\) 为后缀 \(s[i...n]\) 的排名。字符串的比较是 \(O(|S|)\) 的,若是直接 sort 排序复杂度会达到 \(O(n^2\log n)\),所以一般是用基数排序+倍增做到 \(O(n \log n)\)
void qsort()
{
//此处相当于以上一轮的 rk 为第一关键字,tmp 为第二关键字升序排序
for (int i=0;i<=m;i++) sum[i]=0;
for (int i=1;i<=n;i++) sum[rk[i]]++;
for (int i=1;i<=m;i++) sum[i]+=sum[i-1];
for (int i=n;i>=1;i--) sa[sum[rk[tmp[i]]]--]=tmp[i];
}
void build()
{
for (int i=1;i<=n;i++) rk[i]=s[i],tmp[i]=i;
qsort();
for (int w=1,tol=0;tol<n;m=tol,w<<=1)
{
//tol 是排名的数量,w 是倍增的第二关键字前缀长度
//倍增时是以每个前缀的前 w/2 部分的排名为第一关键字、后 w/2 的排名以第二关键字进行排序
//因为倍增,所以前后两半的排名都已知
tol=0;
for (int i=n-w+1;i<=n;i++) tmp[++tol]=i;//这些前缀长度不足 w,按照空串处理
for (int i=1;i<=n;i++) if (sa[i]>w) tmp[++tol]=sa[i]-w;//在 w 的倍增意义下,上一轮的sa[i] 实际对应的是这一轮的 sa[i]-w 的后半截
qsort(),swap(rk,tmp);
//因为可能会出现rk相同的情况,所以不能直接 rk[sa[i]]=i 此时的 tmp 其实是上一轮的 rk
tol=rk[sa[1]]=1;=i
for (int i=2;i<=n;i++) rk[sa[i]]=(tmp[sa[i]]==tmp[sa[i-1]]&&tmp[sa[i]+w]==tmp[sa[i-1]+w]?tol:++tol);
}
}
2.\(ht_i\)
对于排序后的所有后缀,记 \(ht_i\) 表示第 \(i-1\) 小的后缀与第 \(i\) 小的后缀的 LCP(最长公共前缀)长度。有引理
\(ht_{rk_i}\geqslant ht_{rk_{i-1}}-1\)
证明待补。所以可以 \(O(n)\) 得到 \(ht\) 数组
inline void get_ht()
{
for (int i=1;i<=n;i++)
{
if (!rk[i]) continue;
ht[rk[i]]=ht[rk[i-1]];
if (ht[rk[i]]) ht[rk[i]]--;
while (s[i+ht[rk[i]]]==s[sa[rk[i]-1]+ht[rk[i]]]) ht[rk[i]]++;
}
}
显然,后缀 \(sa_i,sa_j(i<j)\) 的 LCP 长度为 \(min_{k=i+1}^j \{ht_k\}\),可以用 ST 表维护区间最小值 \(O(1)\) 求得后缀 LCP
结构体封装完整代码
struct SA
{
int sa[N],rk[N],ht[N];
int sum[N],tmp[N];
int st[N][20],lg[N];
void qsort()
{
for (int i=0;i<=m;i++) sum[i]=0;
for (int i=1;i<=n;i++) sum[rk[i]]++;
for (int i=1;i<=m;i++) sum[i]+=sum[i-1];
for (int i=n;i>=1;i--) sa[sum[rk[tmp[i]]]--]=tmp[i];
}
void build()
{
for (int i=1;i<=n;i++) rk[i]=s[i],tmp[i]=i;
qsort();
for (int w=1,tol=0;tol<n;m=tol,w<<=1)
{
tol=0;
for (int i=n-w+1;i<=n;i++) tmp[++tol]=i;
for (int i=1;i<=n;i++) if (sa[i]>w) tmp[++tol]=sa[i]-w;
qsort(),swap(rk,tmp);
tol=rk[sa[1]]=1;
for (int i=2;i<=n;i++) rk[sa[i]]=(tmp[sa[i]]==tmp[sa[i-1]]&&tmp[sa[i]+w]==tmp[sa[i-1]+w]?tol:++tol);
}
}
void get_ht()
{
for (int i=1;i<=n;i++)
{
if (!rk[i]) continue;
ht[rk[i]]=ht[rk[i-1]];
if (ht[rk[i]]) ht[rk[i]]--;
while (s[i+ht[rk[i]]]==s[sa[rk[i]-1]+ht[rk[i]]]&&s[i+ht[rk[i]]]!='$') ht[rk[i]]++;
}
lg[0]=-1; for (int i=1;i<=n;i++) lg[i]=lg[i>>1]+1;
for (int i=1;i<=n;i++) st[i][0]=ht[i];
for (int j=1;j<=lg[n];j++)
for (int i=1;i+(1<<j)-1<=n;i++) st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}
int mn(int l,int r)
{
int k=lg[r-l+1];
return min(st[l][k],st[r-(1<<k)+1][k]);
}
}sa;
P7409 SvT
看到“后缀”和“LCP”应该会先想到 SA 吧。
对于给出的 \(t\) 个后缀 \(i\),每次询问要求的相当于
看到这个式子大概就会想到计算每个 \(ht_i\) 的贡献次数吧。先通过 ST 表求出给出后缀排序后两两之间的 LCP 长度形成新的 \(ht\) 数组,再用单调栈分别搞一下 \(ht_i\) 左右第一个比它小的位置(注意去重)。记 \(f1_i\) 表示 \(i\) 后第一个小于等于 \(ht_i\) 的位置,\(f2_i\) 为 \(i\) 前第一个小于 \(ht_i\) 的位置,最终答案就是
复杂度在于初始化 SA 和给定后缀排序的 \(O(n\log n)\)
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e5+5;
const int M=3e6+5;
int n,q,m=200;
int t,a[N],tmp[N];
int st[M],tl,f1[M],f2[M],ans;
string s;
struct SA
{
int sa[N],rk[N],ht[N];
int sum[N],tmp[N];
int st[N][22],lg[N];
inline void qsort()
{
for (int i=0;i<=m;i++) sum[i]=0;
for (int i=1;i<=n;i++) sum[rk[i]]++;
for (int i=1;i<=m;i++) sum[i]+=sum[i-1];
for (int i=n;i>=1;i--) sa[sum[rk[tmp[i]]]--]=tmp[i];
}
inline void build()
{
for (int i=1;i<=n;i++) rk[i]=s[i],tmp[i]=i;
qsort();
for (int w=1,tol=0;tol<n;m=tol,w<<=1)
{
tol=0;
for (int i=n-w+1;i<=n;i++) tmp[++tol]=i;
for (int i=1;i<=n;i++) if (sa[i]>w) tmp[++tol]=sa[i]-w;
qsort(),swap(rk,tmp);
tol=rk[sa[1]]=1;
for (int i=2;i<=n;i++) rk[sa[i]]=(tmp[sa[i]]==tmp[sa[i-1]]&&tmp[sa[i]+w]==tmp[sa[i-1]+w]?tol:++tol);
}
}
inline void get_ht()
{
for (int i=1;i<=n;i++)
{
if (!rk[i]) continue;
ht[rk[i]]=ht[rk[i-1]];
if (ht[rk[i]]) ht[rk[i]]--;
while (s[i+ht[rk[i]]]==s[sa[rk[i]-1]+ht[rk[i]]]) ht[rk[i]]++;
}
lg[0]=-1;
for (int i=1;i<=n;i++) lg[i]=lg[i>>1]+1;
for (int i=1;i<=n;i++) st[i][0]=ht[i];
for (int j=1;j<=lg[n];j++)
for (int i=1;i+(1<<j)-1<=n;i++) st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}
int get_mn(int l,int r) { int k=lg[r-l+1]; return min(st[l][k],st[r-(1<<k)+1][k]); }
}sa;
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>q>>s; s=" "+s;
sa.build(),sa.get_ht();
while (q--)
{
cin>>t; ans=0;
for (int i=1;i<=t;i++) { cin>>a[i]; a[i]=sa.rk[a[i]]; }
sort(a+1,a+1+t); t=unique(a+1,a+1+t)-a-1;
for (int i=2;i<=t;i++) tmp[i]=sa.get_mn(a[i-1]+1,a[i]);
for (int i=2;i<=t;i++)
{
while (tl&&tmp[st[tl]]>=tmp[i]) { f1[st[tl]]=i; tl--; }
st[++tl]=i;
}
while (tl) { f1[st[tl]]=t+1; tl--; }
for (int i=t;i>=2;i--)
{
while (tl&&tmp[st[tl]]>tmp[i]) { f2[st[tl]]=i; tl--; }
st[++tl]=i;
}
while (tl) { f2[st[tl]]=1; tl--; }
for (int i=2;i<=t;i++) ans+=(i-f2[i])*(f1[i]-i)*tmp[i];
cout<<ans<<"\n";
}
return 0;
}
金牌导航·后缀数组 E.可重叠子串
考虑一些相似的后缀的前缀在 SA 中应该是连续的,所以直接在 \(ht\) 数组中滑动窗口就行
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e4+5;
int n,k,a[N],ans;
struct SA
{
int sa[N],rk[N],ht[N],m=N;
int sum[N],tmp[N];
int lg[N],st[N][16];
void qsort()
{
for (int i=0;i<=m;i++) sum[i]=0;
for (int i=1;i<=n;i++) sum[rk[i]]++;
for (int i=1;i<=m;i++) sum[i]+=sum[i-1];
for (int i=n;i>=1;i--) sa[sum[rk[tmp[i]]]--]=tmp[i];
}
void build()
{
for (int i=1;i<=n;i++) rk[i]=a[i],tmp[i]=i;
qsort();
for (int w=1,tol=0;tol<n;m=tol,w<<=1)
{
tol=0;
for (int i=n-w+1;i<=n;i++) tmp[++tol]=i;
for (int i=1;i<=n;i++) if (sa[i]>w) tmp[++tol]=sa[i]-w;
qsort(),swap(rk,tmp); tol=rk[sa[1]]=1;
for (int i=2;i<=n;i++) rk[sa[i]]=(tmp[sa[i]]==tmp[sa[i-1]]&&tmp[sa[i]+w]==tmp[sa[i-1]+w]?tol:++tol);
}
}
void get_ht()
{
for (int i=1;i<=n;i++)
{
if (!rk[i]) continue;
ht[rk[i]]=ht[rk[i-1]];
if (ht[rk[i]]) ht[rk[i]]--;
while (a[i+ht[rk[i]]]==a[sa[rk[i]-1]+ht[rk[i]]]) ht[rk[i]]++;
}
lg[0]=-1; for (int i=1;i<=n;i++) lg[i]=lg[i>>1]+1;
for (int i=1;i<=n;i++) st[i][0]=ht[i];
for (int j=1;j<=lg[n];j++)
for (int i=1;i+(1<<j)-1<=n;i++) st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}
int get_mn(int l,int r) { int k=lg[r-l+1]; return min(st[l][k],st[r-(1<<k)+1][k]); }
int get_ans()
{
int res=0;
for (int i=1;i+k-1<=n;i++) res=max(res,get_mn(i+1,i+k-1));
return res;
}
}sa;
void init()
{
int tmp[N],cnt;
for (int i=1;i<=n;i++) tmp[i]=a[i];
sort(tmp+1,tmp+1+n);
cnt=unique(tmp+1,tmp+1+n)-tmp-1;
for (int i=1;i<=n;i++) a[i]=lower_bound(tmp+1,tmp+1+cnt,a[i])-tmp;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>k;
for (int i=1;i<=n;i++) cin>>a[i];
init(); sa.build(),sa.get_ht();
cout<<sa.get_ans(); return 0;
}
金牌导航·后缀数组 公共串计数
仍是讨论每个 \(ht_i\) 的贡献,先试用单调栈搞出每个 \(ht_i\) 的贡献区间,因为这题要求的是俩串的子串,所以要分别计算左右端点处于两个子串的数量。注意一些加一减一的细节以及这题的勾史输入便好
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+10;
int k,n,n1;
char c[N],c1[N];
string s,s1;
struct SA
{
int sa[N],rk[N],ht[N];
int sum[N],tmp[N],m=200;
int f1[N],f2[N],st[N],tl;
int p1[N],p2[N];
void init()
{
m=200; tl=0;
memset(sa,0,sizeof sa);
memset(rk,0,sizeof rk);
memset(ht,0,sizeof ht);
memset(sum,0,sizeof sum);
memset(tmp,0,sizeof tmp);
memset(f1,0,sizeof f1);
memset(f2,0,sizeof f2);
memset(st,0,sizeof st);
memset(p1,0,sizeof p1);
memset(p2,0,sizeof p2);
}
void qsort()
{
for (int i=0;i<=m;i++) sum[i]=0;
for (int i=1;i<=n;i++) sum[rk[i]]++;
for (int i=1;i<=m;i++) sum[i]+=sum[i-1];
for (int i=n;i>=1;i--) sa[sum[rk[tmp[i]]]--]=tmp[i];
}
void build()
{
for (int i=1;i<=n;i++) rk[i]=s[i],tmp[i]=i;
qsort();
for (int tol=0,w=1;tol<n;m=tol,w<<=1)
{
tol=0;
for (int i=n-w+1;i<=n;i++) tmp[++tol]=i;
for (int i=1;i<=n;i++) if (sa[i]>w) tmp[++tol]=sa[i]-w;
qsort(),swap(rk,tmp); rk[sa[1]]=tol=1;
for (int i=2;i<=n;i++) rk[sa[i]]=(tmp[sa[i]]==tmp[sa[i-1]]&&tmp[sa[i]+w]==tmp[sa[i-1]+w]?tol:++tol);
}
for (int i=2;i<=n;i++)
{
f1[i]=f1[i-1],f2[i]=f2[i-1];
if (sa[i]>n1) f2[i]++; else f1[i]++;
}
f1[n+1]=f1[n],f2[n+1]=f2[n];
}
void get_ht()
{
for (int i=1;i<=n;i++)
{
if (!rk[i]) continue;
ht[rk[i]]=ht[rk[i-1]];
if (ht[rk[i]]) ht[rk[i]]--;
while (s[i+ht[rk[i]]]==s[sa[rk[i]-1]+ht[rk[i]]]&&s[i+ht[rk[i]]]!='$') ht[rk[i]]++;
}
}
int get_ans()
{
tl=0; int res=0;
for (int i=2;i<=n;i++)
{
while (tl&&ht[i]<ht[st[tl]]) p1[st[tl--]]=i;
st[++tl]=i;
}
while (tl) p1[st[tl--]]=n+1;
for (int i=n;i>=2;i--)
{
while (tl&&ht[i]<=ht[st[tl]]) p2[st[tl--]]=i;
st[++tl]=i;
}
while (tl) p2[st[tl--]]=1;
for (int i=2;i<=n;i++)
{
ht[i]=max(ht[i],k-1);
res+=(ht[i]-k+1)*((f2[p1[i]-1]-f2[i-1])*(f1[i-1]-f1[p2[i]-1])+(f1[p1[i]-1]-f1[i-1])*(f2[i-1]-f2[p2[i]-1]));
}
return res;
}
}sa;
void solve()
{
cin>>(c+1)>>(c1+1);
s=" ";
for (int i=1;c[i]!='\0';i++) s+=c[i];
n1=s.size()-1; s+="$";
for (int i=1;c1[i]!='\0';i++) s+=c1[i];
n=s.size()-1;
sa.init(); sa.build(); sa.get_ht();
cout<<sa.get_ans()<<"\n";
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
while (cin>>k) if (k) solve(); else return 0;
}
UVA11107 Life Forms
直接在 \(ht\) 数组上滑动窗口,然后用类似 P1381 单词背诵 的方式维护一个属于串串的数量大于 \(\lfloor \frac{n}{2}\rfloor\) 的窗口再 RMQ 出其 LCS 长度,其中的最大值就是答案长度。
但这输出是真恶心,有一种输出方法是得到 \(len\) 后将 \(ht\) 数组分为内部都大于等于 \(len\) 的若干段,然后判断串串数量是否大于 \(\lfloor \frac{n}{2}\rfloor\) 输出;还有一种方法是在找 \(len\) 的过程中将 LCS 长度为 \(len\) 的位置都放到 vector 中,手模后容易发现若此次 LCS 长度与上次 LCS 长度相同,那么它们对应的子串一定相同,即此时不能插入重复的答案。于是记录下上次的 LCS 长度 \(pre\) 再特判一下即可
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+110;
int k,n; string s1,s;
int f[N];
vector <int> ans;
struct sa
{
int sa[N],rk[N],ht[N];
int sum[N],tmp[N],m;
int st[N][20],lg[N];
void qsort()
{
for (int i=0;i<=m;i++) sum[i]=0;
for (int i=1;i<=n;i++) sum[rk[i]]++;
for (int i=1;i<=m;i++) sum[i]+=sum[i-1];
for (int i=n;i>=1;i--) sa[sum[rk[tmp[i]]]--]=tmp[i];
}
void build()
{
for (int i=1;i<=n;i++) rk[i]=s[i],tmp[i]=i;
m=200,qsort();
for (int w=1,tol=0;tol<n;m=tol,w<<=1)
{
tol=0;
for (int i=n-w+1;i<=n;i++) tmp[++tol]=i;
for (int i=1;i<=n;i++) if (sa[i]>w) tmp[++tol]=sa[i]-w;
qsort(); swap(rk,tmp);
rk[sa[1]]=tol=1;
for (int i=2;i<=n;i++) rk[sa[i]]=(tmp[sa[i]]==tmp[sa[i-1]]&&tmp[sa[i]+w]==tmp[sa[i-1]+w]?tol:++tol);
}
}
void get_ht()
{
for (int i=1;i<=n;i++)
{
if (!rk[i]) continue;
ht[rk[i]]=ht[rk[i-1]];
if (ht[rk[i]]) ht[rk[i]]--;
while (s[i+ht[rk[i]]]==s[sa[rk[i]-1]+ht[rk[i]]]&&s[i+ht[rk[i]]]!='$') ht[rk[i]]++;
}
lg[0]=-1; for (int i=1;i<=n;i++) lg[i]=lg[i>>1]+1;
for (int i=1;i<=n;i++) st[i][0]=ht[i];
for (int j=1;j<=lg[n];j++)
for (int i=1;i+(1<<j)-1<=n;i++) st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}
int q[N],hd,tl;
int get_mn(int l,int r) { int k=lg[r-l+1]; return min(st[l][k],st[r-(1<<k)+1][k]); }
int get_sum()
{
memset(sum,0,sizeof sum); ans.clear();
int tol=0,cnt=k/2+1,res=-1,pre=-1;
hd=1,tl=0;
for (int i=1;i<=n;i++)
{
q[++tl]=i; sum[f[sa[i]]]++;
if (sum[f[sa[i]]]==1) tol++;
while (hd<=tl&&(f[sa[q[hd]]]==0||tol>cnt||(tol==cnt&&sum[f[sa[q[hd]]]]!=1)))
{
sum[f[sa[q[hd]]]]--; if (!sum[f[sa[q[hd]]]]) tol--;
hd++;
}
if (tol>=cnt)
{
int ea=get_mn(q[hd]+1,q[tl]);
if (ea>res) { res=ea; ans.clear(); ans.push_back(sa[i]); }
else if (ea==res&&ea!=pre) ans.push_back(sa[i]);
pre=ea;
}
}
return res;
}
}sa;
void solve()
{
s="";
for (int i=1;i<=k;i++) { cin>>s1; s+="$",s+=s1; }
n=s.size()-1; int cnt=1; memset(f,0,sizeof f);
for (int i=1;i<=n;i++) if (s[i]=='$') cnt++; else f[i]=cnt;
sa.build(),sa.get_ht();
int len=sa.get_sum(),_size=ans.size();
if (!len) cout<<"?\n";
else for (int i=0;i<_size;i++) cout<<s.substr(ans[i],len)<<"\n";
cout<<"\n";
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
while (cin>>k) if (k) solve(); else return 0;
}
三.后缀自动机 SAM
SAM 学习笔记 然而写金牌导航还需要广义 SAM 的知识
CF700E Cool Slogans
首先容易发现,一定存在一种最优解使得 \(s_{i-1}\) 是 \(s_i\) 的 border,但在这道题中 \(s_{i-1}\) 与 \(s_i\) 的后缀关系更加重要,border 关系在这道题里没啥用
先根据串建出 SAM,因为前后的后缀关系,可以发现 \(s_{i-1}\) 代表的节点一定是 \(s_{i}\) 节点的祖先,所以考虑在 \(parent\) 树上 DP,由父节点向子节点转移。设 \(f_i\) 为考虑从根到 \(i\) 节点的最长序列长度。若 \(f_i\) 能从 \(f_{fa_i}\) 转移而来,根据“能选就选”原则,有 \(f_{i}=f_{fa_i}+1\),否则 \(f_{i}=f_{fa_i}\)。
首先,因为一个节点内串的 \(endpos\) 集合相同,转移只关注其出现位置,所以每个点都取其最长的串不会使得结果更劣。下文中的 \(len_i\) 指 \(i\) 节点的最长串长度。
现在考虑转移条件。对于节点 \(i\) 的串的一个结尾位置 \(p\),若在上一个转移节点的 \(endpos\) 集合中 \(p\) 的前驱 \(q\) 满足包含关系
即 \(endpos\) 集合中存在元素 \(q\) 满足
此时串 \(s[q-len_{q}+1,q]\) 在 \(s[p-len_p+1,p]\) 出现了两次,那么 \(fa_i,i\) 就满足转移关系。因为 \(endpos\) 集合中每个串本质相同,所以这个 \(p\) 取随意一个位置即可。程序中取的第一个位置。
此处的转移也可以说明“能选就选”的贪心是正确的。假设点集 \(\{u_1,u_2...u_i\}\) 都可以被选作状态中的第 \(k\) 个点,因为状态的转移依赖于 \(endpos\) 集合,而这些点集的 \(endpos\) 集合是包含关系,深度越浅的点 \(endpos\) 集合越大,所以取得深度最浅的点为第 \(k\) 个点肯定不会使得接下来的转移更劣
然后再用线段树合并跑出每个节点 \(endpos\) 集合判断转移即可。注意要用 \(g_u\) 记录下最后转移的节点啊
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
int n; string s;
int rt[N<<1];
struct Segment_Tree
{
struct node { int ls,rs,sum; }tr[N<<3];
int cnt=0;
void insert(int &id,int l,int r,int pos)
{
id=++cnt; tr[id].sum=1;
if (l==r) return ; int mid=(l+r)>>1;
if (mid>=pos) insert(tr[id].ls,l,mid,pos);
else insert(tr[id].rs,mid+1,r,pos);
}
int merge(int lrt,int rrt,int l,int r)
{
if (!lrt||!rrt) return lrt+rrt;
int k=++cnt; tr[k].sum=tr[lrt].sum|tr[rrt].sum;
if (l==r) return k; int mid=(l+r)>>1;
tr[k].ls=merge(tr[lrt].ls,tr[rrt].ls,l,mid);
tr[k].rs=merge(tr[lrt].rs,tr[rrt].rs,mid+1,r);
return k;
}
int query(int id,int l,int r,int ql,int qr)
{
if (!id) return 0;
if (l>=ql&&r<=qr) return tr[id].sum;
int mid=(l+r)>>1,res=0;
if (mid>=ql) res|=query(tr[id].ls,l,mid,ql,qr);
if (mid+1<=qr) res|=query(tr[id].rs,mid+1,r,ql,qr);
return res;
}
}Tr;
struct sam
{
struct node{ int len,fa,son[26]; }d[N<<1];
int lst=1,cnt=1;
int f[N<<1],g[N<<1];
void insert(int c)
{
int p=lst,np=lst=++cnt;
d[np].len=d[p].len+1; pos[np]=d[np].len;
for (;p&&!d[p].son[c];p=d[p].fa) d[p].son[c]=np;
if (!p) { d[np].fa=1; return ; }
int q=d[p].son[c];
if (d[q].len==d[p].len+1) { d[np].fa=q; return ; }
int nq=++cnt; d[nq]=d[q]; pos[nq]=pos[q];
d[nq].len=d[p].len+1,d[q].fa=d[np].fa=nq;
for (;p&&d[p].son[c]==q;p=d[p].fa) d[p].son[c]=nq;
}
int sum[N<<1],tmp[N<<1],pos[N<<1];
int get_ans()
{
//基数排序跑出树的 dfn 序
int res=1,p=1;
for (int i=1;i<=cnt;i++) sum[d[i].len]++;
for (int i=1;i<=n;i++) sum[i]+=sum[i-1];
for (int i=1;i<=cnt;i++) tmp[sum[d[i].len]--]=i;
for (int i=1;i<=n;i++) Tr.insert(rt[p=d[p].son[s[i]-'a']],1,n,i);
for (int i=cnt;i>=1;i--) rt[d[tmp[i]].fa]=Tr.merge(rt[d[tmp[i]].fa],rt[tmp[i]],1,n);
for (int i=1;i<=cnt;i++)
{
if (d[tmp[i]].fa==1) { f[tmp[i]]=1; g[tmp[i]]=tmp[i]; continue; }
if (!d[tmp[i]].fa) continue;
if (Tr.query(rt[g[d[tmp[i]].fa]],1,n,pos[tmp[i]]-d[tmp[i]].len+d[g[d[tmp[i]].fa]].len,pos[tmp[i]]-1)) f[tmp[i]]=f[d[tmp[i]].fa]+1,g[tmp[i]]=tmp[i];
else f[tmp[i]]=f[d[tmp[i]].fa],g[tmp[i]]=g[d[tmp[i]].fa]; res=max(res,f[tmp[i]]);
}
return res;
}
}sm;
signed main()
{
freopen("ea.in","r",stdin);
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>s; s=" "+s;
for (int i=1;i<=n;i++) sm.insert(s[i]-'a');
cout<<sm.get_ans(); return 0;
}
P4770 [NOI2018] 你的名字
先考虑在整个串上怎么跑出答案。
刚开始有个非常 naive 的想法,是先用跑 LCP 的方式跑出 \(f_i\),最终答案看似是 \(\sum i-f_i\) 但这之中可能会有本质相同的子串,所以考虑将其放到 \(t\) 串的 SAM 上统计答案
现在在 \(t\) 串 SAM 的每个节点处维护一个 \(ans=f_{pos}\),那么该点维护的信息如下图
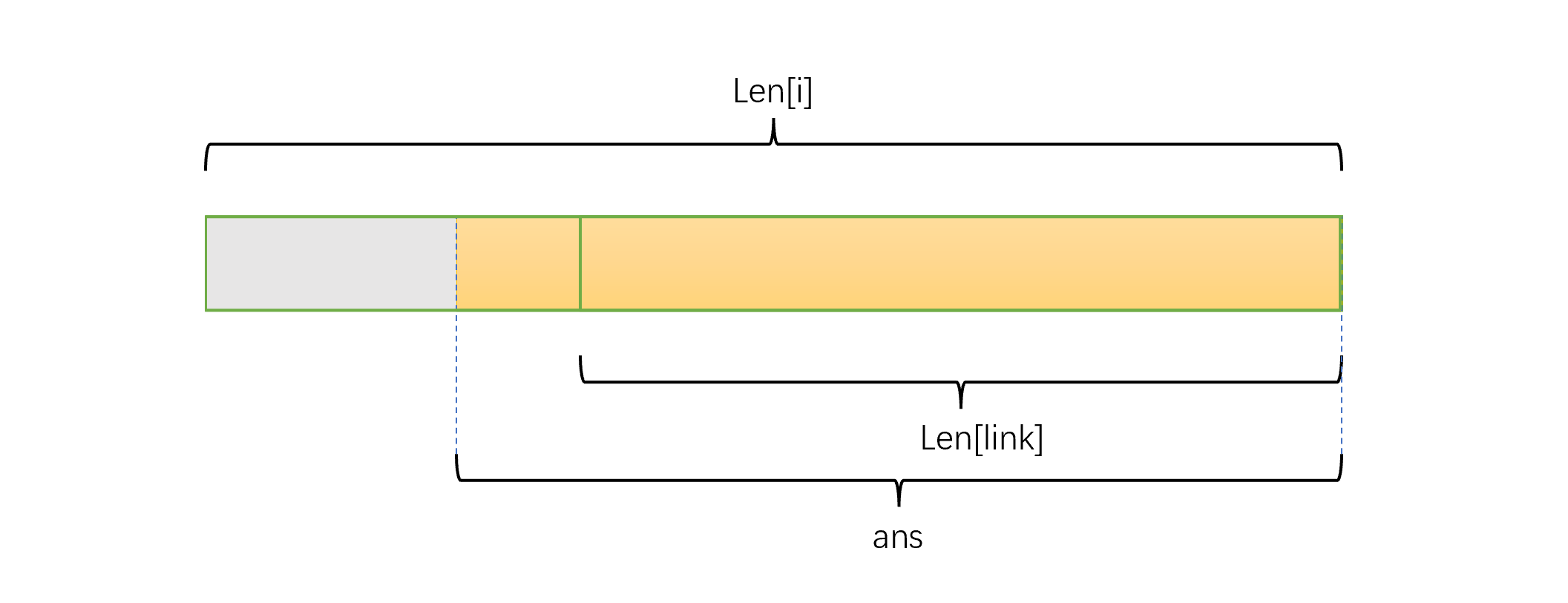
该节点表示的子串中,不是 \(s\) 的子串的就是上图的灰色部分,即 \(len_i-ans\);但可能存在 \(ans<len_{fa}\) 的情况,即该节点的 \(len_i-len_{fa}\) 个子串都不是 \(s\) 的子串,所以其贡献应该是 \(min(len_i-ans,len_i-len_{fa})\)。
现在考虑在 \(s[l...r]\) 上跑出答案。仍是先在 \(s\) 串上跑匹配,此时失配条件应是没有出边 \(c\) 或 \(endpos_u\cap[l,r]=\varnothing\)。设当前节点为 \(u\),判完失配后会得到当前匹配长度 \(len\),这是 \(f_i\) 不考虑左边界 \(l\) 的上界。设 \(x\) 为其 \(endpos\) 集合在 \([l,r]\) 区间中最靠右的元素,那么 \(u\) 子串在 \([l,r]\) 的长度贡献为 \(min(len_u,x-l+1)\),但是当前跳到的 \(u\) 可能不是贡献最大的节点,所以还需继续跳 \(link\)。
但一直跳到头的复杂度显然是不对的,观察 \(min(len_u,x-l+1)\),发现跳 \(link\) 的过程中 \(len\) 单调递减,\(x-l+1\) 单调不减,所以其函数图像是 “\(\land\)” 形,跳到单峰时(即 \(len<x-l+1\) 时)取到最大值停止即可。需要注意是否可以取到上界 \(len\)
维护 \(endpos\) 集合仍是上可持久化线段树合并。复杂度打底为 \(O(n\log n)\),实则 \(O(\)能过\()\)。注意代码细节
代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=5e5+5;
string s,t;
int n,q,m,rt[N<<1],f[N];
struct Segment_Tree
{
struct node { int ls,rs,sum; }tr[N<<8];
int cnt=0;
void insert(int &id,int l,int r,int pos)
{
if (!id) id=++cnt;
tr[id].sum=1;
if (l==r) return ;
int mid=(l+r)>>1;
if (mid>=pos) insert(tr[id].ls,l,mid,pos);
else insert(tr[id].rs,mid+1,r,pos);
}
int merge(int lrt,int rrt,int l,int r)
{
if (!lrt||!rrt) return lrt|rrt;
int k=++cnt; tr[k].sum=tr[lrt].sum|tr[rrt].sum;
if (l==r) return k;
int mid=(l+r)>>1;
tr[k].ls=merge(tr[lrt].ls,tr[rrt].ls,l,mid);
tr[k].rs=merge(tr[lrt].rs,tr[rrt].rs,mid+1,r);
return k;
}
int query(int id,int l,int r,int ql,int qr)
{
if (!tr[id].sum||r<ql||l>qr) return 0;
if (l==r) return l;
int mid=(l+r)>>1,res=0;
if (mid+1<=qr&&tr[tr[id].rs].sum) res=query(tr[id].rs,mid+1,r,ql,qr);
return (res?res:(mid>=ql&&tr[tr[id].ls].sum?query(tr[id].ls,l,mid,ql,qr):0));
}
}Tr;
struct sam
{
struct node { int ch[26],fa,len,pos; }d[N<<1];
int lst=1,cnt=1;
vector <int> tr[N<<1];
void init() { for (int i=1;i<=cnt;i++) memset(d[i].ch,0,sizeof d[i].ch); lst=cnt=1; }
void insert(int c,int id)
{
int p=lst,np=lst=++cnt;
d[np].len=d[p].len+1; d[np].pos=id;
for (;p&&!d[p].ch[c];p=d[p].fa) d[p].ch[c]=np;
if (!p) { d[np].fa=1; return ; }
int q=d[p].ch[c];
if (d[q].len==d[p].len+1) { d[np].fa=q; return ; }
int nq=++cnt; d[nq]=d[q];
d[nq].len=d[p].len+1; d[q].fa=d[np].fa=nq;
for (;p&&d[p].ch[c]==q;p=d[p].fa) d[p].ch[c]=nq;
}
void dfs(int x)
{
int _size=tr[x].size(),v;
for (int i=0;i<_size;i++) { dfs(v=tr[x][i]); rt[x]=Tr.merge(rt[x],rt[v],1,n); }
}
void build()
{
int x=1;
for (int i=1;i<=n;i++) Tr.insert(rt[x=d[x].ch[s[i]-'a']],1,n,i);
for (int i=1;i<=cnt;i++) tr[d[i].fa].push_back(i);
dfs(1);
}
void lcp(int l,int r)
{
int x=1,len=0,tmp,pre;
for (int i=1;i<=m;i++)
{
int c=t[i]-'a';
while (x&&!d[x].ch[c]) { x=d[x].fa; len=d[x].len; }
if (!x) { x=1; f[i]=len=0; continue; }
x=d[x].ch[c]; len++;
while (!Tr.query(rt[x],1,n,l,r)) { x=d[x].fa; len=d[x].len; }
if (x==1) { f[i]=len=0; continue; }
f[i]=len; pre=x;
while (x&&(tmp=Tr.query(rt[x],1,n,l,r))-l+1<=d[x].len&&tmp-l+1<=len) { f[i]=min(tmp-l+1,d[x].len); pre=x; x=d[x].fa; }
if (f[i]<=min({d[x].len,len,tmp-l+1})) { f[i]=min({d[x].len,len,tmp-l+1}); pre=x; }
x=pre; len=f[i];
}
}
ll get_ans()
{
ll res=0;
for (int i=1;i<=cnt;i++) res+=max(min(d[i].len-d[d[i].fa].len,d[i].len-f[d[i].pos]),0);
return res;
}
}sm1,sm2;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>s>>q; n=s.size(),s=" "+s; sm1.init();
for (int i=1;i<=n;i++) sm1.insert(s[i]-'a',i);
sm1.build(); int l,r;
while (q--)
{
cin>>t>>l>>r; m=t.size(),t=" "+t; sm2.init();
for (int i=1;i<=m;i++) sm2.insert(t[i]-'a',i);
sm1.lcp(l,r); cout<<sm2.get_ans()<<"\n";
}
return 0;
}
前置芝士:广义SAM
广义 SAM 存在若干假写法,假写法有:
- 给文本串中间加上分隔符后跑普通 SAM。这种的限制在于分隔符需要互不相同,当串串数量很多时串串的字符集会变大,SAM 的线性复杂度基于“字符集大小为常数”,所以该做法不保证时间复杂度
- 每插完一个串串就将 \(lst\) 变成 \(1\)。这种插入方法可能产生空节点(可能会重复给 \(lst\) 插入边 \(c\),此时它就会变成空有 \(link\) 没有入度的空节点),影响 \(parent\) 树统计子树大小,所以在部分题目中不保证正确性
正确写法是将所有串串建成 Trie 树后根据 Trie 树建 SAM(Trie 树可以避免相同前缀的重复插入)。此时的 \(endpos\) 集合定义略有变化:
- 对于字符串 \(s\),定义其 \(endpos\) 集合为 \(\{y|S(x,y)=s,y\in subtree(x)\}\)。其中 \(S(x,y)\) 表示 Trie 树上从节点 \(x\) 到节点 \(y\) 的路径形成的串
广义 SAM 更像是将 Trie 树上的节点放到 SAM 上,所以当插入节点 \(x\) 时 SAM 中的记录的 \(lst\) 节点应是 \(fa_x\) 在 SAM 中的节点。
可以离线 bfs 实现,或者 dfs 加特判
int insert(int c,int lst)
{
int np=++cnt,p=lst;
d[np].len=d[p].len+1;
for (;p&&!d[p].ch[c];p=d[p].fa) d[p].ch[c]=np;
if (!p) { d[np].fa=1; return np; }
int q=d[p].ch[c];
if (d[q].len==d[p].len+1) { d[np].fa=q; return np; }
int nq=++cnt; d[nq]=d[q];
d[nq].len=d[p].len+1; d[np].fa=d[q].fa=nq;
for (;p&&d[p].ch[c]==q;p=d[p].fa) d[p].ch[c]=nq;
return np;
}
void bfs()
{
for (int i=0;i<26;i++) if (tr[1].ch[i]) q.push({tr[1].ch[i],1});
while (!q.empty())
{
pii t=q.front(); q.pop();
int id=sm.insert(tr[t.fst].c,t.scd);
for (int i=0;i<26;i++) if (tr[t.fst].ch[i]) q.push(mkp(tr[t.fst].ch[i],id));
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号