SAM 学习笔记
1.基本概念
SAM 是个 DAG 。它存在一个源点 \(t_0\) 与多个终止状态,每条边都代表着一个字符。从源点到每个终止状态的路径代表着原串的一个后缀,所以在 SAM 上可以找到原串的所有子串(后缀的前缀)。
SAM 的点数上限为 \(2n-1\),边数上限为 \(3n-4\),时空复杂度均为 \(O(n)\),证明留坑
endpos: 一个子串的 \(endpos\) 就是其在原串中结束位置的集合。比如 \(s= ''ababc\ '',endpos(''ab'')=\{2,4\}\)
容易发现,有一些子串的 \(endpos\) 集合相同,这些子串存在后缀关系,被称为“等价类”。
link: 一个串的 \(link\) 是该串中 \(endpos\) 与该串不同的最长后缀
例如:对于字符串 \(s=''ababc'',link(''abab'')=''ab''\)
性质1: 字符串 \(s\) 的两个非空子串 \(u\) 和 \(w\)(假设 \(\left|u\right|\le \left|w\right|\))的 \(\operatorname{endpos}\) 相同,当且仅当字符串 \(u\) 在 \(s\) 中的每次出现,都是以 \(w\) 后缀的形式存在的。
性质2: 考虑两个非空子串 u 和 w(假设 \(\left|u\right|\le \left|w\right|\))。若 \(u\) 是 \(w\) 的一个后缀,那么\(\operatorname{endpos}(w) \subseteq \operatorname{endpos}(u)\);否则 \(\operatorname{endpos}(w) \cap \operatorname{endpos}(u) = \varnothing\)。
性质3:对于同一等价类的任一两子串按长度排序,较短者为较长者的后缀,且较短者的长度恰好比较长者少一
性质4:所有的 \((p,link(p))\) 会形成一棵根为 \(t_0\) 的树,且父节点的 \(endpos\) 集合包含子节点的 \(endpos\) 集合
构造
void insert(int c)
{
int p=lst,np=lst=++cnt;
d[np].len=d[p].len+1;
for (;p&&!d[p].ch[c];p=d[p].fa) d[p].ch[c]=np;
//现在相当于是要在先前所有的不完整后缀上再插入字符 c ,上面一行就是枚举后缀
//下文确认 link 需分讨
if (!p) { d[np].fa=1; return ; }//此时说明新字符串的所有后缀先前都没有出现过,不会改变 endpos 集合
int q=d[p].ch[c];
if (d[q].len==d[p].len+1) { d[np].fa=q; return ; }
//这很难理解了。反正下面的情况需要给q掰成两半
int nq=++cnt;
d[nq]=d[q];
d[nq].len=d[p].len+1,d[q].fa=d[np].fa=nq;
for (;p&&d[p].ch[c]==q;p=d[p].fa) d[p].ch[c]=nq;
}
2.题目
P3804 【模板】后缀自动机(SAM)
某个子串的出现次数就是其 \(endpos\) 集合大小。在 \(parent\) 树上 DP 求出每个状态的 \(endpos\) 集合大小再乘上其子串长度取最大值就是最终答案
SP1811 LCS - Longest Common Substring
对一个串建 SAM ,考虑用另一串的前缀匹配 SAM 。记当前所在节点 \(now\) 以及当前长度 \(len\) ,若当前能直接匹配就直接 \(len+1\) ,否则跳到 \(link(now)\) 继续匹配(此时 \(len\) 变为 \(link(now)\) 长度)
void init()
{
int now=1,len=0;
for (int i=1;i<=n;i++)
{
int c=(int)(s[i]-'a');
if (d[now].ch[c]) { f[i]=++len; now=d[now].ch[c]; continue; }
while (now&&!d[now].ch[c]) { now=d[now].fa; len=d[now].len; }
if (!now) now=1;
else { f[i]=++len; now=d[now].ch[c]; }
}
}
P6640 [BJOI2020] 封印
首先将 \(s\) 与 \(t\) 的 SAM 匹配。对于查询 \(l,r\),答案就是 \(max\{min(i-l+1,f_i)\}\) 。考虑 \(f_i\) 贡献的条件,当 \(i-f_i+1>l\) 时 \(f_i\) 贡献;发现 \(i-f_i+1\) 单调不降,那么好二分查询+区查最大值做完了
P3975 [TJOI2015] 弦论
肯定要在 SAM 上 DP 求出每个节点的子串个数,然后寻找包含第 \(k\) 小的节点。
若 \(t=0\) ,那么视作每个串出现一次;否则在 \(parent\) 树上 DP 求出每个串出现次数并给 DP 数组赋初值
void get_ans(int x,int k)
{
if (k<=0) return ;
for (int i=0;i<26;i++)
{
int v=d[x].ch[i];
if (!v) continue;
if (f[v]<k) { k-=f[v]; continue; }
ans+=(char)(i+'a');
get_ans(v,k-(t==0?1:d[v].siz));
break;
}
}
CF1063F String Journey
关于程序实现:
翻转字符串的好处就是在寻找 \(s[i-f_i+1,i]=s[j-f_j+1,j]\) 或 \(s[i-f_i,i-1]=s[j-f_j+1,j]\) 时可以直接查询 \(s[i]\) 与 \(s[i-1]\) 的后缀。
具体地, \(link(s)\) 一定是 \(s\) 的后缀,同时在 \(parent\) 树上,\(link(s)\) 子树的节点一定都包含 \(link(s)\) 。所以,这题需要找到 \(s[i-f_i+1]\) (或另一种),就在 \(parent\) 树上从 \(s\) 串的节点一直往上跳祖先,这时的限制就转为了长度的限制。
思路
题目思路大概是一些性质组成的
- 一定存在一种 \(|t_1|=1,|t_2|=2...|t_k|=k\) 的最优方案。因为一个最优方案一定可以通过删去某些
不重要的字符使其长度递增。那么显然有 \(t_i=t_{i-1}+c\) 或 \(t_i=c+t_{i-1}\),即其要么是在转移串前补个字符,要么是在之后补个字符
DP 状态为最后一串以第 \(i\) 位结尾的串组个数。考虑转移。
- \(i-dp_i+1\) 单调不减(即最后的串开始位置单调不降)。若该条件不成立,那么 \(f_i\) 最后的串会包含 \(f_{i-1}\) 的串,若 \(f_{i-1}\) 合法,一定可以通过删去 \(f_i\) 的一些字符使得其满足该条性质且合法
废话连篇
这样可以用双指针维护,缩小枚举范围
假设现在正在枚举 \(s[r,i]\) 作为 \(f_i\) 的最后一个串。若其合法,那么一定存在 \(j\) 满足性质 1 以及 \(f_j\geqslant i-r\)
满足性质 1 是因为要满足子串关系,第二个东西是因为 \(f_j\) 的最小值是 \(r-i\) (因为我们钦定相邻串长差 1 ),若 \(f_j\) 大于这个值,那么一定存在删字符的方式使得其变成 \(r-i\)
那么,在 \(parent\) 树上寻找满足性质 1 的 \(j\),再在其子树内维护 \(f_j\) 的最大值(线段树维护)判断就行了
啊。
#include <bits/stdc++.h>
using namespace std;
const int N=5e5+5;
int n;
int f[N],r,ans;
string str;
vector <int> tr[N<<1];
int id[N],dfn[N<<1],siz[N<<1],cntt;
struct SAM{
struct node{
int fa,len;
int ch[26];
}d[N<<1];
int cnt=1,lst=1;
inline void insert(int c,int i)
{
int p=lst,np=lst=++cnt;
id[i]=np,d[np].len=d[p].len+1;
for (;p&&!d[p].ch[c];p=d[p].fa) d[p].ch[c]=np;
if (!p) { d[np].fa=1; return ; }
int q=d[p].ch[c];
if (d[q].len==d[p].len+1) { d[np].fa=q; return ; }
int nq=++cnt;
d[nq]=d[q];
d[nq].len=d[p].len+1,d[q].fa=d[np].fa=nq;
for (;p&&d[p].ch[c]==q;p=d[p].fa) d[p].ch[c]=nq;
}
inline void init() { for (int i=2;i<=cnt;i++) tr[d[i].fa].push_back(i); }
int st[N<<1][21];
void dfs(int x)
{
siz[x]=1,dfn[x]=++cntt;
int _size=tr[x].size();
for (int i=0;i<_size;i++) { dfs(tr[x][i]); siz[x]+=siz[tr[x][i]]; }
}
inline void initST()
{
for (int i=1;i<=cnt;i++) st[i][0]=d[i].fa;
for (int j=1;j<=20;j++)
for (int i=1;i<=cnt;i++) st[i][j]=st[st[i][j-1]][j-1];
}
inline int get(int x,int len)
{
for (int i=20;i>=0;i--) if (st[x][i]&&d[st[x][i]].len>=len) x=st[x][i];
return x;
}
}sm;
struct Segment_Tree
{
struct node{
int l,r;
int mx;
}tr[N<<3];
inline void push_up(int id) { tr[id].mx=max(tr[id<<1].mx,tr[id<<1|1].mx); }
void build(int id,int l,int r)
{
tr[id].l=l,tr[id].r=r;
if (l==r) return ;
int mid=(l+r)>>1;
build(id<<1,l,mid),build(id<<1|1,mid+1,r);
}
void update(int id,int pos,int val)
{
if (tr[id].l==pos&&tr[id].r==pos) { tr[id].mx=val; return ; }
int mid=(tr[id].l+tr[id].r)>>1;
if (pos<=mid) update(id<<1,pos,val);
else update(id<<1|1,pos,val);
push_up(id);
}
int query(int id,int l,int r)
{
if (tr[id].l>=l&&tr[id].r<=r) return tr[id].mx;
int mid=tr[id].l+tr[id].r>>1,res=0;
if (mid>=l) res=max(res,query(id<<1,l,r));
if (mid+1<=r) res=max(res,query(id<<1|1,l,r));
return res;
}
}Tr;
bool check(int i)
{
int p1=sm.get(id[i],f[i]-1),p2=sm.get(id[i-1],f[i]-1);
int mx=0;
if (p1) mx=Tr.query(1,dfn[p1],dfn[p1]+siz[p1]-1);
if (p2) mx=max(Tr.query(1,dfn[p2],dfn[p2]+siz[p2]-1),mx);
return mx>=f[i]-1;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>str;
str=" "+str;
for (int i=1;i<=n/2;i++) swap(str[i],str[n-i+1]);
for (int i=1;i<=n;i++) sm.insert(str[i]-'a',i);
sm.init(),sm.dfs(1),sm.initST(),Tr.build(1,1,cntt);
for (int i=1;i<=n;i++)
{
f[i]=f[i-1]+1;
while (!check(i)) { f[i]--; r++; Tr.update(1,dfn[id[r]],f[r]); }
ans=max(ans,f[i]);
}
cout<<ans;
return 0;
}
CF700E Cool Slogans
结论:一定存在一种最优的构造方式使得 \(s_{i-1}\) 是 \(s_i\) 的后缀
首先容易发现,一定存在一种最优解使得 \(s_{i-1}\) 是 \(s_i\) 的 border,但在这道题中 \(s_{i-1}\) 与 \(s_i\) 的后缀关系更加重要,border 关系在这道题里没啥用
先根据串建出 SAM,因为前后的后缀关系,可以发现 \(s_{i-1}\) 代表的节点一定是 \(s_{i}\) 节点的祖先,所以考虑在 \(parent\) 树上 DP,由父节点向子节点转移。设 \(f_i\) 为考虑从根到 \(i\) 节点的最长序列长度。若 \(f_i\) 能从 \(f_{fa_i}\) 转移而来,根据“能选就选”原则,有 \(f_{i}=f_{fa_i}+1\),否则 \(f_{i}=f_{fa_i}\)。
首先,因为一个节点内串的 \(endpos\) 集合相同,转移只关注其出现位置,所以每个点都取其最长的串不会使得结果更劣。下文中的 \(len_i\) 指 \(i\) 节点的最长串长度。
现在考虑转移条件。对于节点 \(i\) 的串的一个结尾位置 \(p\),若在上一个转移节点的 \(endpos\) 集合中 \(p\) 的前驱 \(q\) 满足包含关系
即 \(endpos\) 集合中存在元素 \(q\) 满足
此时串 \(s[q-len_{q}+1,q]\) 在 \(s[p-len_p+1,p]\) 出现了两次,那么 \(fa_i,i\) 就满足转移关系。因为 \(endpos\) 集合中每个串本质相同,所以这个 \(p\) 取随意一个位置即可。程序中取的第一个位置。
然后再用线段树合并跑出每个节点 \(endpos\) 集合判断转移即可。注意要用 \(g_u\) 记录下最后转移的节点啊
DP“能选就选”的贪心:若一条返祖链上有若干节点 \(u1,u2,...\) 都可以被选作第 \(k\) 个点,在转移下一个点时显然是第 \(k\) 个点的 \(endpos\) 集合越大越有可能转移,即选深度大的点一定比选最浅的点不优,所以出现第一个可选点就要选
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
int n; string s;
int rt[N<<1];
struct Segment_Tree
{
struct node { int ls,rs,sum; }tr[N<<3];
int cnt=0;
void insert(int &id,int l,int r,int pos)
{
id=++cnt; tr[id].sum=1;
if (l==r) return ; int mid=(l+r)>>1;
if (mid>=pos) insert(tr[id].ls,l,mid,pos);
else insert(tr[id].rs,mid+1,r,pos);
}
int merge(int lrt,int rrt,int l,int r)
{
if (!lrt||!rrt) return lrt+rrt;
int k=++cnt; tr[k].sum=tr[lrt].sum|tr[rrt].sum;
if (l==r) return k; int mid=(l+r)>>1;
tr[k].ls=merge(tr[lrt].ls,tr[rrt].ls,l,mid);
tr[k].rs=merge(tr[lrt].rs,tr[rrt].rs,mid+1,r);
return k;
}
int query(int id,int l,int r,int ql,int qr)
{
if (!id) return 0;
if (l>=ql&&r<=qr) return tr[id].sum;
int mid=(l+r)>>1,res=0;
if (mid>=ql) res|=query(tr[id].ls,l,mid,ql,qr);
if (mid+1<=qr) res|=query(tr[id].rs,mid+1,r,ql,qr);
return res;
}
}Tr;
struct sam
{
struct node{ int len,fa,son[26]; }d[N<<1];
int lst=1,cnt=1;
int f[N<<1],g[N<<1];
void insert(int c)
{
int p=lst,np=lst=++cnt;
d[np].len=d[p].len+1; pos[np]=d[np].len;
for (;p&&!d[p].son[c];p=d[p].fa) d[p].son[c]=np;
if (!p) { d[np].fa=1; return ; }
int q=d[p].son[c];
if (d[q].len==d[p].len+1) { d[np].fa=q; return ; }
int nq=++cnt; d[nq]=d[q]; pos[nq]=pos[q];
d[nq].len=d[p].len+1,d[q].fa=d[np].fa=nq;
for (;p&&d[p].son[c]==q;p=d[p].fa) d[p].son[c]=nq;
}
int sum[N<<1],tmp[N<<1],pos[N<<1];
int get_ans()
{
//基数排序跑出树的 dfn 序
int res=1,p=1;
for (int i=1;i<=cnt;i++) sum[d[i].len]++;
for (int i=1;i<=n;i++) sum[i]+=sum[i-1];
for (int i=1;i<=cnt;i++) tmp[sum[d[i].len]--]=i;
for (int i=1;i<=n;i++) Tr.insert(rt[p=d[p].son[s[i]-'a']],1,n,i);
for (int i=cnt;i>=1;i--) rt[d[tmp[i]].fa]=Tr.merge(rt[d[tmp[i]].fa],rt[tmp[i]],1,n);
for (int i=1;i<=cnt;i++)
{
if (d[tmp[i]].fa==1) { f[tmp[i]]=1; g[tmp[i]]=tmp[i]; continue; }
if (!d[tmp[i]].fa) continue;
if (Tr.query(rt[g[d[tmp[i]].fa]],1,n,pos[tmp[i]]-d[tmp[i]].len+d[g[d[tmp[i]].fa]].len,pos[tmp[i]]-1)) f[tmp[i]]=f[d[tmp[i]].fa]+1,g[tmp[i]]=tmp[i];
else f[tmp[i]]=f[d[tmp[i]].fa],g[tmp[i]]=g[d[tmp[i]].fa]; res=max(res,f[tmp[i]]);
}
return res;
}
}sm;
signed main()
{
freopen("ea.in","r",stdin);
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>s; s=" "+s;
for (int i=1;i<=n;i++) sm.insert(s[i]-'a');
cout<<sm.get_ans(); return 0;
}
P4770 [NOI2018] 你的名字
先考虑在整个串上怎么跑出答案。
刚开始有个非常 naive 的想法,是先用跑 LCP 的方式跑出 \(f_i\),最终答案看似是 \(\sum i-f_i\) 但这之中可能会有本质相同的子串,所以考虑将其放到 \(t\) 串的 SAM 上统计答案
现在在 \(t\) 串 SAM 的每个节点处维护一个 \(ans=f_{pos}\),那么该点维护的信息如下图
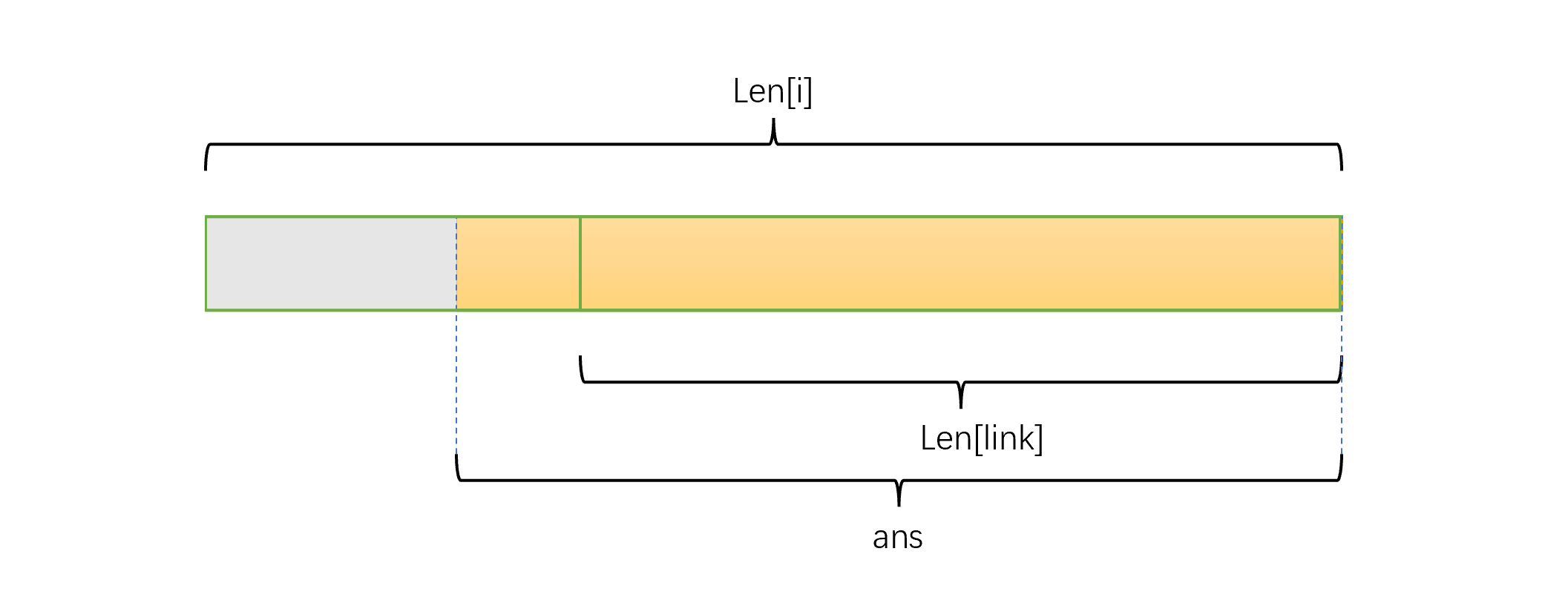
该节点表示的子串中,不是 \(s\) 的子串的就是上图的灰色部分,即 \(len_i-ans\);但可能存在 \(ans<len_{fa}\) 的情况,即该节点的 \(len_i-len_{fa}\) 个子串都不是 \(s\) 的子串,所以其贡献应该是 \(min(len_i-ans,len_i-len_{fa})\)。
现在考虑在 \(s[l...r]\) 上跑出答案。仍是先在 \(s\) 串上跑匹配,此时失配条件应是没有出边 \(c\) 或 \(endpos_u\cap[l,r]=\varnothing\)。设当前节点为 \(u\),判完失配后会得到当前匹配长度 \(len\),这是 \(f_i\) 不考虑左边界 \(l\) 的上界。设 \(x\) 为其 \(endpos\) 集合在 \([l,r]\) 区间中最靠右的元素,那么 \(u\) 子串在 \([l,r]\) 的长度贡献为 \(min(len_u,x-l+1)\),但是当前跳到的 \(u\) 可能不是贡献最大的节点,所以还需继续跳 \(link\)。
但一直跳到头的复杂度显然是不对的,观察 \(min(len_u,x-l+1)\),发现跳 \(link\) 的过程中 \(len\) 单调递减,\(x-l+1\) 单调不减,所以其函数图像是 “\(\land\)” 形,跳到单峰时(即 \(len<x-l+1\) 时)取到最大值停止即可。需要注意是否可以取到上界 \(len\)
维护 \(endpos\) 集合仍是上可持久化线段树合并。复杂度打底为 \(O(n\log n)\),实则 \(O(\)能过\()\)。注意代码细节
代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=5e5+5;
string s,t;
int n,q,m,rt[N<<1],f[N];
struct Segment_Tree
{
struct node { int ls,rs,sum; }tr[N<<8];
int cnt=0;
void insert(int &id,int l,int r,int pos)
{
if (!id) id=++cnt;
tr[id].sum=1;
if (l==r) return ;
int mid=(l+r)>>1;
if (mid>=pos) insert(tr[id].ls,l,mid,pos);
else insert(tr[id].rs,mid+1,r,pos);
}
int merge(int lrt,int rrt,int l,int r)
{
if (!lrt||!rrt) return lrt|rrt;
int k=++cnt; tr[k].sum=tr[lrt].sum|tr[rrt].sum;
if (l==r) return k;
int mid=(l+r)>>1;
tr[k].ls=merge(tr[lrt].ls,tr[rrt].ls,l,mid);
tr[k].rs=merge(tr[lrt].rs,tr[rrt].rs,mid+1,r);
return k;
}
int query(int id,int l,int r,int ql,int qr)
{
if (!tr[id].sum||r<ql||l>qr) return 0;
if (l==r) return l;
int mid=(l+r)>>1,res=0;
if (mid+1<=qr&&tr[tr[id].rs].sum) res=query(tr[id].rs,mid+1,r,ql,qr);
return (res?res:(mid>=ql&&tr[tr[id].ls].sum?query(tr[id].ls,l,mid,ql,qr):0));
}
}Tr;
struct sam
{
struct node { int ch[26],fa,len,pos; }d[N<<1];
int lst=1,cnt=1;
vector <int> tr[N<<1];
void init() { for (int i=1;i<=cnt;i++) memset(d[i].ch,0,sizeof d[i].ch); lst=cnt=1; }
void insert(int c,int id)
{
int p=lst,np=lst=++cnt;
d[np].len=d[p].len+1; d[np].pos=id;
for (;p&&!d[p].ch[c];p=d[p].fa) d[p].ch[c]=np;
if (!p) { d[np].fa=1; return ; }
int q=d[p].ch[c];
if (d[q].len==d[p].len+1) { d[np].fa=q; return ; }
int nq=++cnt; d[nq]=d[q];
d[nq].len=d[p].len+1; d[q].fa=d[np].fa=nq;
for (;p&&d[p].ch[c]==q;p=d[p].fa) d[p].ch[c]=nq;
}
void dfs(int x)
{
int _size=tr[x].size(),v;
for (int i=0;i<_size;i++) { dfs(v=tr[x][i]); rt[x]=Tr.merge(rt[x],rt[v],1,n); }
}
void build()
{
int x=1;
for (int i=1;i<=n;i++) Tr.insert(rt[x=d[x].ch[s[i]-'a']],1,n,i);
for (int i=1;i<=cnt;i++) tr[d[i].fa].push_back(i);
dfs(1);
}
void lcp(int l,int r)
{
int x=1,len=0,tmp,pre;
for (int i=1;i<=m;i++)
{
int c=t[i]-'a';
while (x&&!d[x].ch[c]) { x=d[x].fa; len=d[x].len; }
if (!x) { x=1; f[i]=len=0; continue; }
x=d[x].ch[c]; len++;
while (!Tr.query(rt[x],1,n,l,r)) { x=d[x].fa; len=d[x].len; }
if (x==1) { f[i]=len=0; continue; }
f[i]=len; pre=x;
while (x&&(tmp=Tr.query(rt[x],1,n,l,r))-l+1<=d[x].len&&tmp-l+1<=len) { f[i]=min(tmp-l+1,d[x].len); pre=x; x=d[x].fa; }
if (f[i]<=min({d[x].len,len,tmp-l+1})) { f[i]=min({d[x].len,len,tmp-l+1}); pre=x; }
x=pre; len=f[i];
}
}
ll get_ans()
{
ll res=0;
for (int i=1;i<=cnt;i++) res+=max(min(d[i].len-d[d[i].fa].len,d[i].len-f[d[i].pos]),0);
return res;
}
}sm1,sm2;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>s>>q; n=s.size(),s=" "+s; sm1.init();
for (int i=1;i<=n;i++) sm1.insert(s[i]-'a',i);
sm1.build(); int l,r;
while (q--)
{
cin>>t>>l>>r; m=t.size(),t=" "+t; sm2.init();
for (int i=1;i<=m;i++) sm2.insert(t[i]-'a',i);
sm1.lcp(l,r); cout<<sm2.get_ans()<<"\n";
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号