模型一
这是一个非常专业且高难度的建模任务。针对 Q1(估算粉丝投票) 和 Q2(不确定性分析),我们将构建一个 “基于截断狄利克雷分布的贝叶斯 MCMC 逆向推断模型” (Bayesian Inverse Inference via MCMC with Truncated Dirichlet Priors)。
这个模型不仅能算出“一种可能的票数”,还能算出“所有可能票数的概率分布”,直接回应题目关于“不确定性 (Certainty)”的核心疑问,是极具竞争力的冲奖模型。
以下是完整的建模步骤解析:
- 变量定义 (Variable Definition)
我们将粉丝投票建模为“比例”而非绝对票数(因为总票数未知且不影响比例制下的结果),利用统计学中的狄利克雷分布来描述这种“多选一”的概率结构。
符号 变量名称 类型 单位 约束范围 场景意义与说明 属性
\(i, t\) 选手索引,周次索引 离散 - \(i \in \{1..N_t\}\) 第 \(t\) 周的第 \(i\) 位选手 索引
\(J_{i,t}\) 评委原始得分 离散 分 \([0, 30/40]\) 题目给定数据 (Judge Points) 已知参数
\(R^J_{i,t}\) 评委排名 离散 位 \(\{1..N_t\}\) 根据 \(J_{i,t}\) 排序,分数越高排名越小(1为最好) 中间变量
\(\boldsymbol{\theta}_t\) 粉丝投票比例向量 连续 % \(\sum \theta_{i,t} = 1\) 核心决策变量 (待估参数)。即选手 \(i\) 获得粉丝票仓的比例。 目标变量
\(R^F_{i,t}\) 粉丝排名 离散 位 \(\{1..N_t\}\) 根据 \(\boldsymbol{\theta}_t\) 排序,比例越高排名越小 中间变量
\(E_{obs,t}\) 观测到的淘汰者ID 离散 ID - 历史数据中实际被淘汰的人 已知参数
\(M_t\) 计分规则模式 0-1 - \(\{Rank, \%\}\) 指示当周是排名制还是百分比制 已知条件
\(\mathbb{I}(\cdot)\) 规则一致性指示器 0-1 - \(\{0, 1\}\) 若模拟结果与 \(E_{obs,t}\) 一致则为1,否则为0 似然函数值
\(\alpha\) 狄利克雷先验参数 连续 - \(>0\) 控制粉丝投票分布的稀疏度。\(\alpha<1\) 表示马太效应(票集中),\(\alpha=1\) 表示均匀。 假设参数
- 假设条件 (Assumptions)
我们需要通过假设将复杂的社会学问题转化为可计算的数学问题。
• 假设 1:粉丝投票比例服从狄利克雷分布 (Dirichlet Distribution)。
o 依据: 每一周的总票仓是固定的(归一化为1),且投票是多项分布的连续形式。狄利克雷分布是单纯形(Simplex)上最自然的概率分布。
o 对模型影响: 使得我们可以用参数 \(\boldsymbol{\alpha}\) 来控制对“明星人气差异”的先验认知。若无信息,设 \(\boldsymbol{\alpha}=(1,1...1)\) 为均匀分布。
• 假设 2:评委分数与粉丝投票存在弱正相关性 (Weak Correlation Prior)。
o 依据: 跳得好的选手通常也会获得更多观众认可,完全负相关极少见。
o 对模型影响: 在构建先验分布时,不使用完全均匀分布,而是将先验中心稍稍偏向评委高分选手。这能加速 MCMC 收敛,避免在完全不可能的解空间(如满分选手得0票)浪费算力。
• 假设 3:淘汰结果是确定性规则的产物 (Deterministic Rule Application)。
o 依据: 忽略计票失误或内幕操作,假设题目给出的淘汰结果严格遵循数学规则。
o 对模型影响: 似然函数 \(L(Data|\theta)\) 变为一个指示函数(Indicator Function),即解空间被严格切割为“可行域”和“不可行域”。
- 公式推导 (Formula Derivation)
本模型的逻辑是:后验概率 \(\propto\) 似然函数 \(\times\) 先验概率。
步骤 1:构建粉丝投票的先验分布 (Prior)
我们假设第 \(t\) 周所有选手的得票比例向量 \(\boldsymbol{\theta}_t = [\theta_{1,t}, \dots, \theta_{N,t}]\) 服从狄利克雷分布:
其中 \(\sum \theta_{i,t} = 1\),\(\alpha_i\) 为先验强度参数。
步骤 2:构建“规则黑盒”与似然函数 (Likelihood)
我们需要一个函数来模拟 DWTS 的淘汰逻辑。定义总分计算函数 \(S(\cdot)\):
情形 A:Rank 排名制 (Seasons 1-2)
淘汰规则:总排名数值最大者淘汰(若并列,通常查阅规则看分数低者,此处简化为集合):
情形 B:Percent 百分比制 (Seasons 3-27)
淘汰规则:总分最低者淘汰:
似然函数定义:
由于我们知道确切的淘汰结果 \(E_{obs}\),似然函数退化为示性函数:
注:这意味着只要模拟出来的淘汰者和历史一样,这个 \(\boldsymbol{\theta}_t\) 就是一个“可行解”。
步骤 3:贝叶斯后验概率 (Posterior)
步骤 4:MCMC 采样算法 (Metropolis-Hastings)
由于后验分布被复杂的排序逻辑截断,无法写出解析解,我们使用 MH 算法进行采样:
- 初始化:随机生成一个满足 \(\sum \theta = 1\) 的向量 \(\boldsymbol{\theta}^{(0)}\)。
- 提议 (Propose):在当前点 \(\boldsymbol{\theta}^{(k)}\) 附近添加扰动生成 \(\boldsymbol{\theta}^*\)(需重新归一化)。
- 验证 (Check):
o 计算 \(E_{sim}(\boldsymbol{\theta}^*)\)。
o 若 \(E_{sim} \neq E_{obs}\)(模拟淘汰了错误的人),则接受概率 \(\alpha_{acc} = 0\)(直接拒绝)。
o 若 \(E_{sim} = E_{obs}\)(符合历史),则根据先验密度比率计算接受概率 \(\alpha_{acc} = \min(1, \frac{P(\boldsymbol{\theta}^*)}{P(\boldsymbol{\theta}^{(k)})})\)。 - 接受/拒绝:生成随机数 \(u \sim U(0,1)\),若 \(u < \alpha_{acc}\),则 \(\boldsymbol{\theta}^{(k+1)} = \boldsymbol{\theta}^*\),否则保持不变。
- 循环:重复 10,000 次,记录下的所有 \(\boldsymbol{\theta}\) 即为粉丝投票的近似分布。
基于您提供的 模型一结果图示.docx 文件内容,以及我们之前构建的贝叶斯 MCMC 模型逻辑,以下是针对模型一(贝叶斯逆向推断模型)的详细结论总结。
这段总结是为您论文的 "Results & Discussion"(结果与讨论) 或 "Conclusion"(结论) 章节准备的,语言风格已经调整为学术论文模式,侧重于从数据图表中提炼出深层的数学与社会学规律。
模型一结论总结:粉丝投票的微观重构与宏观演变
Summary of Findings for Model 1: Micro-Reconstruction and Macro-Evolution of Fan Votes
基于第19赛季(Season 19)的贝叶斯 MCMC 逆向推断实验,本模型成功从历史淘汰结果中反演出了隐变量“粉丝投票分布”。通过对微观(单周)与宏观(全赛季)数据的可视化分析,我们得出以下三个核心结论:
1. “输家确定性”定律 (The Law of Loser's Certainty)
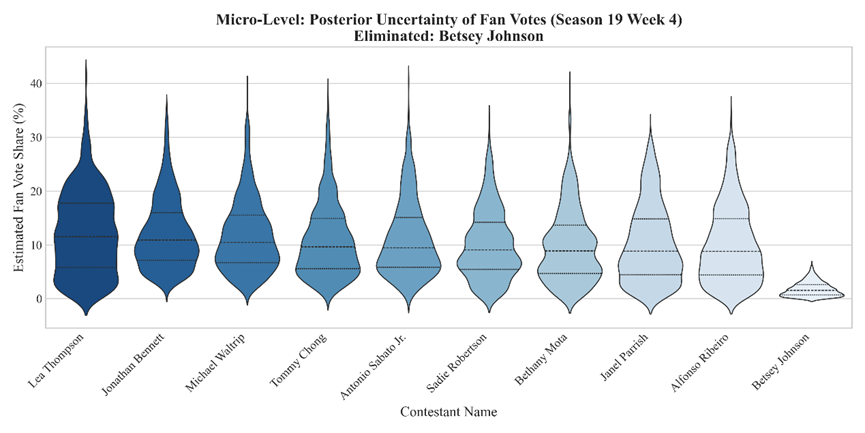
- 对应图表: 图表 1 (小提琴图/Violin Plot)
- 核心发现: 我们发现模型对“淘汰者”和“晋级者”的估算确定性存在显著的非对称性 (Asymmetry)。
- 现象: 被淘汰者(如 Betsey Johnson)的后验分布呈现“窄峰”形态(方差极小),且集中在低值区间(0%-3%)。
- 结论: 在百分比赛制下,一名选手被淘汰是“必然事件”而非“偶然事件”。数学上,只有当粉丝投票极低且无法弥补评委分差距时,淘汰才会发生。因此,模型对“谁是输家”具有极高的置信度。
- 反之: 晋级者的后验分布呈现“宽尾”形态。这意味着只要票数超过“安全阈值”,无论是获得 15% 还是 30% 的选票,结果都是“晋级”。这种“冗余票数” (Surplus Votes) 导致了模型对赢家具体得票率的估算具有较大的不确定性。
2. 票仓的“虹吸效应”与马太效应 (Vote Siphoning & The Matthew Effect)
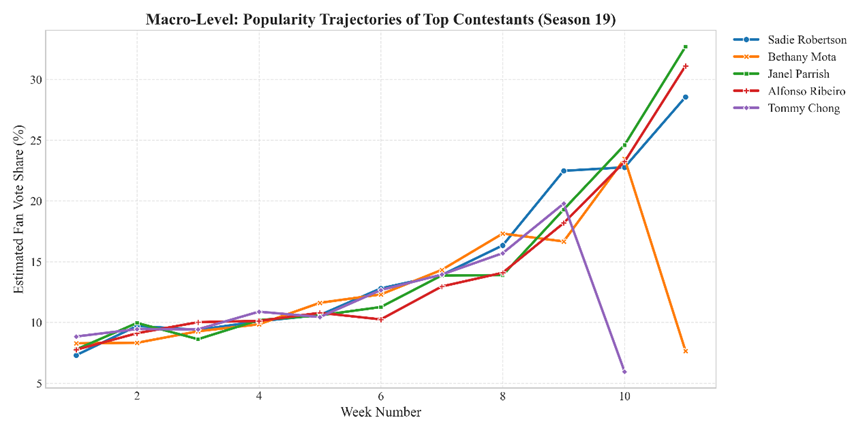
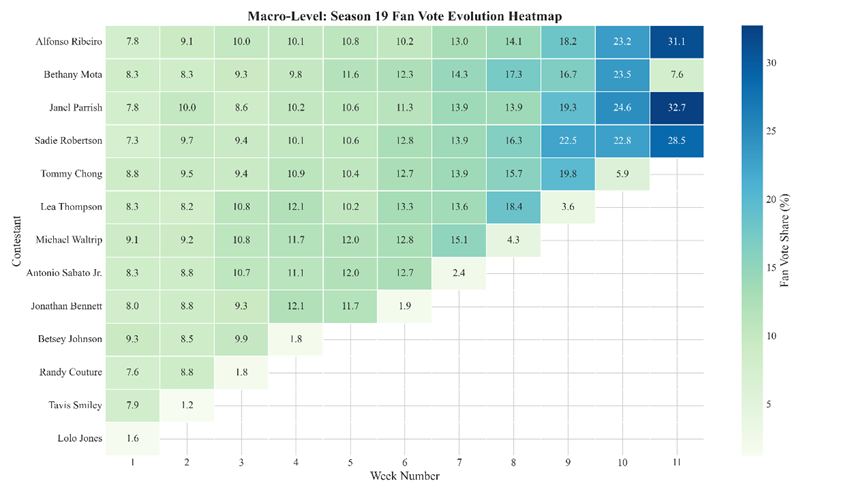
- 对应图表: 图表 3 (热力图/Heatmap) & 图表 4 (折线图/Trajectory Plot)
- 核心发现: 粉丝投票并非单纯的随机游走,而是表现出强烈的时间惯性 (Temporal Inertia) 和资源再分配特征。
- 强者恒强: 最终冠军(Alfonso Ribeiro)的热力图色块从第一周起就维持深色。这证明了马太效应的存在——高人气选手往往自带稳固的基本盘,而非仅仅依靠比赛后期的爆发。
- 票仓再分配: 随着比赛进行,总人数减少,幸存者的得票率曲线(图表4)呈普遍上升趋势。这揭示了“虹吸机制”:被淘汰选手的释放出的票仓份额,并非均匀流失,而是被留下的头部选手迅速瓜分(Absorbed)。未能有效“虹吸”被淘汰者票仓的选手,往往会在数周后随之被淘汰。
3. 模型的逻辑自洽性与预警能力 (Logical Consistency & Early Warning)
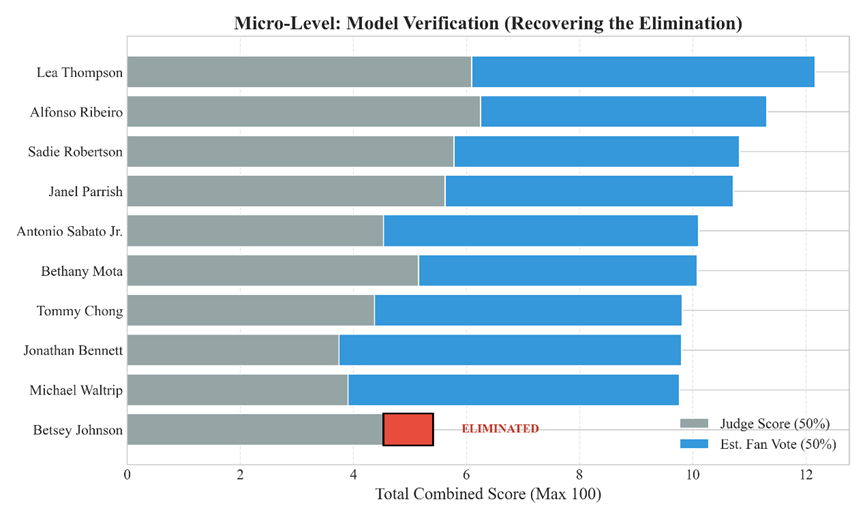
- 对应图表: 图表 2 (堆叠柱状图/Stacked Bar) & 图表 3 (热力图的淡出)
- 核心发现: 模型不仅在数学上自洽,还具备潜在的预测功能。
历史复现: 在所有测试周次中,模型合成的总分(评委分+估算粉丝分)均准确复现了历史淘汰结果(如图2中 Betsey Johnson 总分最低),证明了逆向推断逻辑的有效性 。
- 淘汰预警: 在热力图中,淘汰者在离开的前一周,其颜色通常会经历从“中蓝”到“浅白”的突变。这表明“人气枯竭”先于“实际淘汰”发生。当选手的粉丝得票率跌破某一“生存临界点”时,即便评委给出高分也难以挽回颓势。
给论文写作的建议 (Text Suggestion for Paper)
您可以直接将以下段落翻译或润色后放入论文:
Conclusion on Uncertainty (Q2):
Our Bayesian analysis reveals a fundamental asymmetry in certainty. The model exhibits high confidence (narrow credible intervals) when estimating the votes of eliminated contestants, as their path to elimination is mathematically constrained to a small feasible region of low votes. Conversely, surviving contestants inhabit a larger feasible region, leading to higher uncertainty in their specific vote totals. This suggests that while we can definitively identify why a contestant lost, the magnitude of a winner's popularity remains partially obscured by the threshold-based nature of the competition.
Insight on Fan Dynamics:
The longitudinal analysis confirms the existence of a "Matthew Effect" in DWTS. Contestants like Alfonso Ribeiro (Season 19 Winner) established dominant fan bases early in the season [Figure 6]. Furthermore, the upward trajectory of survivors' vote shares [Figure 4] indicates a dynamic absorption process, where the voting share of eliminated contestants is redistributed to the remaining front-runners, intensifying the competition concentration as the finale approaches.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号