线段树

线段树

定义

对于区间问题，如果对于区间有多次修改，并且有多次查询区间和类似的问题，如果使用暴力的方式，那么就会使复杂度达到o（n^2),对于单点修改，和区间查询，可以使用树状数组来解决，但是区间修改和区间查询，树状数组难以处理，所以我们引入线段树来维护区间信息，可以在（logn）的复杂度实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。

建树

线段树的话，通过把一个线段通过左右两边分割成两个线段，通过递归形成一个以线段（类比为树的结点）形成的树，每一个父线段（父节点，都可以由他的两个子节点组成）
比如说{a1~a8}这个线段，形成线段树方法如下

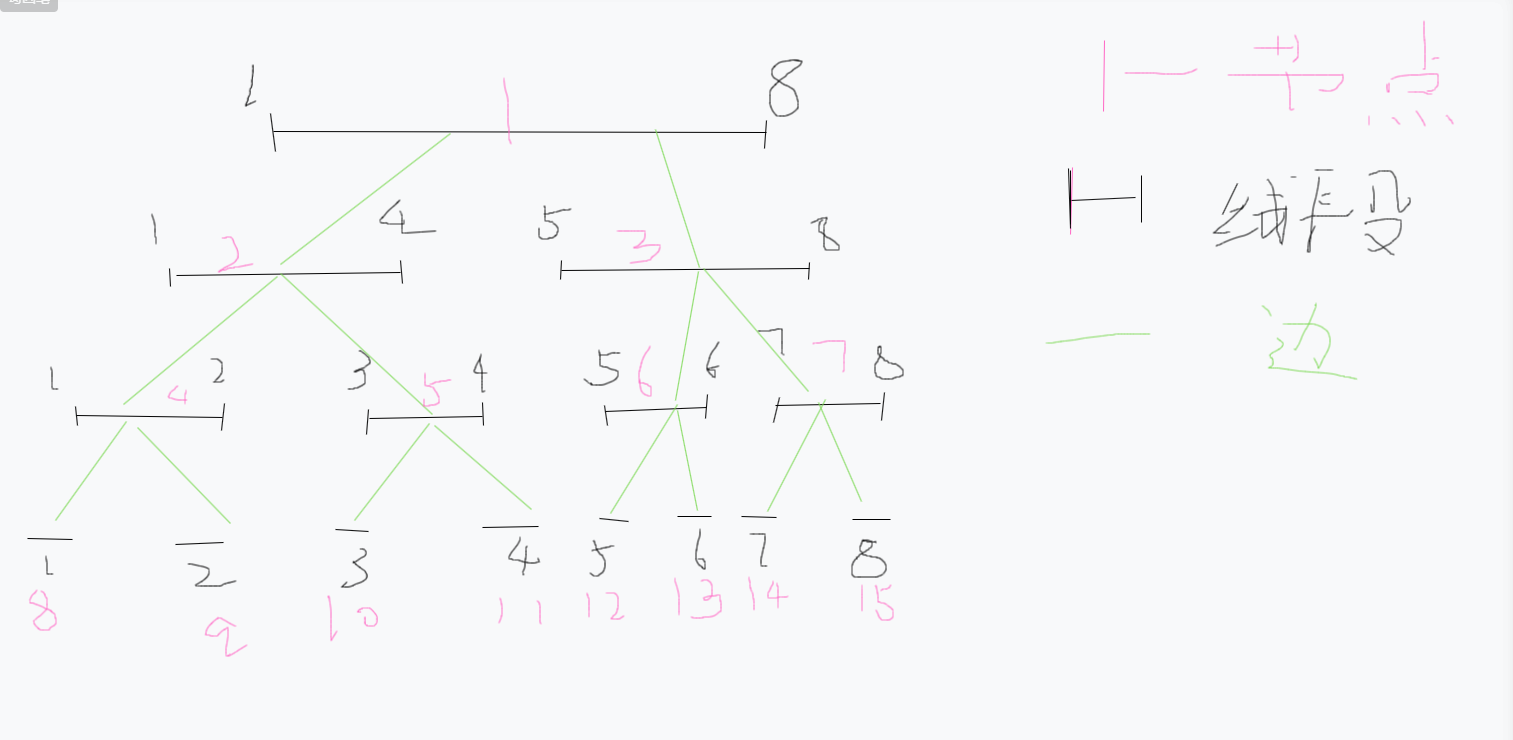
不难发现，每一个父节点di的两个子节点分别是2di与2di+1；
如果di表示的区间为[s,t],那么他的左儿子表示的区间为[s,(s+t)/2],他右儿子表示的区间为[(s+t)/2+1,t]
所以我们就可以通过递归把这个线段建成一颗树
建树代码：
（由于模板题求的是区间和，那么我们维护区间和的线段树）

void build(i64 s , i64 t , i64  p) {
	if (s == t) //如果线段已经无法分割
	{
		d [ p ] = a[s];//那么将节点的值赋值给线段树上的节点
		return;
	}
	int m = s + ( ( t - s ) >> 1 );//找到中点
	build(s , m , p * 2) , build(m + 1 , t , p * 2 + 1);//分别建左右子树
	d [ p ] = d [ p * 2 ] + d [ p * 2 + 1 ];//维护区间的和
}

区间查询

区间查询，比如求区间 [l,r] 的总和求区间最大值/最小值等操作
还是以求区间和为例子
如果我们要求区间[1,8]的和，那么我们返回第一个节点的值即可，任意一个区间，都可以由线段树上的多个节点一起表示，于是我们可以通过查询线段树上的节点，实现时间复杂度的优化，复杂度优化为（logn）

i64 getsum(i64 l , i64 r , i64 s , i64 t , i64 p) {//l，r代表查询区间左右端点，s,r代表树上节点p表示的区间范围，p代表当前树上节点p
	i64 sum = 0;//初始化值
	if (l <= s && t <= r)
		return d [ p ];//如果该节点被所查询区间包含，不必去找子节点，直接
	int m = s + ( ( t - s ) >> 1 );//找到中间点
	//找p的子节点
	if (l <= m)sum += getsum(l , r , s , m , p * 2);
	if (r > m)sum += getsum(l , r , m + 1 , t , p * 2 + 1);
	return sum;//返回答案
}

区间修改

如果要求修改区间 [l,r]，把所有包含在区间 [l,r] 中的节点都遍历一次、修改一次，时间复杂度又达到了o（n）
于是这时候我们引入一个懒惰标记
懒惰标记，简单来说，就是通过延迟对节点信息的更改，从而减少可能不必要的操作次数.因为我们每次查询答案，只查询我们所需要的区间，有些子区间不会被查询，所以我们只需要更新部分树上节点的值，用懒惰节点储存我们要更新的数据，等到我们这个子区间被查询时再采用懒惰标记更新，这样的话就可以减少操作次数。
例如我们将[4,8]这一个区间增加5，我们找到的线段树上能表示这段区间的节点分别表示[4,4],[5,8]，所以我们更新这两个节点，并且给他们的子节点传递懒惰标记，当我们查询[5,6]时，我们可以用我们的懒惰标记再去更新这个被查询区间的值，可以减少我们的运算
伪代码

void update(i64 l , i64 r , i64 c,i64 s , i64 t , i64 p) {
	if (l <= s && t <= r) { 
		d [ p ] += ( t - s + 1 ) * c , b [ p ] += c; //如果线段被更新区间包含直接更新并且，给他一个懒惰标记
		return;
	}
	int m = s + ( ( t - s ) >> 1 );
	if (b [ p ] && s != t) {//如果父节点有懒惰标记并且存在子节点
		d [ p * 2 ] += b [ p ] * ( m - s + 1 );//更新子节点的值
		d [ p * 2 + 1 ] += b [ p ] * ( t - m );//更新子节点的值
		b[p * 2] += b[p], b[p * 2 + 1] += b[p];  // 将懒惰标记下传给子节点

	}b[p] = 0;//懒惰标记用完归0
	if (l <= m)update(l , r ,c, s , m , p * 2);
	if (r > m)update(l , r ,c, m + 1 , t , p * 2 + 1);
	d [ p ] = d [ p * 2 ] + d [ p * 2 + 1 ];//计算更新后节点的值
}

通过上面的代码，基本实现了一个线段树基本功能

模板题

https://www.luogu.com.cn/problem/P3372

P3372 【模板】线段树 1

题目描述

如题，已知一个数列 \(\{a_i\}\)，你需要进行下面两种操作：

1. 将某区间每一个数加上 \(k\)。
2. 求出某区间每一个数的和。

输入格式

第一行包含两个整数 \(n, m\)，分别表示该数列数字的个数和操作的总个数。

第二行包含 \(n\) 个用空格分隔的整数 \(a_i\)，其中第 \(i\) 个数字表示数列第 \(i\) 项的初始值。

接下来 \(m\) 行每行包含 \(3\) 或 \(4\) 个整数，表示一个操作，具体如下：

1. 1 x y k：将区间 \([x, y]\) 内每个数加上 \(k\)。
2. 2 x y：输出区间 \([x, y]\) 内每个数的和。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例 #1

输入 #1

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出 #1

11
8
20

说明/提示

对于 \(15\%\) 的数据：\(n \le 8\)，\(m \le 10\)。
对于 \(35\%\) 的数据：\(n \le {10}^3\)，\(m \le {10}^4\)。
对于 \(100\%\) 的数据：\(1 \le n, m \le {10}^5\)，\(a_i,k\) 为正数，且任意时刻数列的和不超过 \(2\times 10^{18}\)。

【样例解释】

AC代码

#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
using i64 = long long;
i64 b [ 1000005 ] , a [ 1000005 ] , maxx [ 1000005 ];
i64 d[300005];
i64 n , m;
void build(i64 s , i64 t , i64  p) {
	if (s == t) //如果线段已经无法分割
	{
		d [ p ] = a[s];//那么将节点的值赋值给线段树上的节点
		return;
	}
	int m = s + ( ( t - s ) >> 1 );//找到中点
	build(s , m , p * 2) , build(m + 1 , t , p * 2 + 1);//分别建左右子树
	d [ p ] = d [ p * 2 ] + d [ p * 2 + 1 ];//维护区间的和
}
i64 getsum(i64 l , i64 r , i64 s , i64 t , i64 p) {//l，r代表查询区间左右端点，s,r代表树上节点p表示的区间范围，p代表当前树上节点p
	i64 sum = 0;//初始化值
	if (l <= s && t <= r)
		return d [ p ];//如果该节点被所查询区间包含，不必去找子节点，直接
	int m = s + ( ( t - s ) >> 1 );//找到中间点
	if (b[p])
		d[p << 1] += b[p] * (m - s + 1), d[(p << 1) | 1] += b[p] * (t - m),
		b[p << 1] += b[p], b[(p << 1) | 1] += b[p];
	b [ p ] = 0;
	//分割
	if (l <= m)sum += getsum(l , r , s , m , p * 2);
	if (r > m)sum += getsum(l , r , m + 1 , t , p * 2 + 1);
	return sum;
}
void update(i64 l , i64 r , i64 c,i64 s , i64 t , i64 p) {
	if (l <= s && t <= r) { 
		d [ p ] += ( t - s + 1 ) * c , b [ p ] += c; //如果线段被更新区间包含直接更新并且，给他一个懒惰标记
		return;
	}
	int m = s + ( ( t - s ) >> 1 );
	if (b [ p ] && s != t) {//如果父节点有懒惰标记并且存在子节点
		d [ p * 2 ] += b [ p ] * ( m - s + 1 );//更新子节点的值
		d [ p * 2 + 1 ] += b [ p ] * ( t - m );//更新子节点的值
		b[p * 2] += b[p], b[p * 2 + 1] += b[p];  // 将懒惰标记下传给子节点

	}b[p] = 0;//懒惰标记用完归0
	if (l <= m)update(l , r ,c, s , m , p * 2);
	if (r > m)update(l , r ,c, m + 1 , t , p * 2 + 1);
	d [ p ] = d [ p * 2 ] + d [ p * 2 + 1 ];//计算更新后节点的值
}
int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
		cin >> a [ i ];
	build(1 , n , 1);
	while (m--) {
		i64 x , y , z;
		cin >> x >> y >> z;
		if (x == 2) {
			cout << getsum(y , z , 1 , n , 1) << endl;
		}
		else {
			i64 c;
			cin >> c;
			update(y , z , c , 1 , n , 1);
		}
	}
}