虚树

虚树

对于一类树上DP问题，每次询问所需要查询的点为关键点，当关键点的个数与 \(n\) 是同阶的，我们可以在建虚树来解决问题。

什么是虚树？
为了提高使用关键点的效率，我们把信息浓缩，使大树变成一棵小树。

如何建虚树？

如下图，红色是我们的关键点。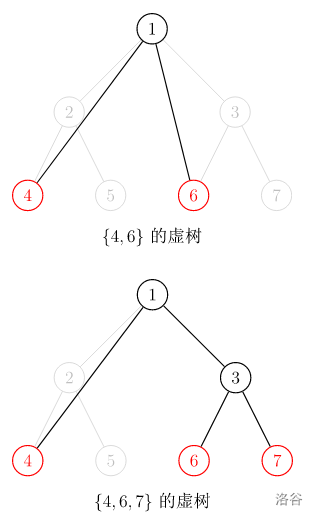

图片来源：oi-wiki。

从图中可以看出，我们需要记录关键点及连接他们的LCA，同时他们的祖先关系也没有改变。
如何更快把LCA记录下来呢，我们可以把关键点按照dfn序排序，以此记录相邻的关键点的LCA，并把它们加入。不过这样，可能会记录到相同的LCA。所以我们要再一次按照dfn序排序，同时去重。
最后，在序列上枚举相邻的两个点，求得它们的LCA，并连接LCA(x,y),y。

sort(sp+1,sp+1+K,cmp);
for(int i=1;i<K;i++){
  xu[++len]=sp[i];
  xu[++len]=lca(sp[i],sp[i+1]);
}
xu[++len]=sp[K];
sort(xu+1,xu+1+len,cmp);
len=unique(xu+1,xu+1+len)-xu-1;
for(int i=1;i<len;i++){
  int lc=lca(xu[i],xu[i+1]);
  add2(lc,xu[i+1]);
}

还可以用栈建虚树。
虚树本质好像就是去给树形DP优化？

相关题目：

P2495 [SDOI2011] 消耗战

题意：
一棵有边权的树，总部在 \(1\) 号节点，每次选择 \(m\) 个节点有资源（不在 \(1\) 节点），问断掉哪些边可以使得资源无法到达 \(1\) 号节点？断边的花费是该边边权，求最小花费。\(N\leq 300000\), \(q\leq 300000\), \(\sum^q_{i=1}m_i \leq 300000\)。
思路：
发现 \(m\) 总和与 \(n\) 同阶，我们对于每次询问建虚树，在虚树上跑树形DP。一棵虚树上有关键点和非关键点，DP时要分开讨论。对于关键点，断开它的 \(f_i=到根的最短边权\)，非关键点：\(f_i=min(到根的最短边权,f_v总和)\) 。
code：MYJ_aiie
提示：

1. 虚树个数是 \(2n-1\),数组记得开二倍。

P4103 [HEOI2014] 大工程

题意：
一棵边权为1的树，在 \(2\) 个节点 \(a,b\) 之间建一条新通道需要的代价为树上 \(a,b\) 的最短路径的长度。
每次选中 \(k\) 个点，然后在它们两两之间 新建 \(\dbinom{k}{2}\) 条新通道。
对于每个选定，要分别求： 这些新通道的代价和，新通道中代价最小、最大的是多少。
\(1\le n\le 10^6,1\le q\le 5\times 10^4,\sum k\le 2\times n\)。
思路：
建虚树跑树形DP，虚树上边权就是深度差。代价和可以考虑每条边的贡献，用该子树乘剩余节点。最大最小类似求树的直径的方法。同时要注意关键点和非关键点分类讨论。

code:MYJ_aiie
提示:

1. 关键点和非关键点分类讨论

CF613D Kingdom and its Cities

题意：
一棵 \(n\) 个节点的树，\(m\) 次询问，每次给出\(k\)个点，询问将 \(k\) 个点两两间隔开所需标记的最小间隔点数，若不能间隔开，输出-1。\(n \leq 10^5,\sum k\leq n\)
思路：
观察数据范围，建虚树。DP写错WA了几发。怎么做DP？由于关键点不能标记，所以同样分类讨论。设 \(f_u\) 表示使得以u为根的子树内的点不连通，所需的点数。\(g_u\)表示该子树内有几个点和父亲直接联通--中间未被阻断。如果是关键点，则必须把子树内直接联通的点都切掉，也就是\(f_u=\sum f_v+\sum g_v\),同时\(g_u=1\)。若不是关键点，当子树内有>1g个节点与它直接相连，也就是 \(1 \leq g_u\) 时，我们必须把这个点断掉（要不然这几个点就通过该点连起来了），也就是\(f_u=\sum f_v+1,g_u=0\)。
code:
MYJ_aiie