WQS二分

WQS二分

一句话：对于凸包，二分一个直线l的斜率k使得l与凸包的切点所对应的x为题目要求的x。此时y(也就是f(x))加或减kx就是答案。

---

适用类型：

• 如果不考虑选的物品的个数限制，可以很快求出答案。
• 恰好选 k 个物品的最优代价

思路：

考虑不限制，那我们肯定可以求到一个最优值。而这个值的两侧一定不优于它。这样大概是一个凸包（？）（不会凸包，好像要打表什么的发现）。

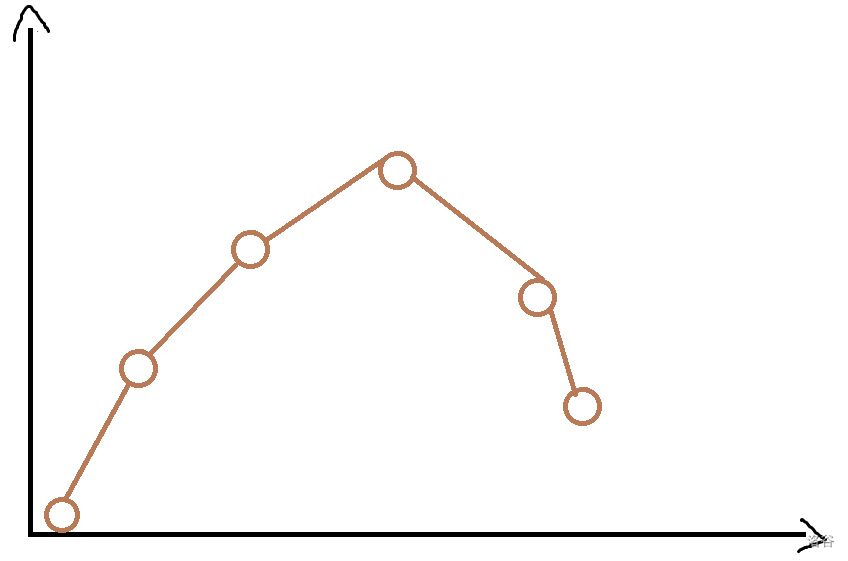
考虑一个直线与凸包的切点一定是当前斜率的最优值。为什么？我们知道 \(y=kx+b\) ，\(y\) 就是 \(f(x)\) ,也就是 \(b=f(x)-kx\) 。观察 \(b\) 的形式(只要把每次得到的权值-=k,然后正常在求任意次物品情况下的最优答案），发现截距 \(b\) 是我们要求的答案。由下图可知，相切时是最大值。

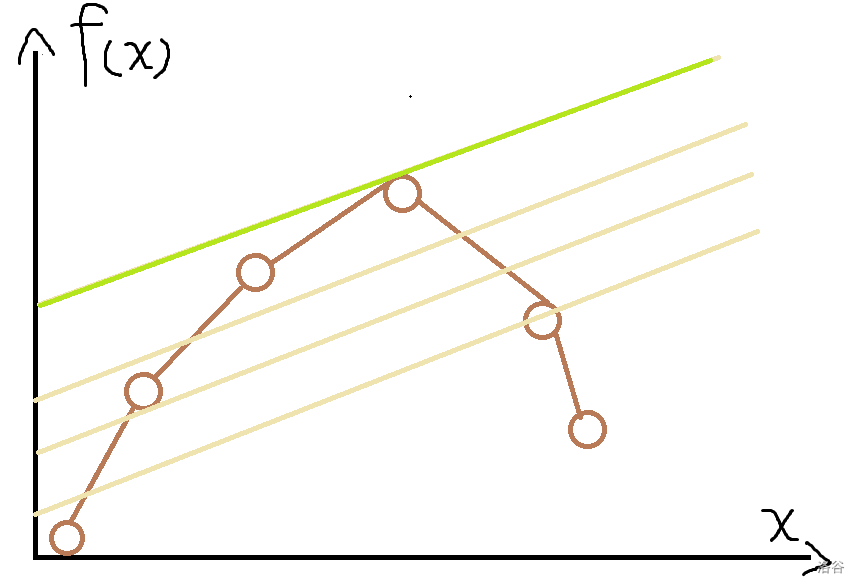
又因为，凸包切线的斜率是递增/递减的，上图为递减。所以可以二分斜率。
那么我们就通过二分斜率，使得直线与凸包相切在x=k的点上，求得答案。

例题：

P2619 [国家集训队] Tree I

思路:

不加 \(k\) 条白边限制的最小生成树肯定都会。加入我们求出来的最小生成树有 \(p\) 条白边。那么有3种情况。

• \(p=k\) RP++！（正好是答案）
• \(p<k\) 所以我们要通过减小白边权值，使得更多白边可以进入到最小生成树中。
• \(p>k\) 同上。通过增加权值，去掉多余的白边。

而我们增加或减少的值，就是要二分的。二分权值后做最小生成树，求到最小权值使得答案满足。

如何用图像来理解呢？

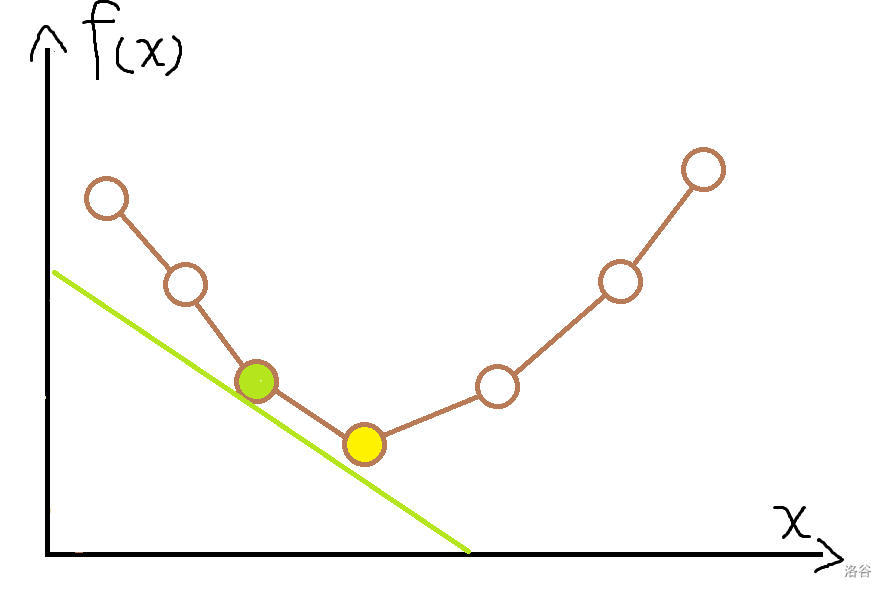
\(x\)代表选白边数量，\(f(x)\) 为此时最小生成树权值。
这是一个下凸的凸包，斜率递增。
黄点是我们无限制时的最优值。绿点是要求的。所以我们通过二分斜率来求切到它时的截距。其中\(b=f(x)-kx\) ，\(k\) 就对应我们增减的权值。

code：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+3;
int n,m,k;
struct node{
	int x,y,w,c;
}e[N];
int fa[N];
int cnt,cw,sum;
int ans;
bool cmp(node a1,node a2){//注意！ 
	if(a1.w!=a2.w)	return a1.w<a2.w;
	else return a1.c<a2.c;//边权相同时，一定要钦定先选哪条边。
}
int fat(int x){
	if(x==fa[x]) return x;
	else return fa[x]=fat(fa[x]);
}
void kru(){
	sort(e+1,e+1+m,cmp);
	for(int i=1;i<=m;i++){
		int v=e[i].x,u=e[i].y;
		v=fat(v),u=fat(u);
		if(v==u) continue;
		fa[v]=u;
		sum+=e[i].w;
		cw+=(e[i].c==0);
		cnt++;
		if(cnt==n-1) break;
	}
}
bool check(int mid){
	for(int i=1;i<=n;i++) fa[i]=i;
	cnt=cw=sum=0;
	for(int i=1;i<=m;i++){
		if(e[i].c==0) e[i].w+=mid;
	}
	kru();
	int p=0;
	if(cw>=k){
		p=1;
	}
	for(int i=1;i<=m;i++){
		if(e[i].c==0) e[i].w-=mid;
	}
	return p;
}
int main(){
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1;i<=m;i++){
		int x,y,w,c;
		scanf("%d%d%d%d",&e[i].x,&e[i].y,&e[i].w,&e[i].c);
		e[i].x++,e[i].y++;
	}
	int l=-100,r=100;
	while(l<=r){
		int mid=(l+r)>>1;
		if(check(mid)){
			l=mid+1;
			ans=mid;
		}else{
			r=mid-1;
		}
	}
	check(ans);
	printf("%d\n",sum-k*ans);
	return 0;
}