SAM
作用
对字符串 \(S\) 建立 SAM 后,SAM 可以储存 \(S\) 的所有子串信息,同时构建复杂度为 \(O(|S|)\)。
一些定义
SAM 是一个 DAG,SAM 的每一个节点被称为状态,每条边就是状态之间的转移。
SAM 存在一个节点 \(P\) 表示 SAM 上的初始节点。
SAM 的核心是 \(endpos\)(结束位置、等价类)与 \(link\)(后缀链接)。
先说 \(endpos\),定义 \(endpos(s)\) 表示串 \(s\) 在原串 \(S\) 中出现位置的末尾的集合。
例如 \(S\) 为 \(abcbc\),那么 \(endpos(bc)=\{2,4\}\)。
然后是 \(endpos\) 等价类,等价类是一个由字符串构成的集合。对于一个等价类 \(E\),满足 \(\forall s_1,s_2\in E\),有 \(endpos(s_1)=endpos(s_2)\)。
下面是一些关于 \(endpos\) 的结论。
- 对于两个非空子串 \(s1\)、\(s2\),令 \(|s_1|\ge|s_2|\),如果 \(s_1\)、\(s_2\) 的 \(endpos\) 相同,那么 \(s_2\) 是 \(s_1\) 的一个后缀。
- 对于两个非空子串 \(s1\)、\(s2\),令 \(|s_1|\ge|s_2|\),如果 \(s_2\) 是 \(s_1\) 的一个后缀,那么 \(endpos(s_1)\subset endpos(s_2)\)。
- 对于两个非空子串 \(s1\)、\(s2\),令 \(|s_1|\ge|s_2|\),如果 \(s_2\) 不是 \(s_1\) 的一个后缀,那么 \(endpos(s_1)\cap endpos(s_2)=\emptyset\)。
- 对于一个 \(endpos\) 等价类 \(E\),把里面的串按照长度从小到大排序,每一个串都是下一个串的一个后缀。
- 对于一个 \(endpos\) 等价类 \(E\),里面的串的长度是连续的。
- 一个 \(endpos\) 等价类对应 SAM 上一个节点。
接着说 \(link\)。
上面结论提到,一个等价类对应一个节点。假设这里有一个节点 \(v\),记 \(s\) 为其中最长的串。
现在有一个节点 \(u\),它的最长串为 \(t\),如果 \(t\) 为最长的 \(s\) 的一个真后缀,那么让 \(v\) 链接到 \(u\),就有 \(link(v)=u\)。
\(link\) 的实际意义就是,从某个等价类 \(E\) 不断跳 \(link\) 直到 \(P\) 就可以访问 \(E\) 中最长字符串 \(s\) 的所有后缀。
下面是一些关于 \(link\) 的结论。
- 对于一个等价类 \(E\) 满足它的最短串的长度为 \(link(E)\) 的最长串长度 \(+1\)。
- 所有后缀链接构成一棵以 \(P\) 为根的内向树(也就是 parent 树)。
对于 parent 树也有一些结论。
- parent 树与 SAM 共用同样的节点。
- 一个等价类对应 parent 树上一个节点。
建立
构建 SAM 是在线的,每次把一个字符加入 SAM,然后动态维护。
这里设 \(len(E)\) 表示这个等价类中最长字符串的长度,\(long(E)\) 表示这个等价类中的最长字符串。
最开始 SAM 中只有初始节点 \(P\),钦定 \(len(P)=0\),\(link(P)=-1\)。
现在考虑给 SAM 添加一个字符 \(c\),流程如下:
- 令 \(last\) 为添加 \(c\) 之前整个字符串 \(S\) 所对应的节点。
- 创建一个新的状态 \(cur\),将 \(len(cur)\leftarrow len(last)+1\)。
- 从 \(last\) 开始跳 \(link\),如果当前所在的节点 \(v\) 没有一条 \(c\) 的出边,那么就创建一条 \(v\to cur\) 的边。
- 如果遍历到了 \(-1\),将 \(link(cur)\leftarrow 0\)。跳到第 \(8\) 步。
- 如果当前节点 \(v\) 有一条 \(c\) 的出边,那么停止跳 \(link\),记这个节点为 \(p\),从 \(p\) 沿着 \(c\) 的这条边走到的点是 \(q\)。
- 如果说 \(len(p)+1=len(q)\),那么就说明 \(long(p)+c\) 这个字符串就是 \(long(q)\),因为 \(p\) 是第一个包含 \(c\) 这条出边的点,所以 \(long(q)\) 一定是最长的且为 \(S+c\) 的真后缀,此时就满足 \(link\) 的定义,那么将 \(link(cur)\leftarrow q\)。跳到第 \(8\) 步。
- 否则,\(long(p)+c\) 这个字符串不是 \(long(q)\),所以等价类 \(q\) 中还有更长的串,就不能直接把 \(cur\) 链接到 \(q\) 上,怎么办?考虑复制出一个节点 \(clone\),\(clone\) 拥有与 \(q\) 一样的 \(link\) 和出边,将 \(len(clone)\leftarrow len(p)+1\)。现在就可以将 \(link(cur)\leftarrow clone\),同时也要让 \(link(q)\leftarrow clone\)。修改完这个后,继续从 \(p\) 开始跳 \(link\),记当前所在节点为 \(v\),如果 \(v\) 沿着 \(c\) 这条边走到的节点为 \(q\),那么将 \(q\leftarrow clone\)。如果 \(v\) 没有 \(c\) 的出边或沿着出边走到的节点不为 \(q\),停止跳 \(link\)。跳到第 \(8\) 步。
- 将 \(last\leftarrow cur\)。跳到第 \(1\) 步。
下面是一些关于 SAM 的结论。
- 对于长度为 \(n\) 的字符串建立 SAM,SAM 中节点数不超过 \(2n-1\)。
- 对于长度为 \(n\) 的字符串建立 SAM,SAM 中边数不超过 \(3n-4\)。
- SAM 中除复制节点以外的节点,它的最长字符串代表原串的一个前缀。
- SAM 从上 \(P\) 开始走,走到的每一条不同路径都代表原串的一个子串,且每个子串只出现一次(走到终止节点的路径就是原串的后缀),特殊的,从 \(P\) 到 \(P\) 不代表任何串。
- SAM 上 \(P\) 到节点 \(u\) 的所有路径就是等价类 \(u\) 中的所有字符串。
放一张对 \(abcbc\) 建立 SAM 的图。(黑边与蓝边都表示 SAM 上的边,红边为 parent 树的边也就是每个节点的 \(link\),蓝边表示第 \(7\) 步复制节点 \(clone\) 所新添加的边)
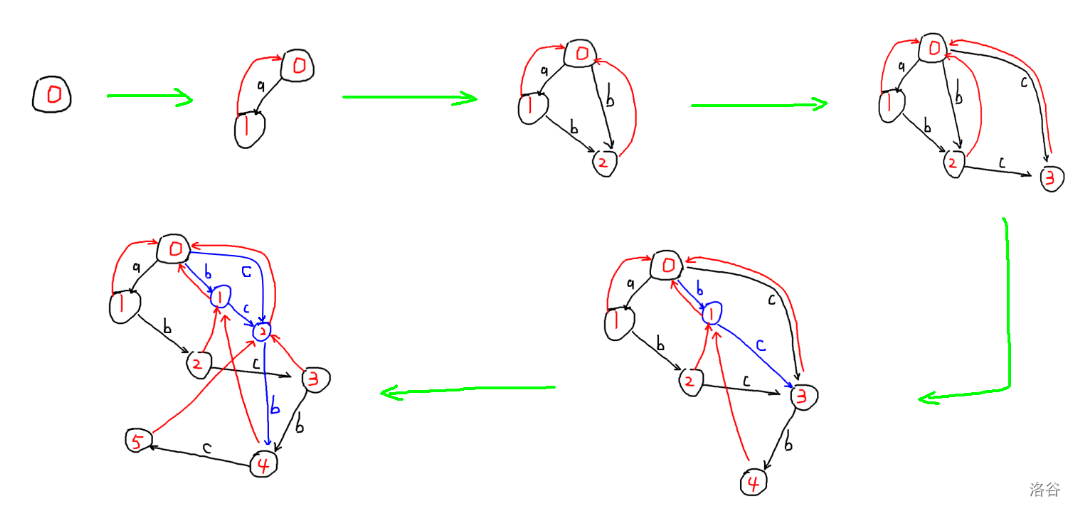
代码
struct SAM {
int tot;
int link[N], len[N];
int ch[26][N];
void init() {
for ( int i = 0; i <= tot; i ++) {
link[i] = len[i] = 0;
for ( int j = 0; j < 26; j ++)
ch[j][i] = 0;
}
tot = 0, link[0] = -1;
}
int insert( int lst, int c) {
int cur = ++ tot, p = lst, q, clone;
len[cur] = len[p] + 1;
while (p != -1 && ! ch[c][p]) ch[c][p] = cur, p = link[p];
if (p == -1) return link[cur] = 0, cur;
if (len[p] + 1 == len[q = ch[c][p]]) return link[cur] = q, cur;
clone = ++ tot, len[clone] = len[p] + 1;
link[clone] = link[q];
for ( int i = 0; i < 26; i ++) ch[i][clone] = ch[i][q];
while (p != -1 && ch[c][p] == q) ch[c][p] = clone, p = link[p];
link[cur] = link[q] = clone;
return cur;
}
} S;
代码这一块有一点改动,把 \(last\) 改成了传参式的,且每次返回新建的节点编号。这个方便解题和建立广义 SAM。
题目
【模板】后缀自动机(SAM)
模板题,要求在 \(S\) 中出现次数不为 \(1\) 的子串的出现次数乘上子串长度的最大值。
首先,对于一个节点 \(u\),也就是一个等价类 \(u\),肯定贪心的取里面最长的字符串,那么也就是 \(len(u)\)。
然后考虑每个子串的出现次数,在 SAM 上找到代表前缀的点,从它开始往上跳 \(link\),给跳到的每个点加一,也就代表这个点表示的等价类中的所有字符串都要被加一。
当然直接跳 \(link\) 复杂度较大,所以可以转化成单点加一,子树求和。
代码中的 \(pos_i\) 表示当建立了 \(S[1,i]\) 时,SAM 上的节点编号。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 2e6 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
vector< int> G[N];
int siz[N], pos[N];
struct SAM {
int tot;
int link[N], len[N];
int ch[26][N];
void init() {
for ( int i = 0; i <= tot; i ++) {
link[i] = len[i] = 0;
for ( int j = 0; j < 26; j ++)
ch[j][i] = 0;
}
tot = 0, link[0] = -1;
}
int insert( int lst, int c) {
int cur = ++ tot, p = lst, q, clone;
len[cur] = len[p] + 1;
while (p != -1 && ! ch[c][p]) ch[c][p] = cur, p = link[p];
if (p == -1) return link[cur] = 0, cur;
if (len[p] + 1 == len[q = ch[c][p]]) return link[cur] = q, cur;
clone = ++ tot, len[clone] = len[p] + 1;
link[clone] = link[q];
for ( int i = 0; i < 26; i ++) ch[i][clone] = ch[i][q];
while (p != -1 && ch[c][p] == q) ch[c][p] = clone, p = link[p];
link[cur] = link[q] = clone;
return cur;
}
} S;
long long ans;
char s[N];
void dfs( int u) {
for ( auto v : G[u]) dfs(v), siz[u] += siz[v];
if (u != 0 && siz[u] != 1) ans = max(ans, 1ll * siz[u] * S.len[u]);
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> (s + 1);
int n = strlen(s + 1);
S.init();
for ( int i = 1; i <= n; i ++) pos[i] = S.insert(pos[i - 1], s[i] - 'a');
for ( int i = 1; i <= S.tot; i ++) G[S.link[i]].push_back(i);
for ( int i = 1; i <= n; i ++) siz[pos[i]] = 1;
dfs(0);
cout << ans << '\n';
return 0;
}
不同子串个数
求不同子串个数,有两种解法。
第一种,SAM 上从 \(P\) 开始走的每一条不同路径都代表一个子串,那么就是 SAM 上对路径数计数,这个直接在 SAM 上 dp 即可。
第二种,SAM 上每个节点都是一个等价类,那么可以统计每个等价类中字符串的个数再求和,一个等价类 \(E\) 的字符串个数是 \(len(E)-minlen(E)+1\),也就等于 \(len(E)-len(link(E))\)。对这个求和即可。
我写的第二种。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 2e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
struct SAM {
int tot;
int link[N], len[N];
int ch[26][N];
void init() {
for ( int i = 0; i <= tot; i ++) {
link[i] = len[i] = 0;
for ( int j = 0; j < 26; j ++)
ch[j][i] = 0;
}
tot = 0, link[0] = -1;
}
int insert( int lst, int c) {
int cur = ++ tot, p = lst, q, clone;
len[cur] = len[p] + 1;
while (p != -1 && ! ch[c][p]) ch[c][p] = cur, p = link[p];
if (p == -1) return link[cur] = 0, cur;
if (len[p] + 1 == len[q = ch[c][p]]) return link[cur] = q, cur;
clone = ++ tot, len[clone] = len[p] + 1;
link[clone] = link[q];
for ( int i = 0; i < 26; i ++) ch[i][clone] = ch[i][q];
while (p != -1 && ch[c][p] == q) ch[c][p] = clone, p = link[p];
link[cur] = link[q] = clone;
return cur;
}
} S;
int n;
char s[N];
int pos[N];
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n;
cin >> (s + 1);
S.init();
for ( int i = 1; i <= n; i ++) pos[i] = S.insert(pos[i - 1], s[i] - 'a');
long long ans = 0;
for ( int i = 1; i <= S.tot; i ++) ans += S.len[i] - S.len[S.link[i]];
cout << ans << '\n';
return 0;
}
【模板】广义后缀自动机(广义 SAM)
现在要对很对个串求不同的子串个数。
建立广义后缀自动机有很多假做法,所以这个题还要输出建立的广义 SAM 的点数,需要满足这个点数最小。
仿照 AC 自动机的方式,考虑把这些串插入到 Trie 上,然后在 Trie 上 bfs,建立 SAM。
其实很简单,数组 \(pos_i\) 的定义改一下,表示建立了 Trie 上节点 \(i\) 所对应的字符串时,SAM 上的节点编号。
求不同子串个数就直接算即可。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 2e6 + 10, M = 1e6 + 10, inf = 1e9, mod = 998244353;
int n;
int pos[M];
struct Trie {
int tot;
int ch[26][M];
void init() {
for ( int i = 0; i <= tot; i ++)
for ( int j = 0; j < 26; j ++)
ch[j][i] = 0;
tot = 0;
}
void insert( char s[]) {
int n = strlen(s + 1), u = 0;
for ( int i = 1; i <= n; i ++) {
int & v = ch[s[i] - 'a'][u];
if (! v) v = ++ tot;
u = v;
}
}
} T;
struct SAM {
int tot;
int link[N], len[N];
int ch[26][N];
void init() {
for ( int i = 0; i <= tot; i ++) {
link[i] = len[i] = 0;
for ( int j = 0; j < 26; j ++)
ch[j][i] = 0;
}
tot = 0, link[0] = -1;
}
int insert( int lst, int c) {
int cur = ++ tot, p = lst, q, clone;
len[cur] = len[p] + 1;
while (p != -1 && ! ch[c][p]) ch[c][p] = cur, p = link[p];
if (p == -1) return link[cur] = 0, cur;
if (len[p] + 1 == len[q = ch[c][p]]) return link[cur] = q, cur;
clone = ++ tot, len[clone] = len[p] + 1;
link[clone] = link[q];
for ( int i = 0; i < 26; i ++) ch[i][clone] = ch[i][q];
while (p != -1 && ch[c][p] == q) ch[c][p] = clone, p = link[p];
link[cur] = link[q] = clone;
return cur;
}
} S;
void build() {
queue< int> q;
for ( int i = 0, u; i < 26; i ++)
if (u = T.ch[i][0]) pos[u] = S.insert(pos[0], i), q.push(u);
while (q.size()) {
int u = q.front(); q.pop();
for ( int i = 0, v; i < 26; i ++)
if (v = T.ch[i][u]) {
pos[v] = S.insert(pos[u], i);
q.push(v);
}
}
}
char s[N];
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n;
T.init(), S.init();
while (n --) {
cin >> (s + 1);
T.insert(s);
}
build();
long long ans = 0;
for ( int i = 1; i <= S.tot; i ++) ans += S.len[i] - S.len[S.link[i]];
cout << ans << '\n' << S.tot + 1 << '\n';
return 0;
}
【模板】AC 自动机
求每个模板串出现的次数。
可以对文本串建立 SAM,那么每个模板串其实都是文本串的子串。(不是子串就输出 \(0\))
直接在 SAM 上求子串出现次数即可。
但是这个题卡空间,这个没办法,本来就不是 SAM 做的。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 4e6 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
struct SAM {
int tot;
int link[N], len[N];
int ch[26][N];
void init() {
for ( int i = 0; i <= tot; i ++) {
link[i] = len[i] = 0;
for ( int j = 0; j < 26; j ++)
ch[j][i] = 0;
}
tot = 0, link[0] = -1;
}
int insert( int lst, int c) {
int cur = ++ tot, p = lst, q, clone;
len[cur] = len[p] + 1;
while (p != -1 && ! ch[c][p]) ch[c][p] = cur, p = link[p];
if (p == -1) return link[cur] = 0, cur;
if (len[p] + 1 == len[q = ch[c][p]]) return link[cur] = q, cur;
clone = ++ tot, len[clone] = len[p] + 1;
link[clone] = link[q];
for ( int i = 0; i < 26; i ++) ch[i][clone] = ch[i][q];
while (p != -1 && ch[c][p] == q) ch[c][p] = clone, p = link[p];
link[cur] = link[q] = clone;
return cur;
}
} S;
int n;
int pos[N], siz[N];
vector < int> G[N];
string t[N];
string s;
void dfs( int u) {
for ( auto v : G[u]) dfs(v), siz[u] += siz[v];
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n;
for ( int i = 1; i <= n; i ++) {
cin >> t[i];
t[i] = ' ' + t[i];
}
cin >> s, s = ' ' + s;
S.init();
for ( int i = 1; i < (int)s.size(); i ++)
pos[i] = S.insert(pos[i - 1], s[i] - 'a');
for ( int i = 1; i <= S.tot; i ++) G[S.link[i]].push_back(i);
for ( int i = 1; i < (int)s.size(); i ++) siz[pos[i]] = 1;
dfs(0);
for ( int o = 1; o <= n; o ++) {
int u = 0, F = 1;
for ( int i = 1; i < (int)t[o].size(); i ++) {
if (S.ch[t[o][i] - 'a'][u]) u = S.ch[t[o][i] - 'a'][u];
else {
F = 0;
break ;
}
}
if (! F) cout << "0\n";
else cout << siz[u] << '\n';
}
return 0;
}
【模板】后缀排序
要求对每个后缀排序,但是 SAM 上的节点对应一个前缀啊。
那么考虑对串 \(S\) 建立反串,记反串为 \(T\),对反串 \(T\) 建 SAM。
在 parent 树上看,某些节点就对应 \(T\) 的一个前缀,也就是 \(S\) 的后缀的反串,所以要维护节点对应的字符串的反串的字典序。
可以知道,一个点 \(u\) 的 \(link(u)\) 代表的字符串是 \(u\) 的后缀,那么对于 \(link(u)\) 的所有儿子节点,决定它们反串的字典序的是下图 \(a\) 字符的大小。
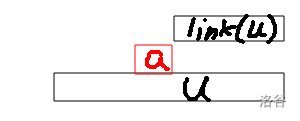
那么只要能求出这个 \(a\) 字符,在 parent 树上按照 \(a\) 字符的字典序进行搜索,先遍历到的叶子节点字典序就更小。
求 \(a\) 字符可以用这个点对应的字符串 \(T\) 上的位置减去它父亲的 \(len\),记这个值为 \(i\),那么 \(T_i\) 也就是这个字符,在 \(S\) 上就是 \(S_{n-i+1}\) 为这个字符。
求出来后,按照这个字符大小从小到大给边排序,然后搜索即可,复杂度 \(O(n\log n)\)。
当然,SAM 还是会被卡空间,因为这个题的字符集大小有 \(60\)。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 1e6 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
struct SAM {
int tot;
int link[N * 2], len[N * 2], pos[N * 2], rev[N * 2];
map< char, int> ch[N * 2];
void init() {
for ( int i = 0; i <= tot; i ++) {
link[i] = len[i] = pos[i] = rev[i] = 0;
ch[i].clear();
}
tot = 0, link[0] = -1;
}
int insert( int lst, char c, int id) {
int cur = ++ tot, p = lst, q, clone;
pos[cur] = len[cur] = len[p] + 1, rev[cur] = id;
// pos[cur] 代表 cur 对应的字符串在 T 的位置
// res[cur] 代表 cur 对应的字符串在 S 的位置
while (p != -1 && ! ch[p][c]) ch[p][c] = cur, p = link[p];
if (p == -1) return link[cur] = 0, cur;
if (len[p] + 1 == len[q = ch[p][c]]) return link[cur] = q, cur;
clone = ++ tot, len[clone] = len[p] + 1;
link[clone] = link[q], pos[clone] = pos[q];
ch[clone] = ch[q];
while (p != -1 && ch[p][c] == q) ch[p][c] = clone, p = link[p];
link[cur] = link[q] = clone;
return cur;
}
} S;
char s[N];
int pos[N], n;
char to[N * 2];
vector< int> G[N * 2];
void dfs( int u) {
if (S.rev[u]) cout << S.rev[u] << ' ';
for ( auto v : G[u]) dfs(v);
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> (s + 1);
n = strlen(s + 1);
S.init();
for ( int i = n; i; i --) pos[n - i + 1] = S.insert(pos[n - i], s[i], i);
for ( int i = 1; i <= S.tot; i ++)
to[i] = s[n + 1 - S.pos[i] + S.len[S.link[i]]],
G[S.link[i]].push_back(i);
for ( int i = 0; i <= S.tot; i ++)
sort(G[i].begin(), G[i].end(), [&]( int a, int b) {
return to[a] < to[b];
});
dfs(0);
return 0;
}
树上后缀排序
想了很久,结果是题读错了。
最开始以为是从根到点构成的字符串进行排序,这样不建反串做不了,但是树上又不能建反串。
然后发现其实是点到根构成的字符串进行排序,那么就可以直接建 SAM 做了。
和上面那道题的做法其实一样,在树上直接建广义 SAM 即可。
求 \(a\) 字符时,其实就是树上 \(k\) 级祖先,从节点 \(u\) 在树上对应的点往上跳 \(len(link(u))\) 次即可。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 1e6 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
struct SAM {
int tot;
int link[N], len[N], pos[N], rev[N];
int ch[26][N];
void init() {
for ( int i = 0; i <= tot; i ++) {
link[i] = len[i] = pos[i] = rev[i] = 0;
for ( int j = 0; j < 26; j ++)
ch[j][i] = 0;
}
tot = 0, link[0] = -1;
}
int insert( int lst, int c, int id) {
int cur = ++ tot, p = lst, q, clone;
len[cur] = len[p] + 1, pos[cur] = rev[cur] = id;
// pos[cur] 代表节点 cur 在树上对应的点的编号
// pos 和 rev 的区别是:对于复制节点 clone,pos 仍然有效;rev 只对除复制节点以外的节点有效
while (p != -1 && ! ch[c][p]) ch[c][p] = cur, p = link[p];
if (p == -1) return link[cur] = 0, cur;
if (len[p] + 1 == len[q = ch[c][p]]) return link[cur] = q, cur;
clone = ++ tot, len[clone] = len[p] + 1;
link[clone] = link[q], pos[clone] = pos[q];
for ( int i = 0; i < 26; i ++) ch[i][clone] = ch[i][q];
while (p != -1 && ch[c][p] == q) ch[c][p] = clone, p = link[p];
link[cur] = link[q] = clone;
return cur;
}
} S;
int n;
int fa[N], pos[N];
vector< int> G[N], E[N];
char s[N], to[N];
int siz[N], son[N], dep[N];
void dfs( int u) {
pos[u] = S.insert(pos[fa[u]], s[u] - 'a', u);
siz[u] = 1, dep[u] = dep[fa[u]] + 1;
for ( auto v : G[u])
dfs(v),
siz[u] += siz[v],
son[u] = (siz[v] > siz[son[u]] ? v : son[u]);
}
int top[N], dfn[N], rev[N], tot;
void dfs2( int u, int topt) {
top[u] = topt, dfn[u] = ++ tot, rev[tot] = u;
if (son[u]) dfs2(son[u], topt);
for ( auto v : G[u])
if (v != son[u]) dfs2(v, v);
}
int Kth( int u, int k) {
while (dep[u] - dep[top[u]] + 1 <= k) {
k -= (dep[u] - dep[top[u]] + 1);
u = fa[top[u]];
}
return rev[dfn[u] - k];
}
// 树上 k 级祖先
void Dfs( int u) {
if (S.rev[u]) cout << S.rev[u] << ' ';
for ( auto v : E[u]) Dfs(v);
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n;
S.init();
for ( int i = 2; i <= n; i ++) cin >> fa[i], G[fa[i]].push_back(i);
cin >> (s + 1);
dfs(1), dfs2(1, 1);
for ( int i = 1; i <= S.tot; i ++)
to[i] = s[Kth(S.pos[i], S.len[S.link[i]])],
E[S.link[i]].push_back(i);
for ( int i = 0; i <= S.tot; i ++)
sort(E[i].begin(), E[i].end(), [&]( int a, int b) {
return to[a] == to[b] ? a < b : to[a] < to[b];
});
Dfs(0);
return 0;
}
[TJOI2015] 弦论
求第 \(k\) 小子串,但题目给了两种情况,要对两种情况分别求解。
第一种:不同位置相同子串算作一个,也就是把本质不同的子串列出来,求第 \(k\) 小的。
思路很明显,首先 SAM 上从 \(P\) 出发经过的每一个路径都对应一个子串,且没有重复的,所以考虑对每个节点算一个 \(f\),\(f_u\) 就表示从 \(u\) 出发的路径个数,这个在 SAM 上转移即可。
然后在 SAM 上走,当前节点为 \(u\),按边的字典序枚举下一个点 \(v\),如果 \(v\) 满足 \(f_v+1\ge k\)(\(+1\) 是要算上 \(u\to v\) 这条路径),说明第 \(k\) 小子串在从 \(v\) 开始的路径中,就走向 \(v\),然后将 \(k-1\);否则说明第 \(k\) 小子串不在从 \(v\) 开始的路径中,那么在枚举的下一个点 \(v'\) 中看有没有第 \(k-(f_v+1)\) 小的子串,继续做即可,直到 \(k=0\)。
第二种:不同位置相同子串算作多个,那么先在 SAM 上把每个子串出现的次数求出来,设节点 \(u\) 的子串个数为 \(siz_u\),那么 \(f_u\) 也就是带了个 \(siz\) 的权,剩下的做法和上述一样。
代码
#include <bits/stdc++.h>
#define ll long long
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 1e6 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
struct SAM {
int tot;
int link[N], len[N];
int ch[26][N];
void init() {
for ( int i = 0; i <= tot; i ++) {
link[i] = len[i] = 0;
for ( int j = 0; j < 26; j ++)
ch[j][i] = 0;
}
tot = 0, link[0] = -1;
}
int insert( int lst, int c) {
int cur = ++ tot, p = lst, q, clone;
len[cur] = len[p] + 1;
while (p != -1 && ! ch[c][p]) ch[c][p] = cur, p = link[p];
if (p == -1) return link[cur] = 0, cur;
if (len[p] + 1 == len[q = ch[c][p]]) return link[cur] = q, cur;
clone = ++ tot, len[clone] = len[p] + 1;
link[clone] = link[q];
for ( int i = 0; i < 26; i ++) ch[i][clone] = ch[i][q];
while (p != -1 && ch[c][p] == q) ch[c][p] = clone, p = link[p];
link[cur] = link[q] = clone;
return cur;
}
} S;
int n, op, k;
int pos[N], siz[N], vis[N];
char s[N];
vector< int> G[N];
void dfs( int u) {
for ( auto v : G[u])
dfs(v), siz[u] += siz[v];
}
ll f[N];
void Dfs( int u) {
if (vis[u]) return ;
vis[u] = 1;
for ( int i = 0; i < 26; i ++) {
int v = S.ch[i][u];
if (! v) continue ;
Dfs(v);
int t = op ? siz[v] : 1;
f[u] += t + f[v];
}
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
S.init();
cin >> (s + 1);
n = strlen(s + 1);
for ( int i = 1; i <= n; i ++) pos[i] = S.insert(pos[i - 1], s[i] - 'a'), siz[pos[i]] = 1;
for ( int i = 1; i <= S.tot; i ++) G[S.link[i]].push_back(i);
cin >> op >> k;
dfs(0), Dfs(0);
int u = 0;
if (f[u] < k) return cout << "-1\n", 0;
while (k > 0) {
for ( int i = 0; i < 26; i ++) {
int v = S.ch[i][u];
if (! v) continue ;
int t = op ? siz[v] : 1;
if (f[v] + t >= k) {
u = v, cout << char(i + 'a'), k -= t;
break ;
} else k -= (f[v] + t);
}
}
return 0;
}
[JSOI2007] 字符加密
把所有字符串列出来排序,这个操作很像后缀排序,但还是有点区别。
可以想到把字符串复制一遍接在后面,这样就变成了后缀排序,直接 SAM 维护即可。
这个题字符集有点大,所以可以用 map 来存边。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 4e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
char s[N];
struct SAM {
int tot;
int link[N], len[N], pos[N], rev[N];
map< char, int> ch[N];
void init() {
for ( int i = 0; i <= tot; i ++) {
link[i] = len[i] = pos[i] = rev[i] = 0;
ch[i].clear();
}
tot = 0, link[0] = -1;
}
int insert( int lst, char c, int id) {
int cur = ++ tot, p = lst, q, clone;
pos[cur] = len[cur] = len[p] + 1, rev[cur] = id;
while (p != -1 && ! ch[p].count(c)) ch[p][c] = cur, p = link[p];
if (p == -1) return link[cur] = 0, cur;
if (len[p] + 1 == len[q = ch[p][c]]) return link[cur] = q, cur;
clone = ++ tot, len[clone] = len[p] + 1;
link[clone] = link[q], pos[clone] = pos[q];
ch[clone] = ch[q];
while (p != -1 && ch[p][c] == q) ch[p][c] = clone, p = link[p];
link[cur] = link[q] = clone;
return cur;
}
} S;
int n;
int pos[N];
char to[N];
vector< int> G[N];
void dfs( int u) {
if (S.rev[u] && S.rev[u] <= n) cout << s[S.rev[u] + n - 1];
for ( auto v : G[u]) dfs(v);
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> (s + 1);
n = strlen(s + 1);
S.init();
for ( int i = 1; i <= n; i ++) s[i + n] = s[i];
for ( int i = n * 2; i; i --) pos[n * 2 - i + 1] = S.insert(pos[n * 2 - i], s[i], i);
for ( int i = 1; i <= S.tot; i ++)
to[i] = s[2 * n + 1 - S.pos[i] + S.len[S.link[i]]],
G[S.link[i]].push_back(i);
for ( int i = 0; i <= S.tot; i ++)
sort(G[i].begin(), G[i].end(), [&]( int a, int b) {
return to[a] < to[b];
});
dfs(0);
return 0;
}
[AHOI2013] 差异
考虑建反串的 SAM,刚好两个节点在 parent 树上的 \(\rm{lca}\) 就是原串中这两个串的 \(\rm{lcp}\)。
那么那个式子的计算就很简单了,考虑把 \(len(T_i)\) 的贡献和 \(2\times len(\rm{lcp})\) 的贡献拆开。
显然,每个 \(len(T_i)\) 会被加 \(n-1\) 次,那么就只用考虑 \(2\times len(\rm{lcp})\) 会被计算多少次。
单独对每个 parent 树上每个节点计算当它为 \(\rm{lcp}\) 时的贡献。
那么主要就是计算这个点会成为多少次 \(\rm{lcp}\),计算这个很简单,随便算算即可。
代码
#include <bits/stdc++.h>
#define ll long long
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 1e6 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
struct SAM {
int tot;
int link[N], len[N];
int ch[26][N];
void init() {
for ( int i = 0; i <= tot; i ++) {
link[i] = len[i] = 0;
for ( int j = 0; j < 26; j ++)
ch[j][i] = 0;
}
tot = 0, link[0] = -1;
}
int insert( int lst, int c) {
int cur = ++ tot, p = lst, q, clone;
len[cur] = len[p] + 1;
lst = cur;
while (p != -1 && ! ch[c][p]) ch[c][p] = cur, p = link[p];
if (p == -1) return link[cur] = 0, cur;
if (len[p] + 1 == len[q = ch[c][p]]) return link[cur] = q, cur;
clone = ++ tot, len[clone] = len[p] + 1;
link[clone] = link[q];
for ( int i = 0; i < 26; i ++) ch[i][clone] = ch[i][q];
while (p != -1 && ch[c][p] == q) ch[c][p] = clone, p = link[p];
link[cur] = link[q] = clone;
return cur;
}
} S;
int n;
int pos[N], siz[N];
char s[N];
ll ans;
vector< int> G[N];
void dfs( int u) {
for ( auto v : G[u])
dfs(v), siz[u] += siz[v];
int sum = siz[u];
ll cnt = 0;
for ( auto v : G[u])
sum -= siz[v], cnt += 1ll * siz[v] * sum;
ans -= cnt * 2 * S.len[u];
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> (s + 1);
n = strlen(s + 1);
S.init();
for ( int i = n; i; i --) pos[n - i + 1] = S.insert(pos[n - i], s[i] - 'a');
for ( int i = 1; i <= n; i ++) ans += 1ll * S.len[pos[i]] * (n - 1), siz[pos[i]] = 1;
for ( int i = 1; i <= S.tot; i ++) G[S.link[i]].push_back(i);
dfs(0);
cout << ans << '\n';
return 0;
}
[SDOI2016] 生成魔咒
这个题要动态求子串个数,每次插入一个字符后,给答案加上 \(len(pos_i)-len(link(pos_i))\),也就是节点 \(pos_i\) 的等价类中的字符串个数即可。
这里一个容易产生疑惑的地方,就为什么建完串后求子串个数就要枚举所有 SAM 上的点(包括复制点),而动态插入时就只用加上 \(pos_i\) 的?
其实是因为 SAM 的形态会随着加点而变化,假设现在插入点 \(u\),SAM 里面可能会新建出 \(clone\) 节点,假设 \(clone\) 节点复制的是 \(v\) 节点,就算 \(v\) 节点信息后续被改动,但统计 \(v\) 的贡献的时候信息是没被改动的,也就是说统计 \(v\) 贡献时的 \(v\) 是包含了 \(clone\) 的所有信息的,所以统计了 \(v\) 就不需要统计 \(clone\)。
而如果将 SAM 全部建完再计算子串个数,肯定就需要对所有节点统计贡献了,因为现在 SAM 中每个节点存的信息都是最终形态。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 2e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
struct SAM {
int tot;
int link[N], len[N];
map< int, int> ch[N];
void init() {
for ( int i = 0; i <= tot; i ++) {
link[i] = len[i] = 0;
ch[i].clear();
}
tot = 0, link[0] = -1;
}
int insert( int lst, int c) {
int cur = ++ tot, p = lst, q, clone;
len[cur] = len[p] + 1;
lst = cur;
while (p != -1 && ! ch[p].count(c)) ch[p][c] = cur, p = link[p];
if (p == -1) return link[cur] = 0, cur;
if (len[p] + 1 == len[q = ch[p][c]]) return link[cur] = q, cur;
clone = ++ tot, len[clone] = len[p] + 1;
link[clone] = link[q];
ch[clone] = ch[q];
while (p != -1 && ch[p][c] == q) ch[p][c] = clone, p = link[p];
link[cur] = link[q] = clone;
return cur;
}
} S;
int n;
int pos[N];
long long ans;
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n;
S.init();
for ( int i = 1; i <= n; i ++) {
int x; cin >> x;
pos[i] = S.insert(pos[i - 1], x);
ans += S.len[pos[i]] - S.len[S.link[pos[i]]];
cout << ans << '\n';
}
return 0;
}
[NOI2015] 品酒大会
考虑怎么刻画这个 \(r\) 相似,也就是两个后缀串的 \(\rm{lcp}\) 的长度是否大于等于 \(r\),那么按照惯例,对 \(S\) 建立反串,这样树上 \(\rm{lca}\) 就是原串的 \(\rm{lcp}\)。
问题可以转化到树上了,首先考虑第一个问,\(r\) 相似的个数,那么枚举每个 \(\rm{lca}\),那么也就是求它子树中选两个点使得它为 \(\rm{lca}\) 的方案数记为 \(w\),那么就给 \(1\sim len(\rm{lca})\) 的 \(r\) 都加上 \(w\)。
现在考虑第二个问,还要求对应权值相乘的最大值,对子树维护最大、次大、最小、次小,然后取最大乘次大、最小乘次小的最大值即可。
最后对 \(r=0\) 的单独计算答案即可。
代码
#include <bits/stdc++.h>
#define ll long long
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 6e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
struct SAM {
int link[N], len[N];
int ch[26][N];
int tot = 0;
void init() {
for ( int i = 0; i <= tot; i ++) {
link[i] = len[i] = 0;
for ( int j = 0; j < 26; j ++) ch[j][i] = 0;
}
tot = 0, link[0] = -1;
}
int insert( int lst, int c) {
int cur = ++ tot, p = lst, q, clone;
len[cur] = len[p] + 1;
while (p != -1 && ! ch[c][p]) ch[c][p] = cur, p = link[p];
if (p == -1) return link[cur] = 0, cur;
if (len[p] + 1 == len[q = ch[c][p]]) return link[cur] = q, cur;
clone = ++ tot;
len[clone] = len[p] + 1, link[clone] = link[q];
for ( int i = 0; i < 26; i ++) ch[i][clone] = ch[i][q];
while (p != -1 && ch[c][p] == q) ch[c][p] = clone, p = link[p];
link[cur] = link[q] = clone;
return cur;
}
} S;
int pos[N], siz[N];
vector< int> G[N];
int n;
char s[N];
int a[N];
ll Cnt[N];
int Mi[N], Mii[N], Mx[N], Mxx[N];
ll MAX[N];
void dfs( int u) {
for ( auto v : G[u]) {
dfs(v);
siz[u] += siz[v];
if (Mx[v] >= Mx[u]) Mxx[u] = Mx[u], Mx[u] = Mx[v];
else if (Mx[v] > Mxx[u]) Mxx[u] = Mx[v];
if (Mi[v] <= Mi[u]) Mii[u] = Mi[u], Mi[u] = Mi[v];
else if (Mi[v] < Mii[u]) Mii[u] = Mi[v];
}
int sum = siz[u];
ll cnt = 0;
for ( auto v : G[u])
sum -= siz[v], cnt += 1ll * siz[v] * sum;
if (Mx[u] > -inf && Mxx[u] > -inf) MAX[S.len[u]] = max(MAX[S.len[u]], 1ll * Mx[u] * Mxx[u]);
if (Mi[u] < inf && Mii[u] < inf) MAX[S.len[u]] = max(MAX[S.len[u]], 1ll * Mi[u] * Mii[u]);
Cnt[S.len[u]] += cnt;
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n;
cin >> (s + 1);
memset(MAX, 128, sizeof MAX);
memset(Mx, 128, sizeof Mx), memset(Mxx, 128, sizeof Mxx);
memset(Mi, 127, sizeof Mi), memset(Mii, 127, sizeof Mii);
int mx = -inf, mxx = -inf, mi = inf, mii = inf;
for ( int i = 1; i <= n; i ++) {
cin >> a[i];
if (a[i] >= mx) mxx = mx, mx = a[i];
else if (a[i] > mxx) mxx = a[i];
if (a[i] <= mi) mii = mi, mi = a[i];
else if (a[i] < mii) mii = a[i];
}
cout << 1ll * n * (n - 1) / 2 << ' ' << max(1ll * mx * mxx, 1ll * mi * mii) << '\n';
S.init();
for ( int i = n; i; i --) pos[i] = S.insert(pos[i + 1], s[i] - 'a');
for ( int i = 1; i <= S.tot; i ++) G[S.link[i]].push_back(i);
for ( int i = 1; i <= n; i ++) siz[pos[i]] = 1, Mx[pos[i]] = Mi[pos[i]] = a[i];
dfs(0);
for ( int i = n - 1; i; i --) Cnt[i] += Cnt[i + 1], MAX[i] = max(MAX[i], MAX[i + 1]);
for ( int i = 1; i < n; i ++) {
cout << Cnt[i] << ' ';
if (Cnt[i]) cout << MAX[i] << '\n';
else cout << "0\n";
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号