三个顶点均在椭圆上的三角形称为椭圆的内接三角形,已知点\(A\)是椭圆的一个短轴端点,如果以\(A\)为直角顶点的椭圆内接等腰直角三角形有且仅有三个,则椭圆的离心率的取值范围是\(\underline{\qquad\qquad}\).
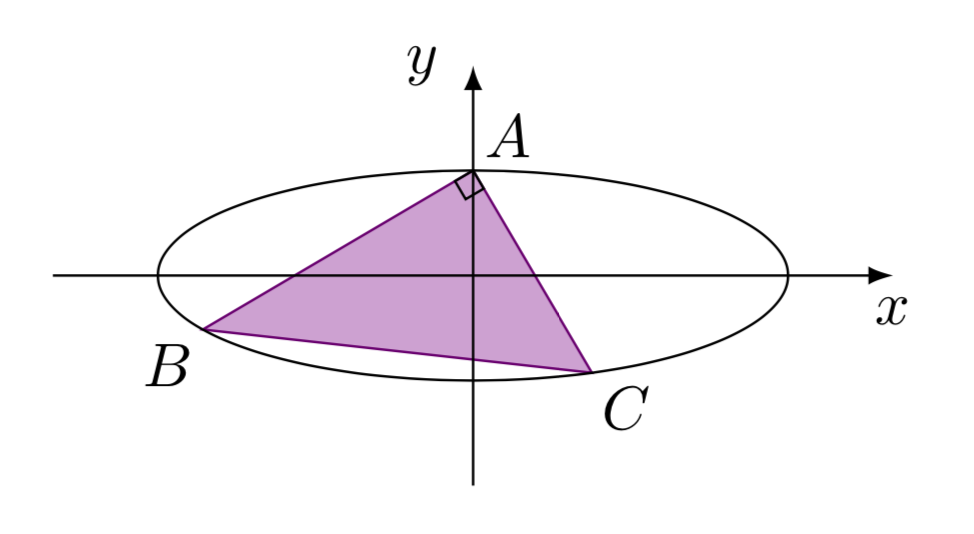
解析: \(\triangle ABC\)与椭圆如图所示,不妨设椭圆方程为$$
\dfrac{x2}{a2}+\dfrac{y2}{b2}=1,a>b>0.$$
因此原椭圆在新坐标系下的直角坐标方程为$$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{2y}{b}=0.\qquad (\ast)$$建立以新坐标系坐标原点$O$为极点,以新坐标系的$x$轴的正半轴为极轴的极坐标系,设$$\angle CAx=\theta,\theta\in\left(0,\dfrac{\pi}{2}\right).$$则$C,B$点的极坐标可设为$$C\left(\rho_1,2\pi-\theta\right),B\left(\rho_2,2\pi-\theta-\dfrac{\pi}{2}\right),$$则$C$的直角坐标可表示为$$C\left(\rho_1 \cos\theta,-\rho_1 \sin\theta\right),B\left(-\rho_2 \sin\theta,-\rho_2 \cos\theta\right)$$将$C,B$两点坐标分别代入方程$(\ast)$,并整理可得$$ \rho_1=\dfrac{\dfrac{2\sin\theta}{b}}{\dfrac{\cos^2\theta}{a^2}+\dfrac{\sin^2\theta}{b^2}},\rho_2=\dfrac{\dfrac{2\cos\theta}{b}}{\dfrac{\sin^2\theta}{a^2}+\dfrac{\cos^2\theta}{b^2}}.$$结合$\rho_1=\rho_2$可得关于$\theta$的方程$$ \dfrac{b^2}{a^2}\tan^3\theta-\tan^2\theta+\tan\theta-\dfrac{b^2}{a^2}=0,\theta\in\left(0,\dfrac{\pi}{2}\right).$$ 题意即关于$\tan\theta$的方程有三个解,易求得$\dfrac{b^2}{a^2}$的取值范围为$\left(0,\dfrac{1}{3}\right)$,因此所求离心率的取值范围为$\left(\dfrac{\sqrt{6}}{3},1\right)$.