我怎么进的集训队

Petrozavodsk Winter 2021. Day 6. PKU Contest 2

简单 Round。

A. Best Subsequence

设 \(f(L,R,k,W)\) 表示，区间 \([L,R]\) 中能否选出一个长度为 \(k\) 的子序列，使得任意两项的和 \(\le W\)。\(f\) 关于 \(k\) 和 \(W\) 都有单调性，我们可以二分 \(W\)，计算最大的 \(k_0\)，判断是否有 \(k \le k_0\)。

记 \(\le \frac{W}{2}\) 的为一类下标，\(> \frac{W}{2}\) 的为二类下标。显然二类下标不能环相邻。如果有一个一类下标不在最优的子序列中，我们可以将其加入，代价是至多删掉一个二类下标，不会更劣，因此我们可以将所有的一类下标先加入最优子序列中。

如果两个相邻的一类下标分别是 \(i_1\) 和 \(i_2\)，如果 \(W \ge \max(a_{i_1},a_{i_2}) + \min_{i_1 < j < i_2} a_j\)，那么可以多加入一个二类下标。

那么一对相邻下标（原序列上的）会给一个区间内的 \(W\) 带来 \(k_0 \leftarrow k_0+1\) 的贡献，另一个区间的 \(W\) 额外带来 \(k_0 \leftarrow k_0+1\) 的贡献。使用主席树维护即可。

B. Binary Search Tree

我竟然没做出来，还好我已经退役了。

首先考虑换维：对序列扫描线，尝试维护每一个时刻的信息。

我自己想的是，维护一个序列，有值的位置表示这个时刻（后面会看到他的麻烦之处）。你需要处理的是：位置 \(q\) 之前，所有 \(\le w\) 的数构成的序列的前缀 \(\max\) 之和，以及位置 \(q\) 之前，所有 \(\ge w\) 的数构成的序列的前缀 \(\min\) 之和。

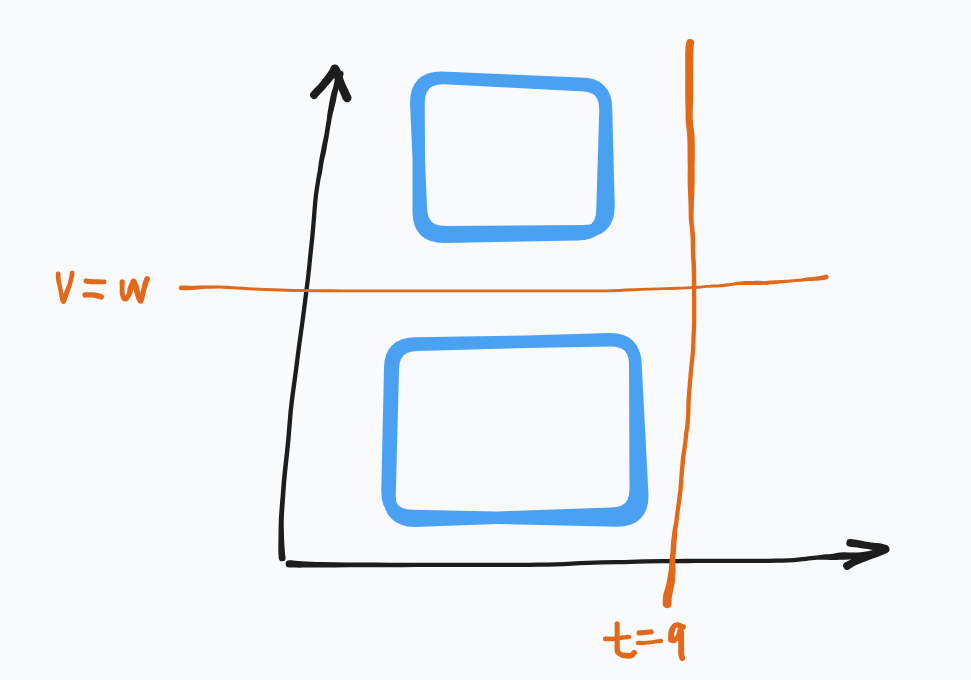
大概可以感受一下，在序列上维护“值分割”是非常难的，所以在这个方向上再次换维，发现可以线段树二分 + 线段树单侧递归实现。

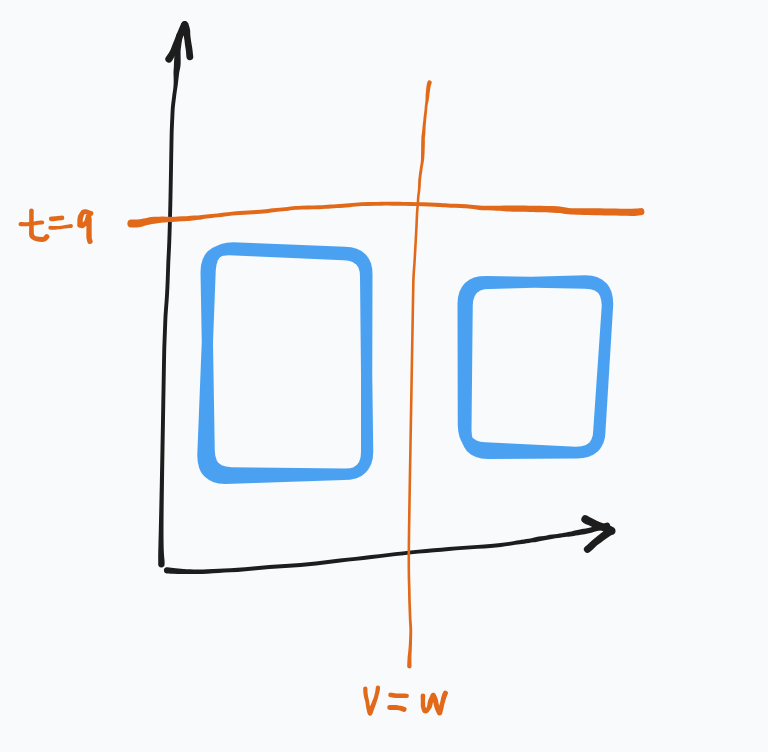
C. Circle

计算几何。给定一个圆，做出这样的图形：

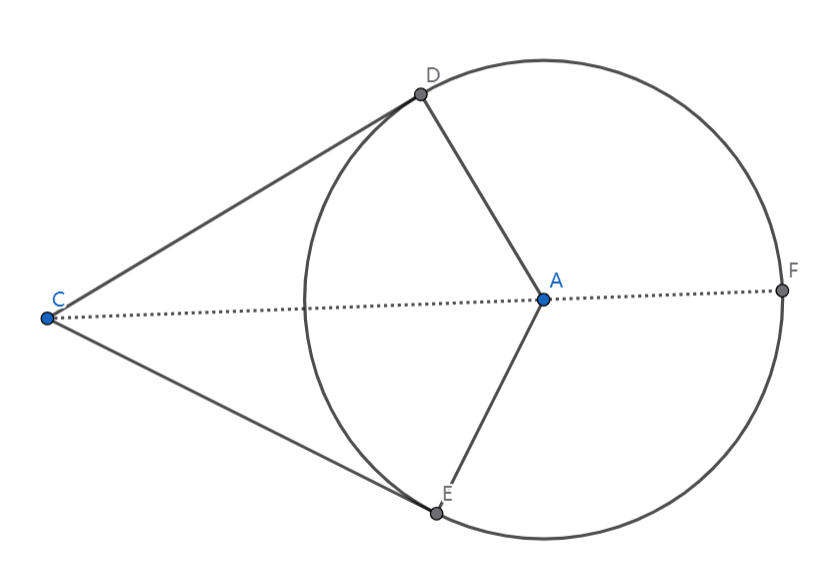
发现 \(P : F \to D \to E\) 这一段上，\(C \to P\) 的距离（非直线）最小距离是一个凸函数（具体而言是直线拼上一段凸的曲线，可以自行脑补）。

如果是凸的，可以直接三分，但是有一些断点，还是比较麻烦的。一个最暴力的想法是，我们将圆周划分为至多 \(3\) 个区间，每个区间内两个距离都是凸的，那么和也是凸的，直接三分。

然后就是如何计算一个点到圆上一点的最短距离了。不用求解切点，我们用极角处理一切！常数很大，尽可能减少三角函数与反三角函数的调用。

D. Composite Sequence

当 \(n\) 大于某个很小的常数时，一定有解。剩下的暴力即可。

E. Four XOR

考虑所有的 \(1 \le i < j \le n\)，\(a_i \oplus a_j\) 最多 \(2V\) 种可能，那么存在一个 \(k\) 使得至少有 \(\lceil \frac{n(n-1)}{4V} \rceil\) 个 \((i,j)\) 使得 \(a_i \oplus a_j = k\)。

有解等价于存在 \((i_1,j_1)\) 和 \((i_2,j_2)\) 使得 \(\{i_1,j_1\} \cap \{i_2,j_2\} = \varnothing\)。我们猜一猜，如果同一个 \(k\) 对应的 \((i,j)\) 比较多，那么一定有解。

如果无解，则任意两对数，都有公共元素。实际上这是一个非常严格的要求，只能是两种之一：

1. 三对元素，分别是 \((a,b),(a,c),(b,c)\)；
2. 存在一个元素，使得他在所有元素对中出现。

分析第二种情况，如果元素对超过 \(4\)，那么说明至少有 \(4\) 个数完全相同，他们异或起来恰好为 \(0\)。

因此无解的必要条件是 \(\lceil \frac{n(n-1)}{4V} \rceil \le 3\)，这样 \(n \le O(\sqrt V)\)。所以 \(n\) 小的时候暴力，\(n\) 大的时候直接输出 YES 即可。

F. Game

非常有趣的题目！记 \(dp_i\) 为当前在 \(i\) 能获得的最大收益，则 \(dp_{i} = \max\{a_i,\frac{dp_{i-1}+dp_{i+1}}{2}\}\)，发现 \(dp_i\) 是确定的，你的决策也应该是确定的、只和 \(i\) 有关的。

那么假设我们选定了 \(1 = p_1 < p_2 < \cdots < p_k = n\)，那么此时答案为：

\[\frac{1}{2n}(\sum_{i=1}^k 2a_{p_i} + \sum_{i=1}^{k-1} (p_{i+1}-p_i-1)(a_{p_i}+a_{p_{i+1}}) \]

将这个式子减去 \(a_1+a_n\) 后，你惊奇的发现：总和乘上 \(n\)，是 \((p_i,a_{p_i})\) 构成的曲边梯形的面积。我们要最大化梯形的面积——不就是求出凸包吗！所以本题可以 \(O(n)\) 求解。

G. GPA

当前的状态显然只有：Alice 不高兴的次数，以及之前比赛成绩总和。

而 Alice 不高兴次数固定的时候，之前比赛的成绩总和越小越好，所以可以将其放到 DP 数组里面，复杂度平方。

H. Local Maxima

有趣的计数题！我提供一个并不需要容斥的做法。

考虑从高到低往方格表中填数，维护集合 \(S\) 表示：当前有数的行和列构成的集合。每次填入一个方格，其行或列至少有一个在 \(S\) 中，并且有可能在 \(S\) 中增加元素。

正着做太困难了，维护的信息不可能低于四次方，那么考虑把整个过程反过来！每次选出一个行或者列，表示最后一次加入 \(S\) 的是这一行或列。我们枚举这一行（列）最大的数，然后如果对应列（行）并没有被删掉那么这里就有一个未确定元素，使用组合数合并一下即可。

这样只需要记录剩余行和列的个数，状态数 \(O(nm)\) 转移 \(O(1)\)，足以通过。

I. Maximum Subsequence

首先是一个 DP 套 DP 做法，很不幸的是其复杂度为 \(O(n 3^n)\)，我通过删掉被支配的元素成功通过了。[烟花][烟花][烟花] 大概就是说，我们记录已经加入的元素，记录每个最大后缀和能对应的最小最大子段和（已有的）。

而更加直接的做法是直接二分答案，因为历史信息并不需要求和，而是简单的不等式联立，可以做到 \(O(n 2^n \log V)\)，轻松通过本题。

J. Miner

注意到合法的 \(a\) 是连续的一段区间，使用点边容斥即可。