Tarjan再学习

蓝书的那一套理论比较生硬，且不是很深刻，故重学Tarjan。AlexWei《图论Ⅰ》

相关定义#

割点：在无向图中，删去使得连通分量数增加的点被称为割点。

割边：在无向图中，删去使得连通分量数增加的边被称为割边。

点双连通图：不存在割点的无向图。

边双连通图：不存在割边的无向图。

点双连通分量：一张图的极大点双连通子图称为点双连通分量（V-BCC），简称点双。

边双连通分量：一张图的极大边双连通子图称为边双连通分量（E-BCC），简称边双。

缩点：把一个连通分量等价为一个点的操作。边双和点双缩点后均得到一棵树，而强连通分量缩点后得到一张DAG。

基本性质#

边双连通#

考虑割边两侧的两个点 $u,v$。由于删去割边 $u,v$ 不连通，所以这条割边在任何一条 $u$ 到 $v$ 的迹上，否则删去后 $u,v$ 仍连通。

两点之间的所有必经边，就是连接它们所有迹的交。

在研究必经边时，重复经过一条边是不优的，所以只需考虑两点之间的迹（路径边集不重复）。

不难发现，割边和必经边的概念是完全等价的。$u,v$ 双连通当且仅当 $u,v$ 之间不存在必经边。

断开一条割边会使连通块数 +1。断开所有割边，每个连通块中不含割边且不能再扩大，是原图的边双连通分量。

这说明边双连通分量由割边连接，边双缩点得到一颗树，每条边都是原图割边。

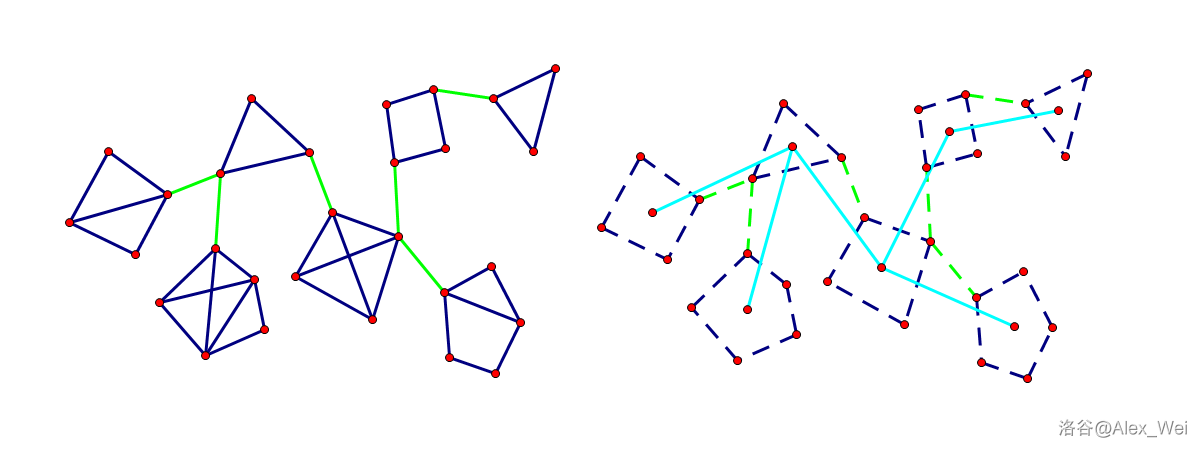
任意添加一条边 $(u,v)$，任意 $u,v$ 简单路径上的边不再是割边了，即该路径上的所有边双会被缩成一个大边双。

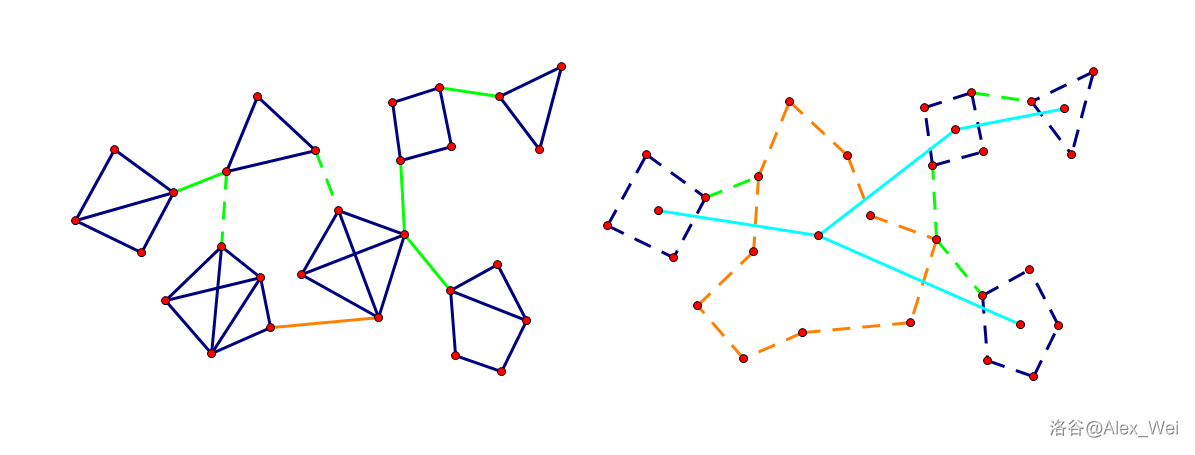
传递性：若 $u,v$ 双连通，$v,w$ 双连通，则 $u,w$ 双连通。

证明：$u,v$ 之间迹的交集为空（没有必经边），空集与空集取交还为空，因此 $u,w$ 之间没有必经边。

结论：边双的点集两两无交，每个点恰属于一个边双，根据传递性易证。

结论：对于边双内任意一条边 $(u,v)$，存在经过 $u,v$ 的回路；对于任意一点 $u$，存在经过 $u$ 的回路（除孤立点）。

证明：考虑边 $(u,v)$，将其删去后仍能得到一条 $u,v$ 的路径，将该路径与 $(u,v)$ 拼起来，即可得到穿过 $u,v$ 的回路。

点双连通#

与边双不同，两个点双可能有交，例如 "8字形"，中间的交点在两个点双都出现了。

因此点双不具有传递性。但如果两个点双有交，交点一定唯一，否则两个点双可以合并。

结论：若两点双有交，那么交点一定是割点。如果删去交点后两点双仍然连通，则可以合并。

引理：若两点点双连通，那么包含这两点的点双唯一。不唯一则出现两个交点，矛盾。

现在已经知道点双交点是割点，那么割点一定是点双交点吗？删去割点，考虑割点的两个邻居 $u,v$。

根据定义，$u,v$ 不连通，则 $u,v$ 不属于一个点双。

结论：一个点是割点当且仅当属于超过一个点双（上面充分性和必要性都有证明）。

结论：由一条边直接相连的两点点双连通。

推论：一条边恰属于一个点双。$(u,v)$ 连接的 $u,v$ 属于一个点双，如果他们同时属于另一个点双则产生矛盾。

正如割边是连接边双的「桥梁」，割点也是连接点双的桥梁。

用一个点代表一个点双，并将这个代表点向与之相连的割点连边，得到块割树。

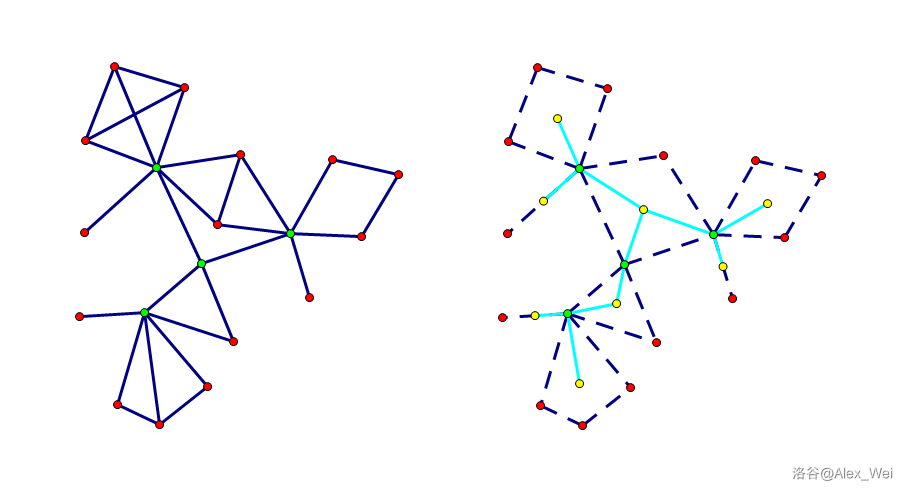
考虑删去点双中的一个点 $x$，剩下所有点连通。

如果度数大于 $1$，对于其不同的两个邻居 $u,v$，将新图中 $u,v$ 的路径与 $x$ 相连，得到经过 $x$ 的简单环。

若度数等于 $1$，则整个点双为"一边连两点"的平凡形态，即只可能在 $n=2$ 的时候出现。

如果 $n\ge 3$ 且存在 $d(u)=1$，设与其直接相连的唯一点为 $v$，删去 $v$ 后 $u$ 与整张图不连通，矛盾。

结论：对于 $n\ge 3$ 的点双中任意一点 $u$，存在经过 $u$ 的简单环。

Tarjan求割点#

无向图DFS树

给定无向连通图 $G$，从 $r$ 开始 dfs。取出进入每个点时的边 $(f{a}_i,i)$ 称为树边，其它为非树边，得到以 $r$ 为根的树。

无向图 DFS 树的性质：

• 祖先后代性：任意非树边两端具有祖先后代关系。
• 子树独立性：节点的每个儿子的子树之间没有边（和上一条性质等价）。
• 时间戳区间性：子树时间戳为一段连续区间。
• 时间戳单调性：节点的时间戳小于其子树内的时间戳。

后两点比较显然，证一下前两点，对于 $u$ 所有的出边 $v$：

$v$ 还没遍历到，未来一定在 $u$ 的子树中（不一定是儿子）；$v$ 已经被遍历到，$u$ 对于 $v$ 来说是没被遍历，$u$ 在 $v$ 的子树中。

非根节点的割点判定

记 $x$ 的子树 $T(x)$ 为 $x$ 在 DFS 树上的子树，记 $T(x{)}^{\prime }=V\setminus T(x)$，即整张图除 $T(x)$ 以外的部分。

设 $x$ 不为根，则 $T^{\prime }(x)\ne \mathrm{\varnothing }$，

删掉 $x$ 之后 $T(x{)}^{\prime }$ 通过树边相连仍然连通，若 $x$ 是割点则存在 $z\in T^{\prime }(x)$ 与 $y$ 不连通，显然 $y\in T(x)$。

由于 $y,z$ 不连通，$T^{\prime }(x)$ 连通，则 $y$ 与整个 $T^{\prime }(x)$ 不连通。反之如果存在 $y$ 与 $T^{\prime }(x)$ 不连通，$x$ 一定是割点。

条件等价于任意 $y\in T(x)$ 不经过 $x$ 能到达点均属于 $T(x)$。

如果 $y\in T(x)$ 不经过 $x$ 就与 $T^{\prime }(x)$ 连通，一定存在 $y$ 到 $v\in T^{\prime }(x)$ 的路径，使得 $v$ 是路径中第一个属于 $T^{\prime }(x)$ 的点。

设 $u$ 为路径中倒数第二个点，有 $u\in T(x)$。如果 $(u,v)$ 是树边，则 $u=x$，矛盾。

所以 $(u,v)$ 是非树边，$v$ 是 $u$ 的祖先，同理 $v$ 也是 $x$ 的祖先，一定有 $d_v<d_u$。

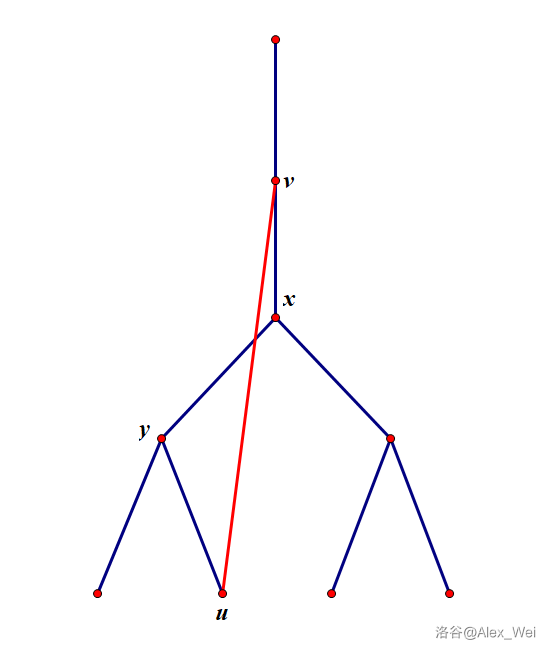
进一步的，由于 $x$ 的不同儿子之间没有非树边（子树独立性），设 $x$ 的儿子 $y^{\prime }$ 是 $y$ 的祖先，则 $u\in T(y^{\prime })$。

因此，如果 $y$ 能够不经过 $x$ 和 $T^{\prime }(x)$ 连通，则存在 $u\in T(y^{\prime })$ 满足 $u$ 有一条非树边与 $x$ 的祖先直接相连。

设 $f_x$ 表示 $x$ 通过非树边能（直接）到达的最小时间戳。

$x$ 不是割点的条件可以写成：对于任意儿子 $y^{\prime }$，都存在 $u\in T(y^{\prime })$，使得 $f_u<d_x$。

如果存在 $f_u<d_x$，$u$ 直接与 $T^{\prime }(x)$ 相连，$y^{\prime }$ 的其他点先通过树边先 $u$ 相连，再间接与 $T^{\prime }(x)$ 连通；

否则删掉 $x$ 后任意 $y^{\prime }$ 子树内的点都不与 $T^{\prime }$ 连通，$x$ 是割点。

得到非根节点的割点判定法则：如果存在儿子 $y^{\prime }$，使得 $\underset{u\in T(y^{\prime })}{min}{f}_u\ge d_x$，则 $x$ 是割点。

设 $g_x$ 表示 $x$ 子树内 $f_u$ 的最小值（low 数组的真正含义）：

$$\begin{array}{rl}{f}_x& =\underset{(x,y)\in E\wedge y\notin \text{son}(x)}{min}{d}_y\\ \\ g_x& =min(\underset{y\in \text{son}(x)}{min}{g}_y,f_x)\end{array}$$

当且仅当存在 $x$ 的儿子 $y$ 满足 $g_y\ge d_x$，$x$ 是割点。

根据上述 DP 的定义，$g_x$ 显然是初始化成 $inf$。当然初始化成 $d_x$ 也不会有错，代码上只是多一行少一行的区别。

根的割点判定法则

若 $x$ 在 DFS 树上有 $>1$ 个儿子，根据子树独立性，$x$ 的儿子两两不连通，$x$ 是割点。

如果 $x$ 只有一个儿子 $y$，删掉 $x$ 后 $T(y)$ 仍然连通，$x$ 不是割点。

割边求法#

Tarjan#

探究 $e=(u,v)$ 是割边的充要条件。

树边使整张图连通，割断非树边不影响连通性，因此 $e$ 是割边的一个必要条件是 $e$ 是树边。

不妨设 $v$ 是 $u$ 的儿子，如果割点 $e$ 后图不连通，只能分成 $T(v)$ 和 $T^{\prime }(v)$ 两部分，因为其内部都通过树边连通。

这说明 $T(v)$ 的所有节点都必须经过 $e$ 才能到达 $T^{\prime }(v)$。

如果存在 $w\in T(v)$，$w$ 能过通过一条非树边到达 $u$ 或其祖先，则 $e$ 不是割边，即 $\underset{w\in T(v)}{min}{f}_w=g_v\le d_u$。

割边判定法则：对于树边 $e=(u,v)$，$v$ 是 $u$ 的儿子，$e$ 是割边当且仅当 $g_v>d_u$。

树上差分#

已经知道树边是割边的一个必要条件。

如果存在非树边 $(u,v)$，那么搜索树上 $u\to v$ 的简单路径上所有树边都不是割边了。

怎么刻画一条树边有没有被非树边覆盖？把边 $(i,f{a}_i)$ 的覆盖次数当做 $i$ 的点权，树上差分后求子树和。

边双连通分量缩点#

由于每个点恰属于一个边双，把每个割边割断后剩下的每个连通块都是一个边双。

可以先 Tarjan 给所有割边打上标记，再 dfs 找连通分量，但太麻烦。

考虑原图的的 DFS 树，找到当前深度最深的一条割边 $(u,v)$，显然 $v$ 子树内没有割边，整个 $v$ 子树就是一个边双。

把 $v$ 及其子树删掉，递归此过程。具体实现可以访问一个点就把他压进栈，遇到割边 $(u,v)$ 则把栈顶到 $v$ 全部弹出。

最后栈内剩下一些点，组成一个包含根结点的边双，不要忘记弹出。

Caterpillar

如果图中存在环，这个环一定要缩成一个点。重边也可以规约为两条边的环。

不妨先用最小花费使整张图无环。如果 $u$ 还没有缩到所属边双中，一定还存在经过 $u$ 的环。

因此把 $u$ 缩到所属边双是必须的操作。

不会出现把 $u$ 缩到其他边双从而使操作数变小的情况，因为每个点恰属一个边双，必须操作数没变。

缩完点后得到一张森林，其中每棵树是独立的，最后把主链首尾相连即可。

对于一棵树，假如已经确定了主链，现在要在主链上挂尽可能多的点。

对于主链的一个分支，显然存在祖先后代关系的点不能同时挂在主链上，那么最优方案就是选该分支的所有叶子。

设整棵树有 $x$ 个叶子，主链长 $L$，主链两端一定是叶子，否则能继续延长。

操作次数为 $n-L-(x-2)$，$n,x$ 都是定值，最大化 $L$，取直径即可。submission