CSP2024-11 + 同余最短路
同余最短路
P3403 跳楼机
题意:给出正整数 \(x, y, z \le 10^5\) 和值域限制 \(h\),求 \(1 \sim h\) 中形如 \(ax + by + cz\) 的数的个数,其中 \(a, b, c\) 非负。
我们把最后答案根据模 \(c\) 分类:
那么对于每一个同余类 \(i\),问题转化为找 \(p = by + cz \equiv i \bmod c\) 的最小 \(p\)。
假设已经累加到了 \(v\),此时可以花费 \(y\) 到达 \((v + y) \bmod x\)。
所求的 \(p\) 就是起点到 \(i\) 的最短路。点数和边数都是 \(O(n)\),边权为正,dijstra 跑最短路。
[ABC077D] Small Multiple
题意:给定正整数 \(n\),求 \(n\) 的倍数中最小的数位和。
任意数可以被如下过程生成:
- \(+ 1\),同时数位和加一。
- \(\times 10\),数位和不变。
因此对模意义下的 \(n\) 个点连出两条边,\(+1\) 边权为 \(1\),\(\times 10\) 边权为 \(0\),01BFS 线性求最短路。
不会出现加一操作连续出现 10 次的情况,因为直接乘 10 代价更小。
P2662 牛场围栏
题意:给定 \(n\) 种长度的木棍(无限根),求出这些木棍不能拼出的最大长度。
取排序后最小的长度 \(a_1\) 为模数。
还是第一题的套路,求出与 \(i\) 同余的最小的 \(d_i = \sum_{j = 2}^{n} a_jx_j\) ,只不过这题每个点需要连出去 \(n - 1\) 条边。
时间复杂度 \(O(n^2\log n)\),对于每一种剩余类来说,其不能到达的最大长度等于 \(d_i - a_1\)。
P2371 [国家集训队] 墨墨的等式
题意:给定 \(n, [a_n], l, r\),求有多少 \(x \in [l, r]\) 使得 \(x = \sum a_ix_i\) 存在非负整数解。
还是套路,选最小的 \(a\) 作为模数,跑最短路,对每个剩余类依次考虑贡献。
P9140 [THUPC 2023 初赛] 背包
同余最短路的基本模型:选定基准物品作为模数 \(m\),对于每个 \(u \in [0, m)\),连边 \(x \xrightarrow{v_i} (x + v_i) \bmod m\)。
不转化为图论,本质是体积模 \(m\) 意义下的完全背包问题。
对于体积 \(v_i\) 的物品,它在长度为 \(m\) 的环上形成 \(\gcd(v_i, m)\) 个子环。
考虑证明:从 \(i\) 开始走,\(k\) 次后第一次回到 \(i\)(环长),即 \(i + kv \equiv i\) 的最小正整数解,环长 \(k = \frac{m}{\gcd(v, m)}\),共 \(\gcd(v, m)\) 个子环。
从一个点开始走,不可能绕着子环走一圈再回来。
从最短路的角度理解,一个点不会经过两次,否则出现负环;从背包的角度理解,走一圈会多 \(\frac{m}{\gcd(v, m)}\) 个代价,不如不走。
因此往背包加入体积为 \(v_i\) 的物品时,至多加入 \(\frac{m}{\gcd(v, m)} - 1\) 个。
对于每个子环,绕着这个环走两圈,因为只要两圈每个点都能转移到环上所有其他点。时间复杂度 \(O(nm)\)。
for(int k = 1; k <= n; ++ k) {
for(int i = 0, lim = __gcd(m, v[k]); i < lim; ++ i) { // 子环起点
for(int j = i, cnt = 0; cnt < 2; cnt += (j == i)) {
int p = (j + v[k]) % m;
f[p] = min(f[p], f[j] + v[k]), j = p;
}
}
}
同余最短路还在写最短路?感觉不如转圈!
回归本题。
题意:\(n\) 种物品,体积和价值分别为 \(v_i, c_i\),\(q\) 次询问,每次查询容量为 \(V\) 的背包能够是否能恰好装满,并最大化价值。
其中 \(n \le 50,\ v_i \le 10^5,\ c_i \le 10^6,\ q \le 10^5,\ 10^{11} \le V \le 10^{12}\)。
在完全背包可行性基础上加入权值维度。
选取 \(\dfrac{c_i}{v_i}\) 最大的物品作为基准,记 \(w = c_i, m = v_i\),为什么?因为 \(\dfrac{c_i}{v_i} \le \dfrac{w}{m}\),替代为同等体积的基准物品会比原方案更优。
对于一个询问 \(V\) 以及一组背包方案 \((V^\prime, C^\prime)\),满足 \(V^\prime \equiv V \pmod m\) 且 \(V^{\prime} \le V\),其价值等于 \(C^\prime + \dfrac{V - V^\prime}{m} \times w\)。
其中 \(\dfrac{V - V^\prime}{m} = \lfloor\dfrac{V}{m}\rfloor - \lfloor\dfrac{V^{\prime}}{m}\rfloor\)(因为两者同余)。问题转化为最大化 \(C - \lfloor\dfrac{V}{m}\rfloor \times w\)。
对于模 \(m\) 意义下的点 \(i\),考虑 \(i \to (i + v_k) \bmod m\) 的边权是什么。
对 \(C\) 的贡献显然是 \(c_k\),对 \(\lfloor\dfrac{V}{m}\rfloor\) 的贡献可以在数轴上理解:\(i\) 始终与真实体积同余,已经走到 \(i\),还需 \(m - i\) 才有 \(1\) 的贡献,因此新贡献等于 \(\lfloor\dfrac{i + v_k}{m}\rfloor\)。
CSP2024-11
A
大模拟,欠着。
B
题意:\(T\) 轮询问,每次给出 \(n, k\),问你长度为 \(n\) 的排列是否存在一个置换 \(f:[n] \to [n]\) 并且满足 \(f(i) \ne i\) 是得 \(k\) 次置换后回到原排列。
\(T \le 10^4,\ n \le 10^{18},\ k \le 10^{15}\),每个测试点保证不同的 \(k\) 最多 \(52\) 种。
\(i\) 向 \(f(i)\) 连边,得到若干长度大于 \(2\) 的环,最小正周期等于环长的最小公倍数。
由于最小公倍数要整除 \(k\),所有环长也要整除 \(k\)。
问题转化为 \(k\) 的非平凡因子组成的不定方程 \(\sum x_id_i = n\) 是否存在一组非负整数解。
由于任意因子都能被表示为其质因子的整数倍,实际只要判断 \(\sum x_ip_i = n\) 有没有非负整数解。
令 \(w(k)\) 表示本质不同质因子个数:
-
\(w(k) = 1\),只要判断是否有 \(p \mid n\)。
-
\(w(k) = 2\),拓展欧几里得 \(O(\log k)\) 求出特殊解,判断 \(x_1\) 为最小非负值时 \(x_2\) 是否非负。
-
否则做同余最短路,绕圈法的最坏复杂度等于 \(O\big(w(k)\sqrt[3]{k}\big)\)。
一个测试点不同 \(k\) 的个数很少,把询问离线,这样判断的复杂度是可接受的,瓶颈在于分解 \(k\)。
由于赛时肯定搓不出一个泼辣的肉,线性筛出 \(\sqrt k\) 内的质数。upd:线性筛没卡过。submission
C
题意:怎么出原啊?
Alice 和 Bob 在长度为 \(n\) 的棋盘上博弈,\(q\) 次询问,每次选出一个区间 \([l, r]\) 进行游戏。
从 \(l\) 开始,\(l\) 上的棋子减一,每步操作可以选择走到 \([i, i + m]\) 格,并使该位置棋子减一,不能操作则输。其中 \(n,q \le 4\times 10^5, m \le 10\)。
朴素 dp,\(f_i\) 表示 \(i\) 这格是否先手必胜:
\(f_i\) 只与 \(a_i\) 的奇偶性和右侧第一个 \(0\) 离 \(i\) 的距离有关(如果没有则距离等于 \(m + 1\))。
考虑线段树维护一个映射 \(f\),\(f(i)\) 表示右侧最近的 \(0\) 到 \(r\) 的距离为 \(i\) 时 \([l, r]\) 中最左侧的 \(0\) 到 \(l - 1\) 的距离。
如何合并区间 \(L, R\)?\(f(i) \gets f_L(f_R(i))\) 。
假设求出了询问区间 \([l, r]\) 的映射,Bob 获胜当且仅当 \(f_{[l, r]}(m + 1) = 1\)。
题目还要支持区间修改,由于答案只与奇偶性有关,可以一开始就对每个区间求出原来的和翻转后的映射,那么修改操作就直接看作区间翻转。
D
题意:\(n \times n\) 的棋盘上有 \(m\) 个矩形障碍。每次可以向右或向上,求 \((1, 1)\) 到 \((n, n)\) 本质不同的合法路径数。
两个路径本质不同当且仅当存在一个障碍,一条路径是从上面绕过去的,一条路径是总下面绕过去的。其中 \(n, m, \le 10^6\)。
如何计数才能不重不漏?
我们让每条路径向下,向右贴近障碍,使得「上 \(\to\) 右」操作只发生在障碍的转角,「上」操作只发生在障碍的左边界。
这样每条路径都是上阶梯型:
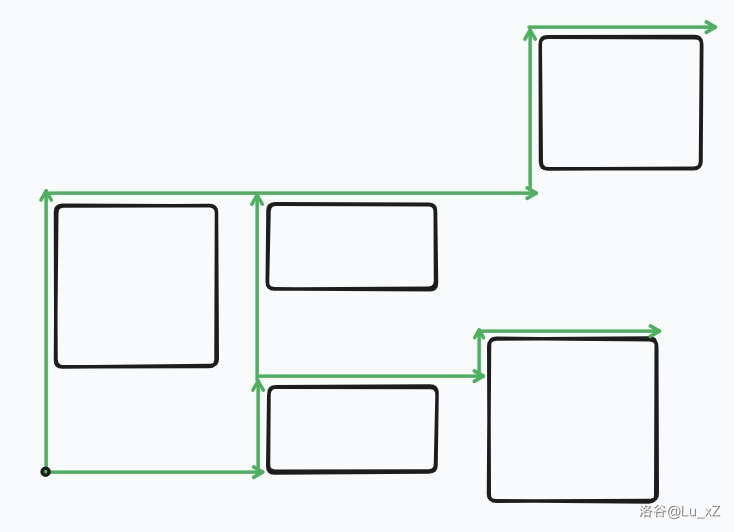
感性的理解一下为什么不重不漏,向下贴近不会改变路径与障碍的偏序关系,而向右贴近则使所有向上操作横坐标唯一确定。
\(f(x, y)\) 表示从 \((1, 1)\) 走到 \((x, y)\) 的本质不同路径数。
如果 \((x, y)\) 不是一个障碍的左上角,有平凡转移 \(f(x - 1, y) \to f(x, y)\)。
如果 \((x, y)\) 是一个障碍的左上角,除了平凡转移外还需考虑从 \(f(x - 1, < y)\) 转移。
假设红色是目标点 \((x, y)\),他可以从所有 \(f(x - 1, z)\) 转移,保证 \(z < y\) 且 \((x - 1, z)\) 到 \((x, y)\) 之间没有障碍。
问题转化到找最小的 \(z\) 使得 \((x - 1, z)\) 到 \((x, y)\) 没有障碍,然后用数据结构优化求和。
第一棵线段树维护当前横坐标的 dp 值,第二课线段树维护当前横坐标障碍的覆盖情况。
对于 \(f(x - 1, y) \to f(x, y)\) 的转移,直接继承 \(x - 1\) 的答案。
然后在第二棵线段树上从 \(y\) 开始二分最小的 \(z\),在第一棵线段树上求和,更新 \(y\) 的点值。
如果一个位置被障碍覆盖,那么该位置 dp 值为 \(0\)。
因此第一棵线段树还需支持区间清零,具体和第二棵的区间覆盖一起进行,在做第二种转移时特判掉左上角被覆盖的情况就行。
时间复杂度 \(O((n + m) \log n)\)。upd:不会树上二分,多了个 log,但是最优解?。submission


 浙公网安备 33010602011771号
浙公网安备 33010602011771号