2024“钉耙编程”中国大学生算法设计超级联赛（3）
死亡之组
如果 \(\sum [a_i < L] < 3\)，一定无解。
否则：
- \(a_1 < L\)，只需检验是否有 \(mx - mi > D\)，因为我们能同时选最大最小值。
- \(a_1 \ge L\)，此时不能选 \(mx\) 了，剩下的位置必须留给 \(a_1\)，检查是否 \(a_1 - mi > D\)。
code
#include<bits/stdc++.h>
#define eb emplace_back
#define ep emplace
using namespace std;
using ll = long long;
constexpr int N = 1e5 + 5;
int n, L, D, a[N];
void solve() {
cin >> n >> L >> D;
for(int i = 1; i <= n; ++ i) {
cin >> a[i];
}
int x = a[1];
sort(a + 1, a + n + 1);
int p = lower_bound(a + 1, a + n + 1, L) - a - 1;
int y = (x < L) ? a[n] : x;
if(p >= 3 && y - a[1] > D) {
cout << "Yes\n";
}
else {
cout << "No\n";
}
}
int main() {
cin.tie(0)->sync_with_stdio(0);
int T;
cin >> T;
while(T --) {
solve();
}
return 0;
}
深度自同构
设 \(n\) 个点可以组成 \(f_n\) 种树和 \(g_n\) 种森林。
森林中的每棵树必须形态相同，因此有 \(g_n = \sum\limits_{d \mid n} f_d\)。
树可以当做再 \(n - 1\) 的森林（或树）里加了一个点作为根，那么 \(f_n = f_{n - 1} + g_{n - 1}\)。
时间复杂度 \(O(n \ln n)\)。
code
#include<bits/stdc++.h>
using namespace std;
constexpr int N = 1e6 + 5, P = 998244353;
int n, f[N] = {1}, g[N];
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> n;
for(int i = 1; i <= n; ++ i) {
f[i] = (f[i - 1] + g[i - 1]) % P;
for(int j = i * 2; j <= n; j += i) {
g[j] = (g[j] + f[i]) % P;
}
}
for(int i = 1; i <= n; ++ i) {
cout << (f[i] + g[i]) % P << ' ';
}
return 0;
}
单峰数列
线段树裸题。
对于 \([l, r]\)，维护 \(\text{up, down, same, add}\) 以及 \(a_l, a_r\) \(6\) 个信息。
对于操作 \(5\)，二分出单峰的位置，然后检验另一侧是否符合条件，双 log 复杂度。
code
#include<bits/stdc++.h>
#define eb emplace_back
#define ep emplace
using namespace std;
using ll = long long;
constexpr int N = 1e5 + 5;
int n, m;
struct Node {
int same, up, dw;
ll l, r, add;
void pushup(const Node &a, const Node &b) {
l = a.l, r = b.r;
same = (a.same && b.same && a.l == b.l);
up = (a.up && b.up && a.r < b.l);
dw = (a.dw && b.dw && a.r > b.l);
}
void addtag(ll v) {
l += v, r += v, add += v;
}
} t[N << 2];
#define ls x << 1
#define rs ls | 1
void pushup(int x) {
t[x].pushup(t[ls], t[rs]);
}
void pushdown(int x) {
if(t[x].add) {
t[ls].addtag(t[x].add), t[rs].addtag(t[x].add);
t[x].add = 0;
}
}
void build(int x = 1, int l = 1, int r = n) {
if(l == r) {
int v; cin >> v;
t[x] = {1, 1, 1, v, v};
return;
}
int mid = l + r >> 1;
build(ls, l, mid), build(rs, mid + 1, r);
pushup(x);
}
void add(int L, int R, int v, int x = 1, int l = 1, int r = n) {
if(L <= l && r <= R) {
t[x].addtag(v);
return;
}
pushdown(x);
int mid = l + r >> 1;
if(L <= mid) add(L, R, v, ls, l, mid);
if(R > mid) add(L, R, v, rs, mid + 1, r);
pushup(x);
}
Node query(int L, int R, int x = 1, int l = 1, int r = n) {
if(L <= l && r <= R) return t[x];
pushdown(x);
int mid = l + r >> 1;
if(R <= mid) return query(L, R, ls, l, mid);
if(L > mid) return query(L, R, rs, mid + 1, r);
Node ret;
ret.pushup(query(L, R, ls, l, mid), query(L, R, rs, mid + 1, r));
return ret;
}
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> n, build();
cin >> m;
while(m --) {
int o, l, r; cin >> o >> l >> r;
if(o == 1) {
int v; cin >> v;
add(l, r, v);
continue;
}
int c = 0;
if(o != 5) {
Node x = query(l, r);
if(o == 2) c = x.same;
if(o == 3) c = x.up;
if(o == 4) c = x.dw;
}
else {
int tl = l, tr = r;
while(tl < tr) {
int mid = tl + tr + 1 >> 1;
(query(l, mid).up) ? tl = mid : tr = mid - 1;
}
if(tl == r || tl == l) c = 0;
else c = query(tl, r).dw;
}
cout << c << '\n';
}
return 0;
}
抓拍
\[C = 2 \times (\max x - \min x) + 2\times (\max y - \min y)
\]
手玩一下，\(\max x - \min x\) 的变化速度只可能是 \(-2, -1, 0, 1, 2\)，且一定按这个顺序（可能有些部分不存在）。
（我也不会严格证明，反正枚举几种情况就是凹的）
同理 \(\max y - \min y\) 也是关于时间 \(t\) 的凹函数。两个凹函数相加还是凹的，三分求极值点。
code
#include<bits/stdc++.h>
#define eb emplace_back
#define ep emplace
using namespace std;
using ll = long long;
constexpr int N = 2e5 + 5;
int n;
struct Node {
ll x, y; char o;
} a[N];
istream& operator >> (istream &in, Node &o) {
in >> o.x >> o.y >> o.o;
return in;
}
ll calc(int t) {
ll mxx = -1e18, mix = 1e18, mxy = -1e18, miy = 1e18;
for(int i = 1; i <= n; ++ i) {
auto [x, y, o] = a[i];
if(o == 'N') y += t;
if(o == 'S') y -= t;
if(o == 'E') x += t;
if(o == 'W') x -= t;
mxx = max(mxx, x), mix = min(mix, x);
mxy = max(mxy, y), miy = min(miy, y);
}
return 2 * (mxx - mix + mxy - miy);
}
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> n;
for(int i = 1; i <= n; ++ i) {
cin >> a[i];
}
int l = 0, r = 2e9;
while(l < r) {
int lmid = l + (r - l) / 3;
int rmid = r - (r - l) / 3;
if(calc(rmid) >= calc(lmid)) r = rmid - 1;
else l = lmid + 1;
}
cout << min(calc(l), calc(r));
return 0;
}
比特跳跃
考虑哪些跳跃操作是有用的（为方便表示，用 \(\mid\) 替代 \(\text{bitwise or}\)）。
如果从 \(y\) 跳到 \(x\) 且 \(y \notin x\)，由于 $ x \mid y \ge x \mid 1$，不会比从起点 \(1\) 跳到 \(x\) 更优。
但如果 \(y \in x\)，这一步的花费只有 \(kx\)，是有可能比 \(1 \to x\) 更优的。
直接的想法是 \(1\) 向所有 \(x\) 连 \(k\times (x \mid 1)\) 的边，\(x\) 的子集向 \(x\) 连 \(kx\) 的边，然后跑最短路。
但是这样空间和时间都不允许。
考虑优化连边过程（下图），每个点只与相差一位的点之间连边，新增边数降到 \(O(n \log n)\)。
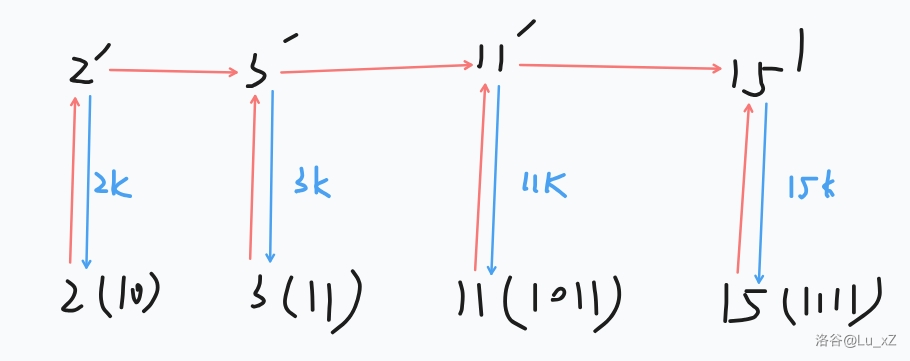
code
#include<bits/stdc++.h>
#define eb emplace_back
#define ep emplace
using namespace std;
using ll = long long;
void solve() {
int n, m, k, tot; cin >> n >> m >> k;
tot = 2 * n;
vector g(tot + 1, vector<pair<int, ll>>{});
for(int i = 1; i <= m; ++ i) {
int x, y, z; cin >> x >> y >> z;
g[x].eb(y, z);
g[y].eb(x, z);
}
for(int i = 2; i <= n; ++ i) {
g[1].eb(i, ll(i | 1) * k);
g[i].eb(i + n, 0), g[i + n].eb(i, (ll)k * i);
}
for(int i = 2; i <= n; ++ i) {
for(int j = 0; j < 20; ++ j) {
if(i >> j & 1) {
int k = i ^ (1 << j);
if(!k) continue;
g[k + n].eb(i + n, 0);
}
}
}
vector<int> v(tot + 1);
vector<ll> d(tot + 1, 1e18);
priority_queue<pair<ll, int>> q;
q.ep(d[1] = 0, 1);
while(!q.empty()) {
int x = q.top().second;
q.pop();
if(v[x]) continue;
v[x] = 1;
for(auto [y, z] : g[x]) {
if(d[y] > d[x] + z) {
d[y] = d[x] + z;
q.ep(-d[y], y);
}
}
}
for(int i = 2; i <= n; ++ i) cout << d[i] << " \n"[i == n];
}
int main() {
cin.tie(0)->sync_with_stdio(0);
int T;
cin >> T;
while(T --) {
solve();
}
return 0;
}
旅行
游走
游戏
记初始差值为 \(k\) 的数对 \((i, j)\) 个数为 \(b_k\)（\(a_i < a_j\)）
\[b_k = [x^k]\bigg( \sum c_ix^i \times \sum c_ix^{-i} \bigg)
\]
\(b_0\) 这样相乘会算重，直接算 \(\sum \begin{pmatrix} c_i\\2 \end{pmatrix}\)。
设在一轮中使 \((i, j)\) 差值减一，加一，不变的概率分别为 \(p_{-1}, p_1, p_0\)。（这里差值定义为 \(a_j - a_i\)）
记 \(m = \begin{pmatrix}n\\2\end{pmatrix}\)：
\[\begin{aligned}
p_{-1} &= p_1 = (n - 2) / m\\
\\
p_0 &= 1 - 2p_1
\end{aligned}
\]
构造多项式 \(F(x) =p_1x + \dfrac{p_{-1}}{x} + p_0\)，那么 \(t\) 轮之后 \((i, j)\) 相等的概率即 \([x^{-k}]F^t(x)\)。
把 \(F(x)\) 整体乘 \(x\)，\(F(x) = p_1x^2 + p_0x + p_{-1}\)，令 \(G(x) = F^t(x)\)。
\[\begin{aligned}
& G'(x) = tF^{t - 1}(x)\cdot F'(x)\\
\\
\implies & G'(x)\cdot F(x) = tG(x)\cdot F'(x)\\
\\
\implies & G'(x)\cdot (p_1x^2 + p_0x + p_{-1}) = G(x)\cdot (2tp_1x + tp_0)\\
\end{aligned}
\]
也就是 \(G\) 的第 \(i\) 项可以通过前几项递推过来。
具体的，设 \(g_i = [x^i]G(x)\)，对比两边的 \(i - 1\) 次项：
\[p_1\times (i - 2)\times g_{i - 2} + p_0 \times (i - 1) \times g_{i - 1} + p_{-1} \times i \times g_{i} = 2tp_1 \times g_{i - 2} + tp_0 \times g_{i - 1}
\]
移项，
\[i \times g_i = (2t - i + 2) \times g_{i - 2} + (t - i + 1)\times \frac {p_0}{p_{1}} \times g_{i - 1}
\]
答案为 \(\sum b_k \times g_{t - k}\)。
code
#include<bits/stdc++.h>
#define eb emplace_back
#define ep emplace
using namespace std;
using ll = long long;
constexpr int N = 3e6 + 5, V = 1e6;
constexpr int P = 998244353, tot = 1 << 21;
ll qpow(ll a, ll b = P - 2) {
ll c = 1;
while(b) {
if(b & 1) c = c * a % P;
b >>= 1;
a = a * a % P;
}
return c;
}
int n, t, rev[N], inv[10000005];
ll a[N], b[N], g[2];
ll c2(ll x) {return x * (x - 1) / 2 % P;}
void fft(ll *a, bool o = 1) {
for(int i = 0; i < tot; ++ i) {
if(i < rev[i]) {
swap(a[i], a[rev[i]]);
}
}
for(int mid = 1; mid < tot; mid *= 2) {
ll g1 = qpow(3, (P - 1) / (mid * 2));
if(!o) {
g1 = qpow(g1);
}
for(int i = 0; i < tot; i += mid * 2) {
ll gk = 1;
for(int j = 0; j < mid; ++ j, gk = gk * g1 % P) {
ll x = a[i + j], y = a[i + j + mid];
a[i + j] = (x + gk * y) % P;
a[i + j + mid] = (x - gk * y) % P;
}
}
}
if(o) return;
ll iv = qpow(tot);
for(int i = 0; i < tot; ++ i) a[i] = a[i] * iv % P;
}
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> n >> t;
for(int i = 1; i <= n; ++ i) {
int x; cin >> x;
++ a[x], ++ b[V - x];
}
ll s = 0;
for(int i = 1; i <= V; ++ i) s = (s + c2(a[i])) % P;
for(int i = 0; i < tot; ++ i) {
rev[i] = (rev[i / 2] / 2) | ((i & 1) << 20);
}
fft(a), fft(b);
for(int i = 0; i < tot; ++ i) a[i] = a[i] * b[i] % P;
fft(a, 0);
a[0] = s;
for(int i = 1; i < V; ++ i) a[i] = a[i + V];
ll im = qpow(c2(n));
ll p1 = (n - 2) * im % P, p0 = (1 - 2 * p1) % P;
g[0] = qpow(p1, t);
g[1] = t * p0 % P * qpow(p1, t - 1) % P;
inv[1] = 1;
for(int i = 2; i <= t; ++ i) {
inv[i] = -inv[P % i] * ll(P / i) % P;
}
ll ans = 0;
for(int i = 0; i <= 1; ++ i) {
int k = t - i;
if(k < V) ans = (ans + a[k] * g[i]) % P;
}
ll kk = p0 * qpow(p1) % P;
for(int i = 2; i <= t; ++ i) {
ll x = (2 * t - i + 2) * g[0] + (t - i + 1) * kk % P * g[1];
x = x % P * inv[i] % P;
int k = t - i;
if(k < V) ans = (ans + a[k] * x) % P;
g[0] = g[1], g[1] = x;
}
cout << (ans + P) % P;
return 0;
}
浙公网安备 33010602011771号